題目描述

對於剛上大學的牛牛來說，他面臨的第一個問題是如何根據實際情況申請合適的課程。

在可以選擇的課程中，有 2n2n 節課程安排在 nn 個時間段上。在第 ii（1 \leq i \leq n1≤i≤n）個時間段上，兩節內容相同的課程同時在不同的地點進行，其中，牛牛預先被安排在教室 c_ici​ 上課，而另一節課程在教室 d_idi​ 進行。

在不提交任何申請的情況下，學生們需要按時間段的順序依次完成所有的 nn 節安排好的課程。如果學生想更換第 ii節課程的教室，則需要提出申請。若申請通過，學生就可以在第 ii 個時間段去教室 d_idi​ 上課，否則仍然在教室 c_ici​ 上課。

由於更換教室的需求太多，申請不一定能獲得通過。通過計算，牛牛發現申請更換第 ii 節課程的教室時，申請被通過的概率是一個已知的實數 k_iki​，並且對於不同課程的申請，被通過的概率是互相獨立的。

學校規定，所有的申請只能在學期開始前一次性提交，並且每個人只能選擇至多 mm 節課程進行申請。這意味著牛牛必須一次性決定是否申請更換每節課的教室，而不能根據某些課程的申請結果來決定其他課程是否申請；牛牛可以申請自己最希望更換教室的 mm 門課程，也可以不用完這 mm 個申請的機會，甚至可以一門課程都不申請。

因為不同的課程可能會被安排在不同的教室進行，所以牛牛需要利用課間時間從一間教室趕到另一間教室。

牛牛所在的大學有 vv 個教室，有 ee 條道路。每條道路連線兩間教室，並且是可以雙向通行的。由於道路的長度和擁堵程度不同，通過不同的道路耗費的體力可能會有所不同。 當第 ii（1 \leq i \leq n-11≤i≤n−1）節課結束後，牛牛就會從這節課的教室出發，選擇一條耗費體力最少的路徑前往下一節課的教室。

現在牛牛想知道，申請哪幾門課程可以使他因在教室間移動耗費的體力值的總和的期望值最小，請你幫他求出這個最小值。

輸入輸出格式

輸入格式：

第一行四個整數 n,m,v,en,m,v,e。nn 表示這個學期內的時間段的數量；mm 表示牛牛最多可以申請更換多少節課程的教室；vv 表示牛牛學校裡教室的數量；ee表示牛牛的學校裡道路的數量。

第二行 nn 個正整數，第 ii（1 \leq i \leq n1≤i≤n）個正整數表示 c_ici​，即第 ii 個時間段牛牛被安排上課的教室；保證 1 \le c_i \le v1≤ci​≤v。

第三行 nn 個正整數，第 ii（1 \leq i \leq n1≤i≤n）個正整數表示 d_idi​，即第 ii 個時間段另一間上同樣課程的教室；保證 1 \le d_i \le v1≤di​≤v。

第四行 nn 個實數，第 ii（1 \leq i \leq n1≤i≤n）個實數表示 k_iki​，即牛牛申請在第 ii 個時間段更換教室獲得通過的概率。保證 0 \le k_i \le 10≤ki​≤1。

接下來 ee 行，每行三個正整數 a_j, b_j, w_jaj​,bj​,wj​，表示有一條雙向道路連線教室 a_j, b_jaj​,bj​，通過這條道路需要耗費的體力值是 w_jwj​；保證 1 \le a_j, b_j \le v1≤aj​,bj​≤v， 1 \le w_j \le 1001≤wj​≤100。

保證 1 \leq n \leq 20001≤n≤2000，0 \leq m \leq 20000≤m≤2000，1 \leq v \leq 3001≤v≤300，0 \leq e \leq 900000≤e≤90000。

保證通過學校裡的道路，從任何一間教室出發，都能到達其他所有的教室。

保證輸入的實數最多包含 33 位小數。

輸出格式：

輸出一行，包含一個實數，四捨五入精確到小數點後恰好22位，表示答案。你的輸出必須和標準輸出完全一樣才算正確。

測試資料保證四捨五入後的答案和準確答案的差的絕對值不大於 4 \times 10^{-3}4×10−3。 （如果你不知道什麼是浮點誤差，這段話可以理解為：對於大多數的演算法，你可以正常地使用浮點數型別而不用對它進行特殊的處理）

輸入輸出樣例

3 2 3 3
2 1 2
1 2 1
0.8 0.2 0.5 
1 2 5
1 3 3
2 3 1

2.80

說明

【樣例1說明】

所有可行的申請方案和期望收益如下表:

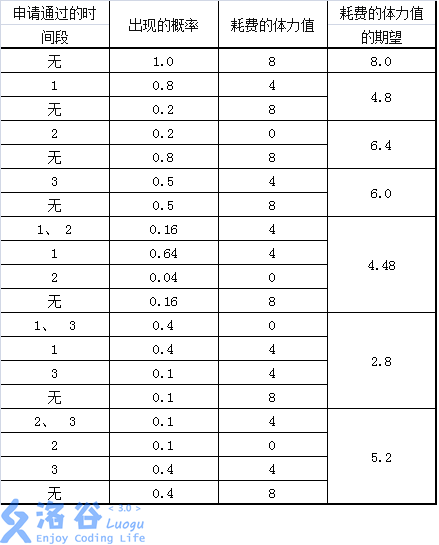
【提示】

1. 道路中可能會有多條雙向道路連線相同的兩間教室。 也有可能有道路兩端連線的是同一間教室。

2. 請注意區分n,m,v,e的意義, n不是教室的數量, m不是道路的數量。

   

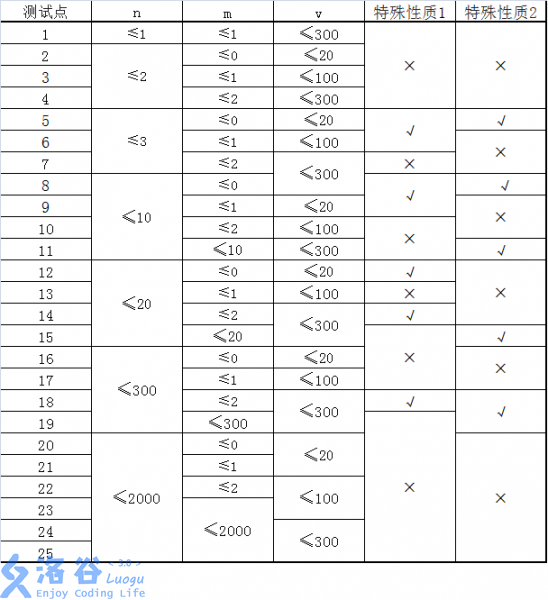
特殊性質1:圖上任意兩點 a_iai​, b_ibi​, a_iai​≠ b_ibi​間,存在一條耗費體力最少的路徑只包含一條道路。

特殊性質2:對於所有的 1≤ i≤ n1≤i≤n， k_i= 1ki​=1 。

題解

• 一開始顯然設dp[i][j]為走完前i個教室, 換了j次的最優方案
• 然後發現很難去轉移，因為不知道上一個教室的位置，也就是有沒有申請成功
• 所以可以改為dp[i][j][k]為走完前i個教室，換了j次，第i個教室我們有沒有選擇換教室的最優方案
• 首先，考慮不換的情況，也就是k=0
• dp[i][j][0]=min(dp[i][j][0],min(dp[i-1][j][0]+f[c[i-1]][c[i]],dp[i-1][j][1]+f[c[i-1]][c[i]]*(1-k[i-1])+f[d[i-1]][c[i]]*k[i-1]))
• 那麼這樣就有兩種情況了，①是i-1沒有換教室，那麼i是確定的，那麼只有一種可能就是f[c[i-1]][c[i]]
• ②是i-1換了教室，那麼i是確定的，那麼有兩種情況就是換成功了，和沒換成功，代價就是距離長度乘上概率
• 然後再考慮換的情況，也就是k=1

• dp[i][j][1]=min(dp[i][j][1],min(dp[i-1][j-1][0]+f[c[i-1]][c[i]]*(1-k[i])+f[c[i-1]][d[i]]*k[i],dp[i-1][j-1][1]+f[d[i-1]][d[i]]*k[i-1]*k[i]+f[d[i-1]][c[i]]*k[i-1]*(1-k[i])+f[c[i-1]][d[i]]*k[i]*(1-k[i-1])+f[c[i-1]][c[i]]*(1-k[i-1])*(1-k[i])))

• 其實就是跟上面類似
• ①i-1沒換
•       ⑴ i換成功了 ⑵ i沒換成功
• ②i-1也換
•      ⑴ i-1成功 i成功 ⑵ i-1成功 i不成功 ⑶ i-1不成功 i成功 ⑷ i-1不成功 i不成功
• 綜上所述，其實就是一道噁心的期望dp
• 還要記住，要用Floyd預處理最短距離（最短路）

程式碼

 1 #include <cstdio>
 2 #include <iostream>
 3 #include <cstring>
 4 using namespace std;
 5 const double inf=1e17+10;
 6 int n,m,v,e,c[2010],d[2010],f[310][310];
 7 double k[2010],dp[2010][2010][2],ans;
 8 int main()
 9 {
10     memset(f,63,sizeof(f));
11     scanf("%d%d%d%d",&n,&m,&v,&e);
12     for (int i=1;i<=n;i++) scanf("%d",&c[i]);
13     for (int i=1;i<=n;i++) scanf("%d",&d[i]);
14     for (int i=1;i<=n;i++) scanf("%lf",&k[i]);
15     for (int i=1,x,y,d;i<=e;i++) scanf("%d%d%d",&x,&y,&d),f[x][y]=f[y][x]=min(f[x][y],d);
16     for (int a=1;a<=v;a++)
17         for (int i=1;i<=v;i++)
18             for (int j=1;j<=v;j++)
19                 if (i!=j&&i!=a&&j!=a) f[i][j]=min(f[i][j],f[i][a]+f[a][j]);
20     for (int i=1;i<=v;i++) f[i][i]=0;
21     for (int i=0;i<=n;i++) for (int j=0;j<=m;j++) dp[i][j][0]=dp[i][j][1]=inf;
22     dp[1][0][0]=dp[1][1][1]=0;
23     for (int i=2;i<=n;i++)
24     {
25         dp[i][0][0]=dp[i-1][0][0]+f[c[i-1]][c[i]];
26         for (int j=1;j<=min(i,m);j++)
27         {
28             dp[i][j][0]=min(dp[i][j][0],min(dp[i-1][j][0]+f[c[i-1]][c[i]],dp[i-1][j][1]+f[c[i-1]][c[i]]*(1-k[i-1])+f[d[i-1]][c[i]]*k[i-1]));
29             dp[i][j][1]=min(dp[i][j][1],min(dp[i-1][j-1][0]+f[c[i-1]][c[i]]*(1-k[i])+f[c[i-1]][d[i]]*k[i],
30                             dp[i-1][j-1][1]+f[d[i-1]][d[i]]*k[i-1]*k[i]+f[d[i-1]][c[i]]*k[i-1]*(1-k[i])+f[c[i-1]][d[i]]*k[i]*(1-k[i-1])+f[c[i-1]][c[i]]*(1-k[i-1])*(1-k[i])));
31         }
32     }
33     ans=inf;
34     for (int i=0;i<=m;i++) ans=min(ans,min(dp[n][i][0],dp[n][i][1]));
35     printf("%.2lf",ans);
36 }