MATLAB數值法與微積分
阿新 • • 發佈:2018-11-12
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow
也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
第十二章 數值法與微積分
12.1 前言
函式之微分為求函式對自變數之導數,或為其斜率;利用數值方法則可以解出其他相關之問題,其應用部份已在前章討論。數值微分有兩種應用,其一是在資料收集完備後,分析其變化速度;其二為即時估計或量測速率。後者需要快速演演算法才能有立即反應。
計算斜率,依其定義即為dy/dx,在數值分析上必須轉化為可量測之變化量,亦即lim(Δy/Δx)。量取Δy或Δx則必須藉助前後之數值點,例如Δx=x2-x1=x3-x2等關係。但這樣總是會因Δx值之大小而有差異。此時之Δx值也不可能如理論之無限小值。在實際之計算上,取Δx之前、後或中就有向前差分、向後差分或中心差分之區別。
12.2 差分函式diff
12.2 差分函式diff
對於一個向量,差分函式在於求取該數列元素間之差異及其導數,相關指令格式如下:
Y = diff(X)
Y = diff(X,n)
Y = diff(X,n,dim)
若X為向量,則上述指令在於計算其相鄰元素間之差,亦即:
[X(2)-X(1) X(3)-X(2) ... X(n)-X(n-1)]
若X為矩陣,則結果將計算其相鄰列間之差,如:
[X(2:n,:) - X(1:n-1,:)].
引數n為階數,n=1時,其結果與Y = diff(X)相同,n=2時,其結果為diff(diff(X)),依此類推。因此每相差1其項數將減少一項。引數dim則是控制行向或列向差分,dim=1行向(預設值),dim=2為列向。
例:
>> x = 2:2:10
x =
2 4 6 8 10
>> y=diff(x)
y =
2 2 2 2
>> y=diff(x,2)
y =
0 0 0
若間矩較細,將過差分後,其結果應為原函式之導數。
h = .01;
x = 0:h:pi;
d=diff(sin(x.^2))/h;
plot(x,sin(x.^2),x,[0 d],'r:')

上例等於計算sin(x.^2)之導數 2*cos(x.^2).*x,注意d值之長度會比x少1。
例:
>>X=(1:10).^2,
X =
1 4 9 16 25 36 49 64 81 100
>>x1=diff(X),x2=diff(X,2), x3=diff(y)
x1 =
3 5 7 9 11 13 15 17 19
x2 =
2 2 2 2 2 2 2 2
x3 =
2 2 2 2 2 2 2 2
結果為x1比X少一項,x2比x1又少一項,x2與x3相同,證明y3=diff(diff(X))。
例:
X = [3 7 5 3; 2 0 8 4]
x1=diff(X,1), x2= diff(X,1,2)
X =
3 7 5 3
2 0 8 4
x1 =
-1 -7 3 1
x2 =
4 -2 -2
-2 8 -4
例:正弦函式sin(t)以常態分佈繪出[0 pi]間之區線及其第二導數cos(t)。
t=[0:pi/50:pi];nn=length(t);td=cos(t);
y=sin(t)+0.05*(randn(1,nn)-0.5);
dt1=diff(y)./diff(t);%backward(+)
dt2=(y(3:nn)-y(1:nn-2))./(t(3:nn)-t(1:nn-2));
plot(t,sin(t));hold on;plot(t,y,'b.');
plot(t,cos(t),'r:');
plot(t(1:nn-1),dt1,'k+');
plot(t(1:nn-2),dt2,'bo');
 '+':向後差分;'o'中央差分
'+':向後差分;'o'中央差分
由其結果比較,中央差分比向後差分之誤差為小。可由其與實際值之相關係數可以確定。就向後差分者,相關係數為0.4927;而中央差分則為0.7674。
[r1,p1]=corrcoef(t(1:nn-1),dt1)
[r2,p2]=corrcoef(t(1:nn-2),dt2)
r1 =
1.0000 -0.4927
-0.4927 1.0000
p1 =
1.0000 0.0003
0.0003 1.0000
r2 =
1.0000 -0.7674
-0.7674 1.0000
p2 =
1.0000 0.0000
0.0000 1.0000
由於diff之前減特質,所以其功能亦可用來決定某些向量之特性,例如屬增加序列或減少序列,或所謂之單向(monotonic)系列,或屬等距分佈之系列等。下面的例子可作為一般之應用:
- diff(x)==0 測試重複性之元素
- all(diff(x)>0) 測試其單向性
- all(diff(diff(x))==0) 測試各元素是否等距分佈
12.3 數值梯度gradient
12.3數值梯度gradient
一具有二自變數之函式F(x,y,z),其梯度之定義為:
▽F = (dF/dx)i +(dF/dy)j +(dF/dz)k
其計算之指令格式如下:
FX = gradient(F)
[FX,FY] = gradient(F)
[Fx,Fy,Fz,...] = gradient(F)
[...] = gradient(F,h)
[...] = gradient(F,h1,h2,...)
其中F為函式向量,切分後之間隔預設值為1,亦即h=1;若函式之變數增多,則h之值可因變數之不同另外設值。例如,h1可能屬於第一變數之區間;h2為第二變數之區間,而左邊之輸出值則依x,y,z之分量。
例一:
v=-2:0.2:2;
[x,y]=meshgrid(v);
z=x.*exp(-x.^2-y.^2);
[px,py]=gradient(z,.2,.2);
contour(z),hold on, quiver(px,py), hold off
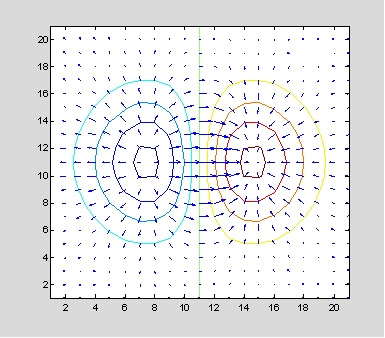
例二:
設有一向量F由魔術矩陣及巴斯上矩陣組成,其內容為:
>> F(:,:,1) = magic(3); F(:,:,2) = pascal(3);
>> F
F(:,:,1) =
8 1 6
3 5 7
4 9 2
F(:,:,2) =
1 1 1
1 2 3
1 3 6
取其梯度值,即▽F,設dx=1,dy=1,dz=1。則
>> gradient(F)
ans(:,:,1) =
-7 -1 5
2 2 2
5 -1 -7
ans(:,:,2) =
0 0 0
1.0000 1.0000 1.0000
2.0000 2.5000 3.0000
若間矩不同,即設dx=0.1,dy=0.1,dz=0.1。則▽F為
>> [PX,PY,PZ] = gradient(F,0.1,0.2,0.3)
PX(:,:,1) =
-70.0000 -10.0000 50.0000
20.0000 20.0000 20.0000
50.0000 -10.0000 -70.0000
PX(:,:,2) =
0 0 0
10.0000 10.0000 10.0000
20.0000 25.0000 30.0000
PY(:,:,1) =
-25.0000 20.0000 5.0000
-10.0000 20.0000 -10.0000
5.0000 20.0000 -25.0000
PY(:,:,2) =
0 5.0000 10.0000
0 5.0000 12.5000
0 5.0000 15.0000
PZ(:,:,1) =
-23.3333 0 -16.6667
-6.6667 -10.0000 -13.3333
-10.0000 -20.0000 13.3333
PZ(:,:,2) =
-23.3333 0 -16.6667
-6.6667 -10.0000 -13.3333
-10.0000 -20.0000 13.3333
12.4 Del2--Laplacian
Del2指令--非連續Laplacian
若U矩陣為一個函式u(x,y),其計算值係以該點之方格網路為基準,則4*del2(U)是拉普拉斯運算函式U之估計值,是以固定差分法估算的方式。亦即令:
L=▽²u/4 = (1/4)[d²u/dx² +d²u/dy²]
其中,
L(ij)= (1/4)[ui+1,j + ui-1,j +ui,j+ui,i+1+ui,j-1-ui-1,j-1
上述L矩陣與U同大小,其值為四個相鄰點平均值。上式若為三度空間,則除數4要改為6。計算上述函式之指令格式如下:
L = del2(U)
L = del2(U,h)
L = del2(U,hx,hy)
L = del2(U,hx,hy,hz,...)
其中U矩陣之每點之間隔為1,亦即h=1,若h之值不同於1,則另設其值。若U為兩維函式,則其在X與Y方向之間隔可用hx與hy另定,甚至三度空間也可加hz定義。
例:設U=x²+3y²,求其Laplacian向量
[x, y]=meshgrid(-4:4,-3:3);
U=x.*x+2*y.^2
V=4*del2(U)
U =
34 27 22 19 18 19 22 27 34
24 17 12 9 8 9 12 17 24
18 11 6 3 2 3 6 11 18
16 9 4 1 0 1 4 9 16
18 11 6 3 2 3 6 11 18
24 17 12 9 8 9 12 17 24
34 27 22 19 18 19 22 27 34
V =
6 6 6 6 6 6 6 6 6
6 6 6 6 6 6 6 6 6
6 6 6 6 6 6 6 6 6
6 6 6 6 6 6 6 6 6
6 6 6 6 6 6 6 6 6
6 6 6 6 6 6 6 6 6
6 6 6 6 6 6 6 6 6
12.5 多項式微分
多項式微分
多項式函式及多項數商等之導數可用polyder指令計算。其指令型式如下:
k = polyder(p)
k = polyder(a,b)
[q,d] = polyder(b,a)
polyder指令之輸入引數中,p,a,b等均為多項式係數之向量,以降冪排列。若僅有一個引數p,則k值為其導數。若是a,b兩輸入引數項,則表示為求a與b兩多項式之積之導數。若左邊有二個輸出引數(即[q,d])時,其計算方式是求多項數相除,即b/a之結果之導數,結果之分子置於q;分母置於d。
例如:有兩個多項式a=3x²+6x+9及b=2x+1,則其相乘積之導數可用下面之方式求得:
a=[3 6 9];b=[2 1];k=polyder(a,b)
k =
18 30 24
其導數之多項式為:18x²+30x+24
[k2,d]=polyder(a,b)
k2 =
6 6 -12
d =
4 4 1
此項之導數之多項式為: [6x²+6x-12]/ [4x²+4x+1]
12.6 一階微分方程之解法
12.6一階微分方程之解法
連續性函式之微分可以利用多種指令為之,而基本之細段微分法則是最早使用的概念,亦可利用MATLAB運算指令直接求解。
尤拉法(Euler method)
尤拉法為數值積分法最基本之一種。它是利用時間細段微分,利用初值及一階微分方程進行求解。以下列方程式為例:
y'=dy/dt = f(t,y)
式中t為時間,y為因變數。y', dy/dt 均為其一階微分的表示式。m為t之函式。根據微分之定義,可以改寫如下:
y'=dy/dt = limΔ-0 [y(t+Δt)-y(t)]/dt = f(t, y)
展開,可以求得經過Δt之時間後,y(t+Δt)之結果為:
y(t+Δt)=y(t)+Δtf(t,y)
若設Δt為一均勻之區段時間,或稱為步進值,則可以給予y(t)一個初值,然後利用增加步進值之個數逐步累積至最終的區間,最後得到y之答案值。其求解之型式如下:
y(tk+1) = y(tk) + Δtf(tk,y(tk))
故只要給定時間範圍及f(t0,y0)等初值,即可利用迴圈的方式得到最終答案。其中,Δt設定值之大小則會影響答案之準確度,Δt值愈大,準確度會差,Δt值愈小則運算時間加長。
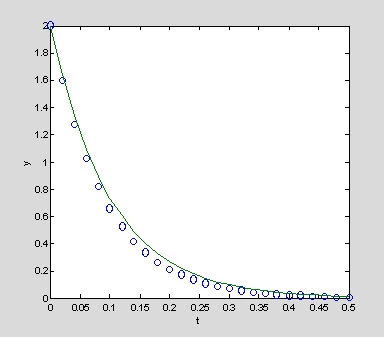
例:設f(t,y)=-10y,初值t=0, y0=2。且y'=-10y 之真實解為y(t)=2e -10t。設Δt=0.02,以此利用MATLAB求解。
function y=euler(y0,time,delta)
% Using Euler method to solve differential eqs.
% Inputs:
% y0:initial value
% time:time limit
% delta:step size
% Example: y=euler(2,0.5,0.02)
r=-10;k=0;
t=0:delta:time;y=zeros(size(t));
y(1)=y0;
for i=2:length(t),y(i)=y(i-1)+r*y(i-1)*delta;end
y_true=2*exp(-10*t);
plot(t,y,'o',t,y_true),xlabel('t'),ylabel('y');
執行結果:
>> y=euler(2,0.5,0.02);
同樣的問題亦可使用ode45指令計算,則先設定其函式為fun:
[email protected](t,y)(-10*y);
[t,y]=ode45(fun,[0 0.5],2);
plot(t,y,'ro',t,2*exp(-10*t)),xlabel('t'),ylabel('y');

利用MATLAB之ODE45之指令所得之結果比前面所用的方法準確度高。以下我們將介紹數種微分方程之解法及相關指令。
12.7初值型微分方程
12.7初值型微分方程
常微分方程式(Ordinary differential equations, ODE)為一般工數中求解的問題,包含有自變數與應變數,可以應用在多工程多方面動態之解析。若自變數增多,則成偏微分方程式,簡稱PDE(Partial differential equation)。目前MATLAB提供之微分方程解法器有數種,其效能及應用範圍略有不同。其中較常用的有ode23及ode45,這兩個均是利用Runge-Kutta法進行求解。其餘如ode113、ode15s、ode15i、ode23s、ode23t、ode23tb等等,其功能與範圍在運用上均有些差異,有些是根據不同方法得到的求解過程,常應用在控制方面。
常微分初值型解法器之相關函式均是利用數值積分方法作為求解過程。最初由設定之起始時間與條件,依設定之時間驅間逐步計算其解。若結果能滿足解法器設定之容許標準,就算成功;若無法達到,則必須再降低區間重新嚐試。常微分解法器之輸出入格式如下:
[t,Y] = solver(odefun,tspan,y0)
[t,Y] = solver(odefun,tspan,y0,options)
[t,Y,TE,YE,IE] = solver(odefun,tspan,y0,options)
sol = solver(odefun,[t0 tf],y0...)
上述指令中之solver,所指的就是ode45, ode23, ode113, ode15s, ode23s, ode23t, or ode23tb等等。其他相關引數介紹如下:
odefun:
用以計算微分方右邊之函式。所有解法器處理之系統方程式均是y'=dydt=f(t,y)之型式,有些是包括質量矩之問題,如M(t,y)y'=f(t,y)之函式。這些都與時間t有關,t為常數,而dydt及y均為行向量。ode45s解法器僅能處理質量為常數之問題;而ode15s與ode23t則能處理具奇數型質量矩陣之方程式,或稱為Differential-algebraic equations(DAEs)。
tspan 積分割槽間之向量[t0, tf]。解法器設定初值在tspan(1),然後由tspan(1)積分至tspan(end)。為得到特定時間(升冪或降冪)之對應解,可以使用tspan=[t0,t1, . . .,tf]。若tspan=[t0, tf],則會回應每個積分之步驟值。若tspan多於二個元素,則會回應時間對應值。時間必須依順序安排,或升冪或降冪。由於內部運算之安排,使用tspan向量之大小並不影響運算時間,但會佔據較多的記憶體。
y0:初值向量。
options:改變積分特性之相關引數。這些引數也可用odeset函式取得或設定。
輸出值包括t,Y,前者為時間點之行向量;後者為解答陣列,每一行之解y均與時間t相對應。每組(t,Y)之產生稱為事件函式。每次均會檢查是否函式等於零。並決定是否在零時終止運算。這可以在函式中之特性上設定。例如以events 或@events產生一函式。
[value, isterminal,direction]=events(t,y)
其中,value(i)為函式之值,isterminal(i)=1時運算在等於零時停止,=0時繼續;direction(i)=0時所有零時均需計算(預設值), +1在事件函式增加時等於零, -1在事件函式減少時等於零等狀況。
此外,TE, YE, IE則分別為事件發生之時間,事件發生時之答案及事件函式消失時之指標i。
有關初值型常微分方程之指令及其功能說明如下:
指令名稱 、說明及演算法:
- ode45 非剛性中階解法器 Runge-Kutta
- ode23 非剛性低階解法器 Runge-Kutta
- ode113 非剛性變階解法器 Adams
- ode15s 剛性變階解法器及 DAE NDFs (BDFs)
- ode23s 剛性低階解法器及 DAE Rosenbrock
- ode23t 中剛性梯形法則解法獸器及DAE Trapezoidal rule
- ode23tb 剛性低階解法器 TR-BDF2
ode45
此指令以 Runge-Kutta (4,5) 演演算法為基礎,運算上是屬單步驟計算y(t n),故僅需時間點前之解y(t n-1)。 ode45函式指令可作為第一階段評估的資料,然後再思考是否採取下一步驟。
ode23
與ode45函式同以 Runge-Kutta (2,3)方程式為基礎,並以Bogacki 與Shampine配對。在溫和剛性的情況,容許度較粗略時可能比ode45 更有效率。此指令也是單步驟解題。
ode15s
以數值微分方程(NDFs).為基礎之可變順序指令。可選擇後向微分方程BDFs, (或稱為Gear 法)。ode15s 是一個多步驟指令。若執行前認為問題特性屬於剛性,亦或使用過ode45 指令但無法達成目的時,可以試用f ode15s指令。
ode23s
以Rosenbrock修正方程式二階為基礎。. 由於它是單步驟解題指令,故在粗略容許範圍下可能比ode15s 更有效率。它可能解一些ode15s效率低或無法解的剛性問題。
ode23t
採用自由間極的梯形法。在問題屬於中等剛性或不需涵括數值阻尼的特性時可以使用此指令解題。
ode23tb
執行 TR-BDF2—初期利用梯形法涵蓋Runge-Kutta 方程式而第二階段採用後向微分法二階。 如同ode23s一樣,在粗略容許度下此法比ode15s有效率。
ODE 處理
積分指令之特性、引數可以藉ODE函式之處理而改變指令之內涵,並因而可以影響解題的結果:
函式名稱及說明
- odeset 設定或改變ODE指令之輸入選項
- odeget 取得odeset產生的選項特性
ODE 指令之輸出函式:
若輸出函式己經設定,則解題指令會在完成積分步驟後,呼叫這些特定函式。此時你可以使用odeset指令指定其中之一個樣本函式,作為OutputFcn 的特性,或你也可以加以修正,使其成為自已擁有的函式。
函式名稱及說明
- odeplot 時序圖
- odephas2 二維平面圖
- odephas3 三維相面圖
- odeprint 印出至指令窗
例:設一微分方程式為y'=sin(t),其初值y(0)=0,區間為 ,設其步進為週期(2π)之1/13,或者Δt=2π/13。其實際積分值為1-cos(t)。以尤拉法寫出之程式如下:
function y=euler2(y0,time,n)
% Using Euler method to solve differential eqs.
% y'=A*sin(t)
% Inputs:
% y0:initial value
% time:time limit,in the form of [t1 t2]*pi
% n:in the form of [1/n]*t2*pi, for step size
% Example: y=euler2(0,[0 2],13)
k=0;delta=time(2)/n;tt=time*pi;
t=tt(1):delta:tt(2);y=zeros(size(t));
y(1)=y0;
for i=2:length(t),
y(i)=y(i-1)+sin(t(i-1))*delta;
end
y_true=1-cos(t);
plot(t,y,'o',t,y_true),xlabel('t'),ylabel('y');
執行結果:
>>y=euler2(0,[0 4],13);
若改用ode45指令,其程式如下:
[email protected](t,y) sin(t);
[t,y]=ode45(fun,[0 4*pi],0);
plot(t,y,'ro',t,1-cos(t)),xlabel('t'),ylabel('y');
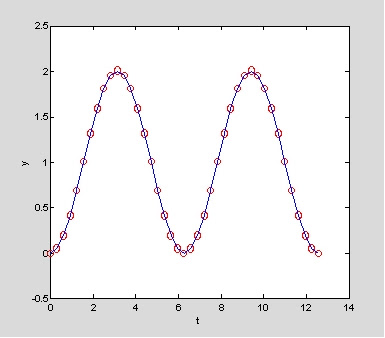
顯然利用ode45解法器比利用迴圈法為佳,當然迴圈法之Δt設定越小值,其準確度會趨近於後者之狀況。在上式之fun函式數,注意即使沒有y變數參與其中,也要將其列入,否則無法執行。
例:試解下面之微分方程式
10y' + y = te-2t y(0)=2; 0≦t≦2
並以其結果 y(t)=[732e -0.1t-19e -2t-10e -2t]/361比較之。
解:
[email protected](t,y) 0.1*(t*exp(-2*t)-y);
[t,y]=ode23(fun,[0 2],2);
y2=(732*exp(-0.1*t)-19*t.*exp(-2*t)-10*exp(-2*t))/361;
plot(t,y,'ro',t,y2),xlabel('t'),ylabel('y');
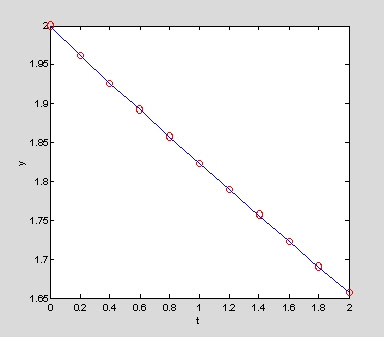
電路分析
例:一電路由一電阻器R與一電容器C串聯接於一電流v上,試求通過電容器兩端之端電壓y。
解:根據克希荷夫電壓定律總電壓為電流端電壓之和,故可建立如下之微分式:
RC[dy/dt]+y=v(t)
y(0)=2V RC=0.1s
由於開始時並無電源,故v=0。設時間常數RC=0.1s,經整理,其結果如次:
dy/dt =[v(t)-y]/0.1 = -10y
執行時,使用ode23解法器,一樣可獲得正確的結果。
[email protected](t,y) -10*y;
[t,y]=ode23(fun,[0, 0.4],2);
plot(t,y,'ro',t,2*exp(-10*t)),xlabel('t'),ylabel('y');

就所用點數而言,ode23解法器所用的點數較少。
由以上之範例可知,線性微分方程式均可使用數值法進行解析,雖然也有通用解可用,但大部份仍以數值法較為簡便。但若階數大於二時,使用通式會相當複雜,只有數值法可以解決,而且得到的結果可以立即用圖去表示,因而可以作比較。
若上例中之外在電壓有值,其型式為:
v(t) = 10et/Isin(2πt/p)
同樣,設 RC=0.1s,則前例仍可維持如下之型式:
dy/dt = 10[v(t)-y]
解法:
function y=euler3(y0,tf,tau,P)
% Using Euler method to solve differential eqs.
% RC(dy/dt)+y=v(t)
% Inputs:
% y0:initial value
% tf:time interval[t1 t2]
% tau, P:constants
% Example: y=euler3(0,[0 2],0.3,2)
[email protected](t) 10*exp(-t/tau).*sin(2*pi*t/P);
[email protected](t,y) 10*(vv(t)-y);
[t,y]=ode23(fun,tf,y0);
subplot(2,1,1)
plot(t,vv(t),'k-');xlabel('t'),ylabel('y');
subplot(2,1,2)
plot(t,y,'r-',t,y,'.');xlabel('t'),ylabel('y');
執行結果:
>>y=euler3(0,[0 2],0.3,2); %tau=0.3s, P=2s
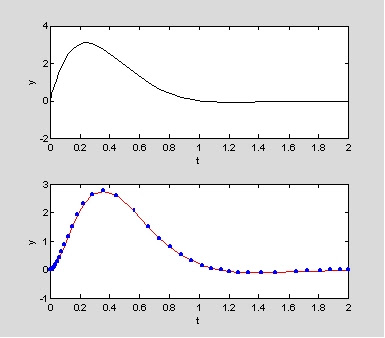
>>y=euler3(0,[0 0.2],0.05,0.03); %tau=0.05s, P=0.03s
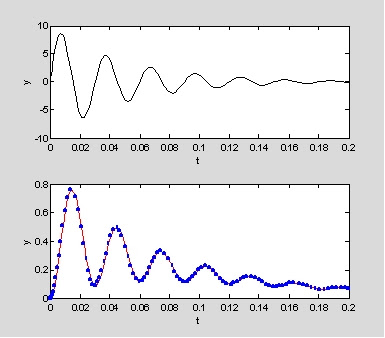
>>y=euler3(0,[0 0.8],0.3,0.03); %tau=0.3s, P=0.03s

12.8 非線性方程式解
12.8非線性方程式解
當常微分方程屬非線性時,就很難得到解析解,必須使用數值分析解。但這也常會發生一些垃圾答案的問題,必須就常識判斷其解之正當性。
例:有一大漏斗倉裝滿水,其外觀呈倒角錐形,半徑R高度為H,其體積為:
V=πR²H/3
倉體之上方,有一進水口,其流入速率為Qin;其底部則另有孔口流出。截面積為A,其流量Q與倉中之水位高度h有下列關係:
Q = Cd A (2gh)½
方程式中,Cd為孔口係數,其值為0.6。根據流體質量不滅的定理,倉中體積的變化應等於流體進出之流量,即:
dV/dt = Qin-Q
而由於r = (Rh/H),故:
dV/dt=d/dt[πr²dh/3]=πR²h²/(3H²]dh/dt , 故
[πR²h²/(3H²]dh/dt=Qin-Cd*A*(2gh) ½ 整理之,
dh/dt=[Qin-Cd*A*(2gh) ½]/[πR²h²/(3H²]
整理上面之公式寫成程式,並加以執行。
function [h,t]=tri_tank(tf,h0,R,H,cd,A,Qin)
% Using Euler method to solve differential eqs.
% Water tank
% Inputs:
% h0:initial water level
% tf:time interval[t1 t2]
% R,H:radius & height of tank, m
% cd:coefficient of orifice
% A: Crosssection of orifice, m^2
% Qin: Inlet flow, cms
% Example: h=tri_tank([0 10],9,10,9,0.6,1,10)
aa=3*(H/R)^2/pi;g=9.8;
[email protected](t,h) aa*(Qin-cd*A*sqrt(2*g*h));
[t,h]=ode23(vv,tf,h0);
plot(t,h,'r-',t,h,'.');xlabel('t'),ylabel('y');
執行結果:
>>hold on; for i=[5 7 10 15],h=tri_tank([0 10],9,10,9,0.6,1,i);end

圖中所示,由上而下分別為Qin=15, 10, 7, 5 cms。前兩者之水位高度會累積比初設值高,後二者因進水量較低,故會消耗一部份水量,最後在4米高時達到平衡。
高階微分方程式
解二階以上之微分方程式必須採用特定的方法。例如考慮二階微方如下:
5y"+7y'+4y = f(t)
先將其改寫為如下之型式以配合原來之一階微方:
y"=(1/5)f(t)-(4/5)y-(7/5)y'
此時因為右邊仍有一階微分項,為令其符合一階之格式,可以定義另外新變數x1及x2:
x1=y
x2=y'
根據此兩定義項,可以再進行微分一次,得到下面之等式:
x1'=y'
x2'=y"
將此代入上項微方,得聯立方程式:
x1'=x2
x2'=y"=(1/5)f(t)-(4/5)x1-(7/5)x2
此型式稱為柯西式(Cauchy form) 。設 f(t) = sin(t),其區間為0<t<6 ,並設起始條件y(0)=3,y'(0)=9,輸入初值因此為[3, 9]。則可以利用ode23解法器求得相關值。由於變數x1及x2可以置於同一矩陣中,其函式因此可以呼叫如下:
[email protected](t,x) [x(2);(1/5)*sin(t)-4*x(1)-7*x(2)];
[t,x]=ode23(fun,[0 6],[3 9]);
plot(t,x(:,1),'r-',t,x(:,2),'bo',t,x(:,2))
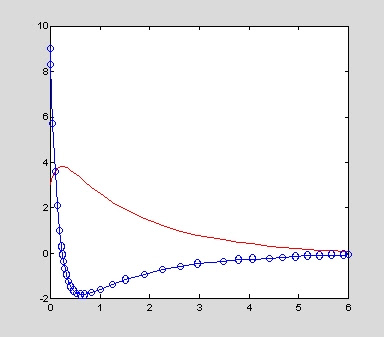
12.7 例項-剛性與非剛性問題
(編譯及圖示摘自mathworks.com)
簡單非剛性問題
MATLAB提供一個名為rigidode之程式是處理一剛性體體在無外在受力之情況下,所產生之速度與位移變化。這是一個由柯洛氏(Krogh)針對非剛性解法器提出的標準測試方法。其解析之答案屬於 Jacobian楕圓函式,可以由MATLAB中得到。其所用的區間約為1.5週期。其求解之聯立方程式如下:
為解此聯立微分方程,必須先建立包含這些方程式之函式,設為rigid,其中y為代表聯立方程式右邊之函式關係,為含有三元素之行向量,其內容如下:
function dydt = rigid(t,y)
dydt =[y(2) * y(3);-y(1) * y(3);-0.51 * y(1) * y(2)];
上述函式亦可利用隱函式表示,如下:
[email protected](t,y) [y(2) * y(3);-y(1) * y(3);-0.51 * y(1) * y(2)];
解法器可用ode45,其呼叫格式為:ode45(rigid,,),其中y0為初值,即為[0 1 1];tspan經歷時間,此處設為[0 12]。為方便起見,整個問題之定義及解題以M-檔存放。其微分方程則用次函式f表示。由於程式呼叫ode45 指令函式,沒有輸出項,故其輸出屬內定輸出函式odeplot,利用該函式直接將結果繪圖。
function rigidodex(tspan,y0)
% Solution of Euler's rigid body Equation
% revised from rigidode.m
% tspan: Interval, [t1, t2]
% y0: Initial value
%Example: rigidodex([0 12],[0 1 1])
y0 =y0(:);
[email protected](t,y) [y(2)*y(3);-y(1)*y(3);-0.51*y(1)*y(2)];
options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
[T,Y]=ode45(rigid,tspan,y0); % solve the problem using ODE45
plot(T,Y(:,1),'-',T,Y(:,2),'-.',T,Y(:,3),'.')
執行上述程式之結果如下圖:

剛性問題
凡德波(van der Pol)方程式屬一般剛性問題,其剛性用µ表示(本例之預設值設為µ=1000)。其微分聯立方程式如下:

在第二式中,當值增加,問題的本質會更顯出其剛性,此時擺動週期也隨之增大。當其值為1000時,擺動進入遲滯狀態,其剛性更強。在其限制的週期內有一部份解變化趨緩,然後反向迅速變化,呈現交替狀態。初期值則接近於變化緩慢之區域,以測試步距之大小。
為解上述聯立方程式,可先建立對應之函式vdp1000:
function dy = vdp1000(t,y)
dy = zeros(2,1); % a column vector
dy(1) = y(2);
dy(2) = 1000*(1 - y(1)^2)*y(2) - y(1);
對於剛性問題所用之ODE解法器係以採用近似Jacobian矩陣為主。為此通常可用odeset('Jacobian',@J)進行設定。其中J為次函式J(t,y,mu),屬於上項係數之偏微分矩陣,可求得點(t,y)附近具µ值之Jacobian 矩陣df/dx。
本例中,初值為[2 0],時間區間為[0 3000],使用ode15s解法器求解。
[T,Y] = ode15s(@vdp1000,[0 3000],[2 0]);
完整的程式如下:
function vdpodex(MU,y0)
% Solution of van der Pol Equation
% Example: vdpodex(500,[2 0])
if nargin==0,MU=1000;y0=[2 0];end
if nargin==1,;y0=[2 0];end
y0 =y0(:);tspan=[0; max(20,3*MU)];
[email protected](t,y,mu) [0 1;-2*mu*y(1)*y(2)-1 mu*(1-y(1)^2) ];
[email protected](t,y,mu) [y(2) ; mu*(1-y(1)^2)*y(2)-y(1) ];
options = odeset('Jacobian',J);
figure;
[t,y]=ode15s(f,tspan,y0,options,MU);
plot(t,y(:,1),'-o');
執行結果如下圖:

µ=1,並將繪圖指令改為:
plot(t,y(:,1),'-',t,y(:,2),'-.')
則上述程式執行後情況略有不同,其結果如下:
>>vdpodex(1,[2 1]) %設mu=1

具時間變數之微分方程
本例旨在解具有時間變數項之微分方程式。以下面之 ODE為例,其時間因變引數僅經由一系列之資料以兩向量型式決定:
y'(t) + f(t)y(t) = g(t)
式中之初值條件為 y(0) = 0,其中函式 f(t)定義為 n-x-1 向量 tf 與 f;而函式 g(t)則經過 m-x-1 向量 tg 與 g定義。
首先,與時間變化有關之引數 f(t)與 g(t)可以表示如下:
ft = linspace(0,5,25); % Generate t for f
f = ft.^2 - ft - 3; % Generate f(t)
gt = linspace(1,6,25); % Generate t for g
g = 3*sin(gt-0.25); % Generate g(t)
寫出 M-檔案函式程式就上述之指定值進行內插,以求得特定時間點之時變對應值。
function dydt = myode(t,y,ft,f,gt,g)
f = interp1(ft,f,t); % Interpolate the data set (ft,f) at time t
g = interp1(gt,g,t); % Interpolate the data set (gt,g) at time t
dydt = -f.*y + g; % Evalute ODE at time t
其次,利用ode45解法器中之引數呼叫上述之導數函式 myode.m :
Tspan = [1 5]; % Solve from t=1 to t=5
IC = 1; % y(t=0) = 1
[T Y] = ode45(@(t,y) myode(t,y,ft,f,gt,g),TSPAN,IC); % Solve ODE
繪出 y(t)解與時間之函式關係:
plot(T, Y);
title('Plot of y as a function of time');
xlabel('Time'); ylabel('Y(t)');

12.9矩陣解法
12.9矩陣解法
柯西型是高階微分方程之解法,但也可配合矩陣的型式求解。利用矩陣時,可以先以eig函式求其特徵值(eigen value),以確定其根及時間常數,其時間常數則為特徵根之負倒數。利用時間常數可以估計函式達到穩定狀態所需之時間。
以直流馬達之應用為例,電樞與電感L、電阻器R,共同串聯於一直流電壓之中如下圖,電樞則因扭力、慣性力及阻尼等達到動力平衡。
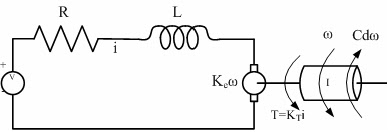
L(di/dt) = -Ri - Keω+v(t)
I(dω/dt)=KTi-Cdω
其中,L、R、I分別代表馬達的電感、電阻及電樞之轉動慣量,而Kt、Ke、Cd分別為力矩常數、反電動勢及阻尼係數。將上述聯立微分方程式改為柯西式,並設 x 1=i, x 2=ω,以此代入上式,並改寫矩陣型式:[X']=[A][X]+[1/L; 0]v(t),其中
[X]=
x1
x2
[X']=
x'1
x'2
[A]=
-R/L -Ke/L
KT/I -Cd/I
設直流電壓v為一控制馬達的因子,利用電壓之變化可以將馬達加速到穩定的速度。經過一段時間運轉後,再減電壓,使電樞減速並至停止。
在解法器所需之函式中,其表示法除常用的匿函式外,亦可使用其他型式之函式。匿函式最大的優點可以在主程式中共享變數資源,但其形成必須濃縮在一行之中,有時無法表達所有資訊,故仍然必須藉助次函式或巢狀函式。巢狀函式是將函式包藏在主函式之中,可供主函式直接呼叫,也可以共用主函式內之變數。茲將上式改寫為程式,其結果如下:
function motor(R,L,Cd,I,Kt,Ke,Tc)
% Calculate the voltage & velocity of motor
% R:resistor, ohms
% L:Inductance, H
% Cd: Coef of Damping of armature
% Kt: Torque constant N.m/A
% Ke: counter emf, V
% I: moment of inertia, kg.m^2
% Tc:control points for voltage=[t1 t2 tf]
% Example:
% motor(0.6,0.002,0,6e-5,0.04,0.04,[0.1 0.4 0.5])
A=[-R/L, -Ke/L;Kt/I, -Cd/I];B=[1/L; 0];
function v=volt(t)
v=zeros(size(t));
a=t<=Tc(3) & t>Tc(2); v(a)=-100*(t(a)-Tc(3));
b=t<=Tc(2) & t>Tc(1); v(b)=10;
v(t<Tc(1))=100*t(t<Tc(1));
end
[email protected](t,x) A*x+B*volt(t);
[t,x]=ode23(xdot,[0 0.6],[0 0]);
subplot(3,1,1)
plot(t,volt(t));xlabel('t(s)');ylabel('Voltage,V');
subplot(3,1,2)
plot(t,x(:,2),'k-');xlabel('t(s)');ylabel('Ang
