3.骰子塗色（UVA253）利用旋轉矩陣求解

• 題目簡單分析
• 程式碼

題目簡單分析

題目的詳細內容可以在這個網站上看到，下面簡單說明一下題目要求。
[題意]
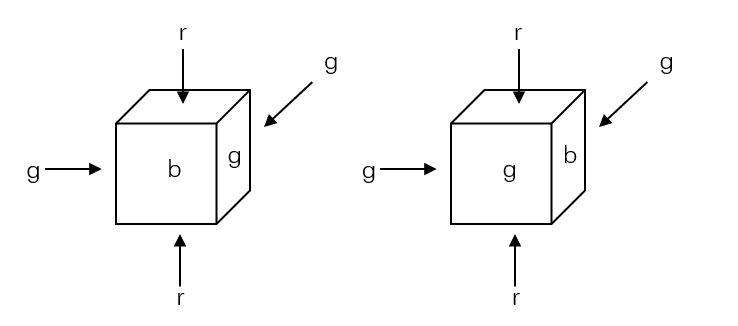
本題給出兩顆六面塗色（r、g、b三種顏色）的骰子。需要解決的問題是判斷其中一顆骰子能否通過旋轉得到另一顆骰子。

[輸入輸出]
樣例輸入如下：每行給出12個字元，前6個字元和後6個字元分別是兩顆骰子的塗色（按照下圖順序排列）。

程式只需要輸出判斷的結果即可（TRUE/FALSE）。
Sample Input

rbgggrrggbgr
rrrbbbrrbbbr
rbgrbgrrrrrg

Sample Output

TRUE
FALSE
FALSE

[分析]
本題主要解決的問題是骰子的旋轉，可以通過固定一個軸，列舉可能的情況來對所有情況進行判斷，網上已經又許多類似的解法了。這裡我通過矩陣的方法來模擬骰子的旋轉，可以通過旋轉矩陣求解得出所有的結果，然後將求解的結果與另一顆骰子的顏色進行比較得出結果。下面是分別繞三個軸進行旋轉的矩陣：

將三個矩陣相乘可以得到如下矩陣（注意矩陣為左乘，這裡採用了3-1-2尤拉角的形式）：

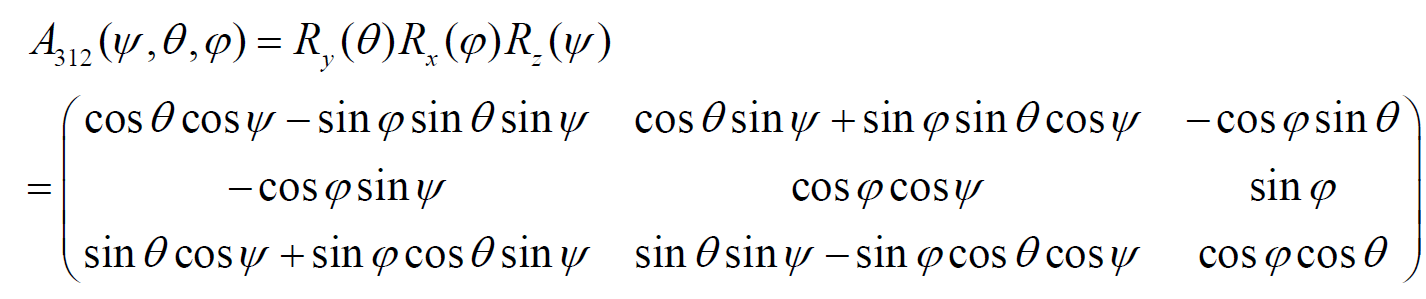
將旋轉矩陣作用於骰子的姿態矩陣，可以得到骰子旋轉之後的姿態；通過遍歷各個旋轉角度得到骰子可能的旋轉結果，然後將旋轉結果與另一枚骰子進行比較，如果相同則說明兩枚骰子的塗色是相同的，否則塗色不同。

程式碼

程式碼中需要注意的有以下幾點：
1.由於旋轉的角度為90度的整數倍，可以通過自定義三角函式來減少計算複雜度。
2.需要自定義矩陣乘法
3.骰子的塗色與姿態矩陣之間的轉換
完整程式碼如下，用C語言實現，VS2017的工程在github。程式碼如有bug，敬請指出。

#include <stdio.h>
#include <string.h>
char temp[12];
char a[6], b[6];//儲存輸入
int R[3][3];//旋轉矩陣
int Sin(int a);
int Cos(int a);
void updateR(int pitch,
 
 int roll, int yaw);
void Rotate(char c[6]);
int main() {
	int flag = 0;
	while (scanf("%s", temp) != EOF) {
		memcpy(b, temp + 6, 6 * sizeof(char));
		flag = 0;
		for (int i = 0; i < 360; i += 90)
			for (int j = 0; j < 360; j += 90)
				for (int k = 0; k < 360; k += 90) {
					memcpy(a, temp, 6 * sizeof(char));
					updateR(i, j, k);
					Rotate(a);
					if (strcmp(a, b) == 0) {
						flag = 1;i = j = k = 360;
					}
				}
		if (flag) printf("TRUE\n");
		else printf("FALSE\n");
	}
	return 0;
}
void Multi(int r[3][3], int m[3][6], int a[3][6]) {//矩陣乘法
	for (int i = 0; i < 3; ++i)
		for (int j = 0; j < 6; ++j) {
			a[i][j] = r[i][0] * m[0][j] + r[i][1] * m[1][j] + r[i][2] * m[2][j];
		}
}
void Rotate(char c[6]) {//旋轉
	int Mat[3][6] = { 0 }, Ret[3][6] = { 0 };
	//向量轉矩陣
	Mat[2][0] = c[0]; Mat[0][1] = c[1]; Mat[1][2] = -c[2];
	Mat[1][3] = c[3]; Mat[0][4] = -c[4]; Mat[2][5] = -c[5];
	//旋轉矩陣作用於矩陣
	Multi(R, Mat, Ret);
	for (int i = 0; i < 6; ++i) {
		if (Ret[2][i] > 0) c[0] = Ret[2][i];
		else if (Ret[0][i] > 0) c[1] = Ret[0][i];
		else if (Ret[1][i] < 0) c[2] = -Ret[1][i];
		else if (Ret[1][i] > 0) c[3] = Ret[1][i];
		else if (Ret[0][i] < 0) c[4] = -Ret[0][i];
		else if (Ret[2][i] < 0) c[5] = -Ret[2][i];
	}
}
void updateR(int pitch, int roll, int yaw) {//更新旋轉矩陣
	//3-1-2旋轉矩陣（Z-X-Y）
	R[0][0] = Cos(pitch)*Cos(yaw) - Sin(roll)*Sin(pitch)*Sin(yaw);
	R[0][1] = Cos(pitch)*Sin(yaw) + Sin(roll)*Sin(pitch)*Cos(yaw);
	R[0][2] = -Cos(roll)*Sin(pitch);
	R[1][0] = -Cos(roll)*Sin(yaw);
	R[1][1] = Cos(roll)*Cos(yaw);
	R[1][2] = Sin(roll);
	R[2][0] = Sin(pitch)*Cos(yaw) + Sin(roll)*Cos(pitch)*Sin(yaw);
	R[2][1] = Sin(pitch)*Sin(yaw) - Sin(roll)*Cos(pitch)*Cos(yaw);
	R[2][2] = Cos(roll)*Cos(pitch);
}
//為了簡化三角運算，自定義三角函式如下
int Sin(int a) {//a的取值應為0、90、180、270
	if (a == 90) return 1;
	else if (a == 270) return -1;
	else return 0;
}
int Cos(int a) {//a的取值應為0、90、180、270
	if (a == 0 || a == 360) return 1;
	else if (a == 90 || a == 270) return 0;
	else return -1;
}