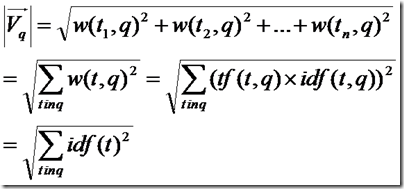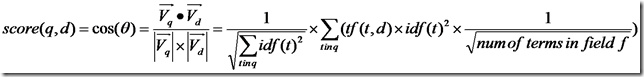Lucene打分公式的數學推導
在進行Lucene的搜尋過程解析之前,有必要單獨的一張把Lucene score公式的推導,各部分的意義闡述一下。因為Lucene的搜尋過程,很重要的一個步驟就是逐步的計算各部分的分數。
Lucene的打分公式非常複雜,如下:
在推導之前,先逐個介紹每部分的意義:
- t:Term,這裡的Term是指包含域資訊的Term,也即title:hello和content:hello是不同的Term
- coord(q,d):一次搜尋可能包含多個搜尋詞,而一篇文件中也可能包含多個搜尋詞,此項表示,當一篇文件中包含的搜尋詞越多,則此文件則打分越高。
- queryNorm(q):計算每個查詢條目的方差和,此值並不影響排序,而僅僅使得不同的query之間的分數可以比較。其公式如下:
- tf(t in d):Term t在文件d中出現的詞頻
- idf(t):Term t在幾篇文件中出現過
- norm(t, d):標準化因子,它包括三個引數:
- Document boost:此值越大,說明此文件越重要。
- Field boost:此域越大,說明此域越重要。
- lengthNorm(field) = (1.0 / Math.sqrt(numTerms)):一個域中包含的Term總數越多,也即文件越長,此值越小,文件越短,此值越大。
- 各類Boost值
- t.getBoost():查詢語句中每個詞的權重,可以在查詢中設定某個詞更加重要,common^4 hello
- d.getBoost():文件權重,在索引階段寫入nrm檔案,表明某些文件比其他文件更重要。
- f.getBoost():域的權重,在索引階段寫入nrm檔案,表明某些域比其他的域更重要。
以上在Lucene的文件中已經詳細提到,並在很多文章中也被闡述過,如何調整上面的各部分,以影響文件的打分,請參考有關Lucene的問題(4):影響Lucene對文件打分的四種方式一文。
然而上面各部分為什麼要這樣計算在一起呢?這麼複雜的公式是怎麼得出來的呢?下面我們來推導。
首先,將以上各部分代入score(q, d)公式,將得到一個非常複雜的公式,讓我們忽略所有的boost,因為這些屬於人為的調整,也省略coord,這和公式所要表達的原理無關。得到下面的公式:
然後,有Lucene學習總結之一:全文檢索的基本原理中的描述我們知道,Lucene的打分機制是採用向量空間模型的:
我們把文件看作一系列詞(Term),每一個詞(Term)都有一個權重(Term weight),不同的詞(Term)根據自己在文件中的權重來影響文件相關性的打分計算。
於是我們把所有此文件中詞(term)的權重(term weight) 看作一個向量。
Document = {term1, term2, …… ,term N}
Document Vector = {weight1, weight2, …… ,weight N}
同樣我們把查詢語句看作一個簡單的文件,也用向量來表示。
Query = {term1, term 2, …… , term N}
Query Vector = {weight1, weight2, …… , weight N}
我們把所有搜尋出的文件向量及查詢向量放到一個N維空間中,每個詞(term)是一維。
我們認為兩個向量之間的夾角越小,相關性越大。
所以我們計算夾角的餘弦值作為相關性的打分,夾角越小,餘弦值越大,打分越高,相關性越大。
餘弦公式如下:
下面我們假設:
查詢向量為Vq = <w(t1, q), w(t2, q), ……, w(tn, q)>
文件向量為Vd = <w(t1, d), w(t2, d), ……, w(tn, d)>
向量空間維數為n,是查詢語句和文件的並集的長度,當某個Term不在查詢語句中出現的時候,w(t, q)為零,當某個Term不在文件中出現的時候,w(t, d)為零。
w代表weight,計算公式一般為tf*idf。
我們首先計算餘弦公式的分子部分,也即兩個向量的點積:
Vq*Vd = w(t1, q)*w(t1, d) + w(t2, q)*w(t2, d) + …… + w(tn ,q)*w(tn, d)
把w的公式代入,則為
Vq*Vd = tf(t1, q)*idf(t1, q)*tf(t1, d)*idf(t1, d) + tf(t2, q)*idf(t2, q)*tf(t2, d)*idf(t2, d) + …… + tf(tn ,q)*idf(tn, q)*tf(tn, d)*idf(tn, d)
在這裡有三點需要指出:
- 由於是點積,則此處的t1, t2, ……, tn只有查詢語句和文件的並集有非零值,只在查詢語句出現的或只在文件中出現的Term的項的值為零。
- 在查詢的時候,很少有人會在查詢語句中輸入同樣的詞,因而可以假設tf(t, q)都為1
- idf是指Term在多少篇文件中出現過,其中也包括查詢語句這篇小文件,因而idf(t, q)和idf(t, d)其實是一樣的,是索引中的文件總數加一,當索引中的文件總數足夠大的時候,查詢語句這篇小文件可以忽略,因而可以假設idf(t, q) = idf(t, d) = idf(t)
基於上述三點,點積公式為:
Vq*Vd = tf(t1, d) * idf(t1) * idf(t1) + tf(t2, d) * idf(t2) * idf(t2) + …… + tf(tn, d) * idf(tn) * idf(tn)
所以餘弦公式變為:
下面要推導的就是查詢語句的長度了。
由上面的討論,查詢語句中tf都為1,idf都忽略查詢語句這篇小文件,得到如下公式
所以餘弦公式變為:
下面推導的就是文件的長度了,本來文件長度的公式應該如下:
這裡需要討論的是,為什麼在打分過程中,需要除以文件的長度呢?
因為在索引中,不同的文件長度不一樣,很顯然,對於任意一個term,在長的文件中的tf要大的多,因而分數也越高,這樣對小的文件不公平,舉一個極端的例子,在一篇1000萬個詞的鴻篇鉅著中,"lucene"這個詞出現了11次,而在一篇12個詞的短小文件中,"lucene"這個詞出現了10次,如果不考慮長度在內,當然鴻篇鉅著應該分數更高,然而顯然這篇小文件才是真正關注"lucene"的。
然而如果按照標準的餘弦計算公式,完全消除文件長度的影響,則又對長文件不公平(畢竟它是包含了更多的資訊),偏向於首先返回短小的文件的,這樣在實際應用中使得搜尋結果很難看。
所以在Lucene中,Similarity的lengthNorm介面是開放出來,使用者可以根據自己應用的需要,改寫lengthNorm的計算公式。比如我想做一個經濟學論文的搜尋系統,經過一定時間的調研,發現大多數的經濟學論文的長度在8000到10000詞,因而lengthNorm的公式應該是一個倒拋物線型的,8000到 10000詞的論文分數最高,更短或更長的分數都應該偏低,方能夠返回給使用者最好的資料。
在預設狀況下,Lucene採用DefaultSimilarity,認為在計算文件的向量長度的時候,每個Term的權重就不再考慮在內了,而是全部為一。
而從Term的定義我們可以知道,Term是包含域資訊的,也即title:hello和content:hello是不同的Term,也即一個Term只可能在文件中的一個域中出現。
所以文件長度的公式為:
代入餘弦公式:
再加上各種boost和coord,則可得出Lucene的打分計算公式。