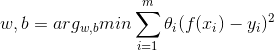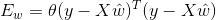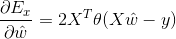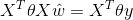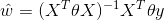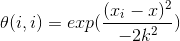區域性加權線性迴歸

線性迴歸的一個問題是有可能出現欠擬合，因為它求的是具有最小均方誤差的無偏估計，顯然模型欠擬合將無法做出很好的迴歸預測，所以有些方法允許在估計中引入一些偏差，從而降低預測的均方誤差。區域性線性加權的思想是對待預測點附近的每個點賦予一個權重，然後在帶權的樣本上基於最小均方誤差來進行迴歸.

普通線性迴歸：

區域性加權線性迴歸：

這裡唯一的區別是加入了權重θ,採用之前的最小二乘法求解權數w：

求偏導數：

令導數為0：

加權形式

其中加權的θ是一個矩陣，用來給每個資料點賦予權重，LWLR（Locally Weighted Linear Regression）使用‘核’來對資料點賦予權重，核的型別可以自由選擇，但一般是與距離成反比的函式，常見的是高斯核：

這樣就構造了一個只含對角元素的權重矩陣w，並且點xi與x越接近，θ(i,i)的值越大，當xi與x非常接近時，θ(i,i)的值趨於1，我們再回頭看之前的優化式：

對於一個數據點，與其靠近的點，權重大，與其相距較遠的點，權重小，從而優化問題會有所偏倚，靠近的點對該資料點的迴歸擬合起較大作用，而相距較遠的點由於權數很小，造成的影響基本可以忽略不計，這樣就等同於每個點的迴歸都是基於與其相距較近的點為基礎，而忽略了較遠的點，這也就是區域性加權線性迴歸區域性的由來，因為它著重考慮目標點區域性的資料點為迴歸基礎.

可以看到，加權函式只有一個係數，那就是分母上的K，當K取很小時，exp得到的很多值均趨於0，此時只有很少一部分樣本用於訓練，而當K取很大時，exp的值不會很快趨於0，從而會有一大部分點用於訓練，我們可以通過調整K的值，決定這個‘區域性’的大小究竟是多大.

動手看一下K對資料劃分的影響：

#畫出權數的因素k
def plot_w(k,t_p=0.5):
    x = arange(0,1,0.01)
    y = exp((x-t_p)**2/(-2*k**2))
    plt.plot(x,y)
    plt.show()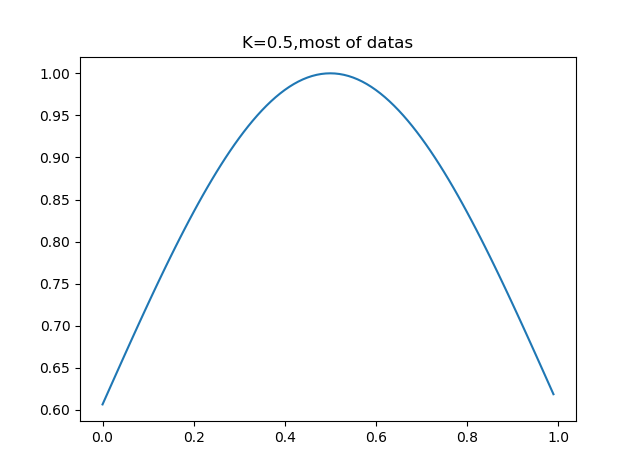

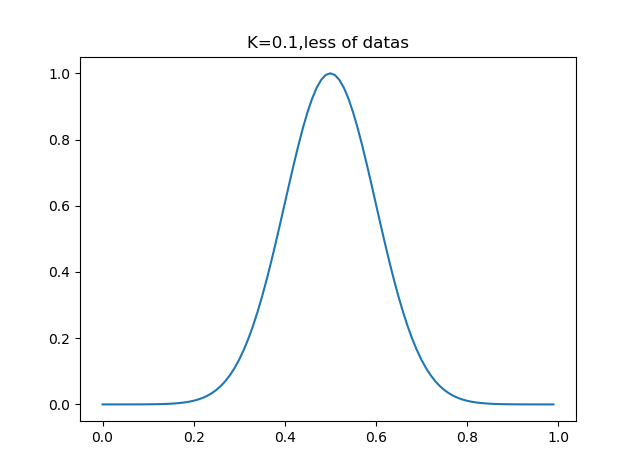
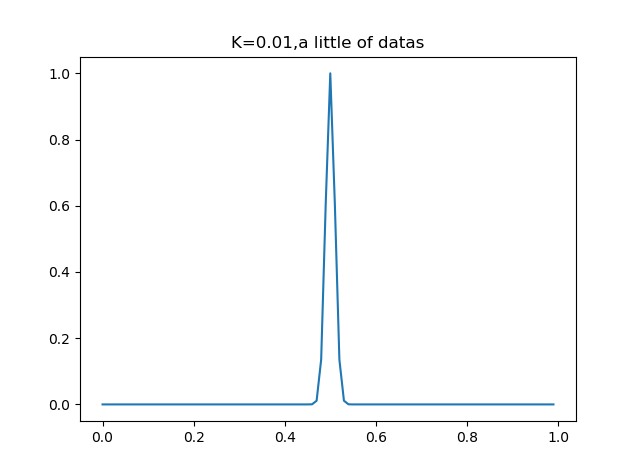
可以看到，k=0.5時，大部分資料用於迴歸模型，而當k=0.01時，只有非常靠近資料點的資料才會被迴歸模型所採用.

區域性加權迴歸實現

1）讀取資料

from numpy import *
import matplotlib.pyplot as plt

#普通線性迴歸
#讀取資料
def loadDataSet(fileName):      
    numFeat = len(open(fileName).readline().split('\t')) - 1 
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat

2）根據加權樣本計算權數W

#區域性加權線性迴歸
def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m)))#初始化一個單位矩陣
    for j in range(m):                      
        diffMat = testPoint - xMat[j,:]     
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))#計算資料點周圍資料的權數
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:#判斷是否可逆
        print ("This matrix is singular, cannot do inverse")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))#根據公式求出權數W
    return testPoint * ws

3）得到所有樣本的迴歸預測

#對所有點計算迴歸值
def lwlrTest(testArr,xArr,yArr,k=1.0): #計算所有資料點的預測迴歸值，預設k=1，即完全線性迴歸
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

4）迴歸視覺化

#畫出迴歸方程
def plot_w_figure(xArr,yArr,k=1):
    yHat = lwlrTest(xArr,xArr,yArr,k)
    xMat = mat(xArr)
    srtInd = xMat[:,1].argsort(0)#將輸入值x從大到小排序並返回索引
    xSort = xMat[srtInd][:,0,:]
    # print(xSort.shape)
    # print(xSort)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(xSort[:,1],yHat[srtInd])#繪製預測點
    ax.scatter(xMat[:,1].flatten().A[0],mat(yArr).T.flatten().A[0],s=2,c='red')#繪製初始資料點
    plt.show()

5）主函式

#主函式
if __name__ == '__main__':
    xArr,yArr=loadDataSet('ex0.txt')
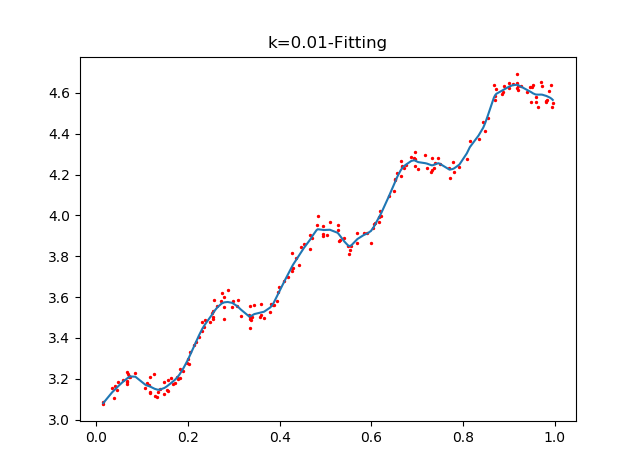
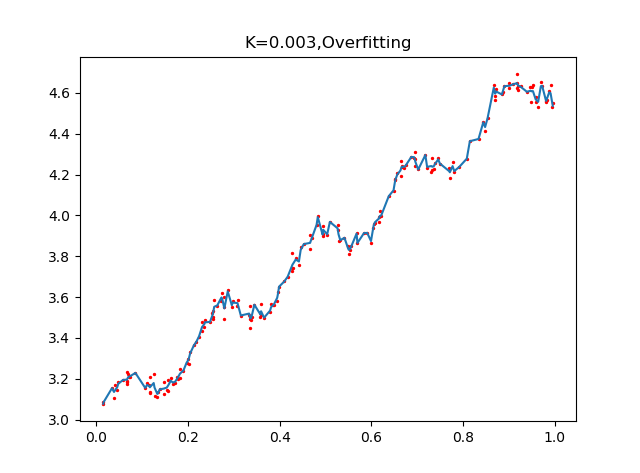
    plot_w_figure(xArr,yArr,k=0.01)

通過設定不同的k值，看看回歸的效果：

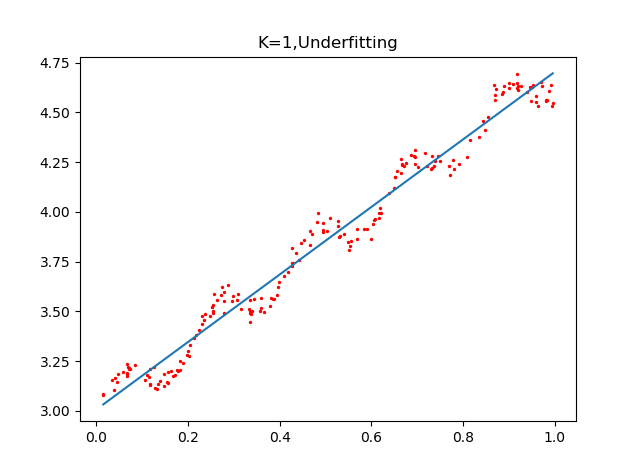
可以看到，K=1.0時，加權對樣本基本沒有影響，結果類似於之前的普通線性迴歸，k=0.01時，該模型挖掘出資料的潛在規律，而K=0.003時，引數太小導致模型考慮太多的噪聲，從而過擬合,雖然對樣本資料預測正確率很高，但對於迴歸預測而言，泛化錯誤率會非常大.

總結

可以看到，區域性加權迴歸在選擇到合適的k時，迴歸擬合的效果比普通線性迴歸好很多，但是有一點需要注意，就是區域性線性加權迴歸的計算量很大，因為對於每個資料點，都需要計算與其他資料點的距離矩陣θ，即遍歷整個資料集，因此我們還需要探索更加高效簡介的演算法，減小時間空間開銷.