機器學習(六)——區域性加權線性迴歸(Locally weighted linear regression)
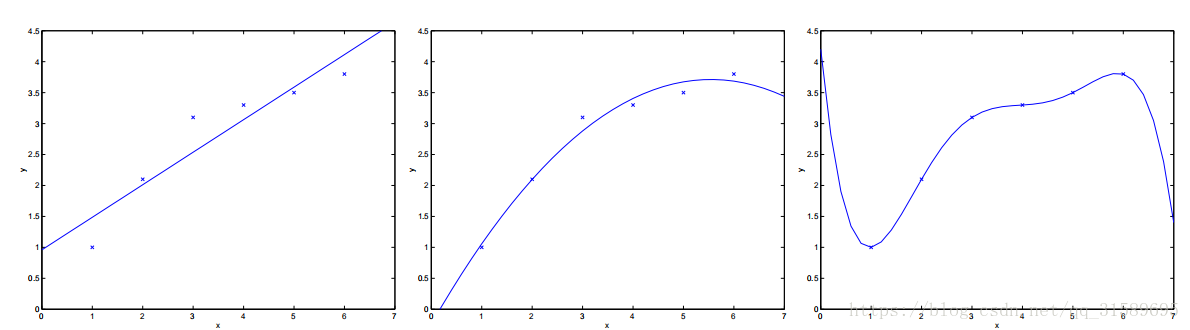
考慮從x∈R中預測y的問題。下面最左邊的圖顯示了將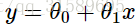
取代原來的方法,如果我們加上一個額外的特徵 x2x2,並用 y=θ0+θ1x+θ2x2y=θ0+θ1x+θ2x2 來擬合數據,你會發現效果稍微好了那麼一點(看中間這幅圖片)。似乎可以天真地認為,我們新增的特徵越多越好。然而,新增的特徵太多也是很危險的:最右邊的影象是使用一個五次多項式 y=∑5j=0θjxjy=∑j=05θjxj 來擬合數據的結果。我們看到,即使擬合曲線完美地穿過資料,我們也無法確定這就是一個相當好的預測,能夠針對不同生活地區 (x)(x) 來預測房價 (y)(y) 。在還沒有正式地定義這些術語之前,我們可以說最左側的影象展示的是一種 欠擬合(underfitting)
正如上面所看到的,特徵的選取方式能夠決定學習演算法表現效能的好壞。(當我們談到模型選擇時,我們也會見到一些演算法能夠自動選擇一些好的特徵。)在這一小節,讓我們簡要地談一談關於區域性加權線性迴歸(LWR)演算法的內容,假設我們有足夠數量的訓練集,使得對於特徵的選擇不是那麼重要。這一部分將會很短,因為你將要在你的作業中去探索關於LWR演算法的一些屬性。
在原始版本的線性迴歸演算法中,要對一個查詢點 x
- 擬合 θθ 來最小化 ∑i(y(i)−θTx(i))2∑i(y(i)−θTx(i))2
- 輸出θTxθTx
相比之下,區域性加權線性迴歸演算法做的是:
- 擬合 θθ 來最小化 ∑iw(i)(y(i)−θTx(i))2∑iw(i)(y(i)−θTx(i))2
- 輸出θTxθTx
此處的 w(i)w(i) 是非負的 權重(weights)值。直觀看來,如果對於某個特定的 ii ,它的 w(i)w(i) 很大,那麼在選擇 θθ的時候,我們將會盡可能地使 (y(i)−θTx(i))2(y(i)−θTx(i))2 更小。如果w(i)w(i) 很小,那麼在擬合的過程中 (
對於權值的選取可以使用下面這個比較標準的公式:
w(i)=exp(−(x(i)−x)22τ2)w(i)=exp(−(x(i)−x)22τ2)(如果 xx 是向量值,上面的式子需要寫成廣義形式,即 w(i)=exp(−(x(i)−x)T(x(i)−x)/2τ2)w(i)=exp(−(x(i)−x)T(x(i)−x)/2τ2),並根據情況選擇 ττ 或者 ∑∑。)
注意,權重取決於特定的點 xx, 而我們又嘗試去預測 xx。此外,如果 ∣x(i)−x∣∣x(i)−x∣ 很小,那麼 w(i)w(i) 將接近 1;如果 ∣x(i)−x∣∣x(i)−x∣ 很大,那麼 w(i)w(i) 將非常小。其直觀意義就是越是靠近預測點的樣本點,它們對預測點的影響就應該越大,越是遠離預測點的樣本點,它們對預測點的影響就越小,也就是說區域性加權線性迴歸模型只關注於預測點附近的點(這就是區域性的含義),而不考慮其他遠離預測點的樣本點。(注意,權值公式看上去類似於高斯分佈的密度,但 w(i)w(i) 和高斯分佈沒有任何關係,尤其注意 w(i)w(i) 不是隨機變數、正態分佈或者其它。)引數 ττ 控制了訓練樣本的權值根據樣本點 x(i)x(i) 到查詢點 xx 的距離下降的有多快;引數 ττ 被成為 頻寬(bandwidth) 引數。

參考最小二乘法,推導一下計算過程:
J(θ)J(θ)對 θθ 求導與上面步驟類似,得到結果為:
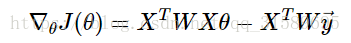
令導數為零,整理可得:
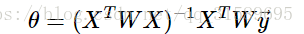
其中,WW 是 m×mm×m 維的對角矩陣,對角線依次存放 w(i)w(i) .
區域性加權線性迴歸是我們接觸的第一個 非引數(non-parametric) 演算法。之前學習的(不帶權)線性迴歸演算法是有 引數(parametric) 演算法,因為它有固定的有限數量的,能夠很好擬合數據的引數(
考慮從x∈R中預測y的問題。下面最左邊的圖顯示了將擬合到資料集的結果。我們看到資料並不是直線上的,所以擬合不是很好。取代原來的方法,如果我們加上一個額外的特徵 x2x2,並用 y=θ0+θ1x+θ2x2y=θ0+θ1x+θ2x2 來擬合數據,你會發現效果稍微好了那麼一點(看中
1. 線性迴歸
線性迴歸根據最小二乘法直接給出權值向量的解析解(closed-form solution):
w=(XTX)−1XTy
線性迴歸的一個問題就是有可能出現欠擬合現象,因為它求的是具有最小均方誤差(LSE,Least Square Erro
書籍:《機器學習實戰》中文版
IDE:PyCharm Edu 4.02
環境:Adaconda3 python3.6
注:本程式相比原書中的程式區別,主要區別在於函式驗證和繪圖部分。
一、一般線
在這篇博文中我們將會實現正則化的線性迴歸以及利用他去學習模型,不同的模型會具有不同的偏差-方差性質,我們將研究正則化以及偏差和方差之間的相互關係和影響。
這一部分的資料是關於通過一個水庫的水位來預測水庫的流水量。為了進行偏差和方差的檢驗,這裡用12組資料進行迴
在之前的部落格中我們已經簡單討論過一些迴歸的演算法,如使用假設和梯度下降法的單變數線性迴歸和多變數線性迴歸以及採用正規方程的線性迴歸,這次我們簡單討論一下區域性加權線性迴歸(Local Weighted Liner Regression)。
區域性加權迴歸可以
緊接著之前的問題,我們的目標函式定義為:
我們的目標是最小化cost function:
換成線性代數的表述方式:
是mxm維的對角矩陣
是mxn維的輸入矩陣
是mx1維的結果
是nx1維的引數向量
令
有
既
權重定義為:
引數τ控制權重函式的寬度,τ越
通常情況下的線性擬合不能很好地預測所有的值,因為它容易導致欠擬合(under fitting),比如資料集是一個鐘形的曲線。而多項式擬合能擬合所有資料,但是在預測新樣本的時候又會變得很糟糕,因為它導致資料的過擬合(overfitting),不符合資料真實的模型。 今天來講一種
區域性加權線性迴歸
線性迴歸的一個問題是有可能出現欠擬合,因為它求的是具有最小均方誤差的無偏估計,顯然模型欠擬合將無法做出很好的迴歸預測,所以有些方法允許在估計中引入一些偏差,從而降低預測的均方誤差。區域性線性加權的思想是對待預測點附近的每個點賦予一個權重,然後在帶權的樣本上基於最小均方誤差來
一、問題引入
我們現實生活中的很多資料不一定都能用線性模型描述。依然是房價問題,很明顯直線非但不能很好的擬合所有資料點,而且誤差非常大,但是一條類似二次函式的曲線卻能擬合地很好。為了解決非線性模型建立線性模型的問題,我們預測一個點的值時,選擇與這個
#!/usr/bin/python
# -*- coding:utf-8 -*-
import numpy as np
from numpy import *
import matplotlib.pyplot as plt
#處理資料函式
def loadDataSet():
Normal equation:(正規方程)
其中:X為1列值為1的vector(其對應額外的特徵變數)+xi的轉置合併的矩陣。
正規方程與梯度下降相比較的優缺點:
優點:1.不需要設定初試的學習率α
2.不需
在surpervised question中
(x,y)表示一個訓練樣本。 x為features(特徵)y為target(目標)
(xi,yi)表示訓練集。上標i just an index into the training set
Hypothesis fu
思維導圖學習筆記
自己參考BoBo老師課程講解實現:
# -*- coding: utf-8 -*-
import numpy as np
from metrics import r2_score
class LinearRegression(object):
def __
課程地址:https://coding.imooc.com/class/169.html
最小二乘法的推導部落格點選此處
程式碼實現(參考Bobo實現,如果要看BoBo老師原始碼,請點選此處):
# -*- encoding: utf-8 -*-
"""
實現簡單的線性迴歸,
自己
線性迴歸可能是統計學和機器學習中最知名且易於理解的演算法之一。
它不就是一項起源於統計學的技術嗎?
預測建模主要關注的是讓模型的誤差最小化,或者說,在可以解釋的前提下,儘可能作出最準確的預測。我們會借用,重用,甚至是竊取許多不同領域(包括統計學)的演算法,並將其用於上述的目標。
線性迴歸
【機器學習經典演算法梳理】是一個專門梳理幾大經典機器學習演算法的部落格。我在這個系列部落格中,爭取用最簡練的語言、較簡潔的數學公式,和清晰成體系的提綱,來盡我所能,對於演算法進行詳盡的梳理。【機器學習經典演算法梳理】系列部落格對於機器學習演算法的梳理,將從“基本思想”、“基本形式”、“過程推導”、“ 1、模型描述
Univariate(One variable)Linear Regression
m=訓練樣本的數目,x's=輸入的變數/特徵,y's=輸出變數/目標變數
2、代價函式
基本定義:
3、代價函式(一)
回顧一下,前面一些定義:
簡化的假設函式,theta0=0,得到假
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
path = "data"+os.sep+"creditcard.csv";
pdData = Model and Cost Function
1 模型概述 - Model Representation
To establish notation for future use, we’ll use
x(i)
the “input” variables (living area in t
注:正則化是用來防止過擬合的方法。在最開始學習機器學習的課程時,只是覺得這個方法就像某種魔法一樣非常神奇的改變了模型的引數。但是一直也無法對其基本原理有一個透徹、直觀的理解。直到最近再次接觸到這個概念,經過一番苦思冥想後終於有了我自己的理解。
0. 正則化( 相關推薦
機器學習(六)——區域性加權線性迴歸(Locally weighted linear regression)
機器學習基礎(三十) —— 線性迴歸、正則化(regularized)線性迴歸、區域性加權線性迴歸(LWLR)
機器學習實戰——線性迴歸和區域性加權線性迴歸(含python中複製的四種情形!)
機器學習5 正則化的線性迴歸(Regularized Linear Regression)和偏差對方差(Bias v.s. Variance)
區域性加權線性迴歸(內含程式碼)
區域性加權線性迴歸(Locally weighted linear regression)
區域性加權迴歸(Locally weighted linear regression)
線性模型-區域性加權線性迴歸 機器學習實戰
【機器學習】區域性加權線性迴歸
機器學習演算法與Python實踐之邏輯迴歸(Logistic Regression)(二)
Andrew機器學習課程 章節4——多變數線性迴歸
Andrew機器學習課程 章節2——單變數線性迴歸
Bobo老師機器學習筆記第五課-多元線性迴歸
Bobo老師機器學習筆記第五課-簡單線性迴歸
機器學習筆記 第5課:線性迴歸演算法
【機器學習經典演算法梳理】一.線性迴歸
吳恩達機器學習課程筆記章節二單變數線性迴歸
機器學習筆記《四》:線性迴歸,邏輯迴歸案例與重點細節問題分析
吳恩達機器學習 Coursera 筆記(二) - 單變數線性迴歸
【機器學習】正則化的線性迴歸 —— 嶺迴歸與Lasso迴歸