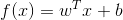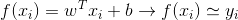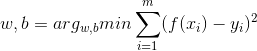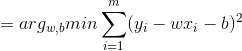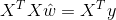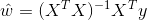線性模型-線性迴歸與實現 西瓜書
線性模型
給定d個屬性描述的例項x = (x1,x2,...,xd),其中xi是x在第i個屬性上的取值,線性模型想要學得一個通過屬性的線性組合來進行預測的函式,即:
一般寫成向量模型:
線性迴歸
給定資料集D={(x1,y1),(x2,y2),(x3,y3)...(xm,ym)} ,其中xi = (xi1,xi2,xi3,...xid) 是d維屬性向量,yi∈R,線性迴歸試圖學到一個線性模型以儘可能準確的預測實值輸出標記.即:
接下來要做的就是確定w和b,關鍵在於衡量f(x)與y的區別,這裡我們常用均方誤差作為迴歸任務中最常用的效能度量,通過最小化均方誤差得到最優的w和b.即優化:
對於這種形式,我們採用最小二乘法進行估計,為了方便計算與程式設計,這裡把w和b歸入到同一個向量w^=(w,b),相應的,資料集d表示為一個m x (d+1)大小的矩陣X,其中每行對應一個例項,由於截距項的係數固定為1不需改變,所以矩陣X最後一列均為1,前d個元素對應例項的d個屬性值,即:
再將均方誤差轉化為向量形式:
令:
對w求導,(向量可以看做是正常的二次項求導):
並令導數為0並左乘:
但這裡要注意求逆部分,只有滿秩或者正定時,上式才可以求逆,如果不滿足求逆條件,則需要引入正則化項,規範引數.
迴歸實現
1)讀取資料
#讀取資料
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t')) - 1
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat2)計算權數W
#計算w,如果不可逆則報錯
def standRegres(xArr,yArr):
xMat = mat(xArr); yMat = mat(yArr).T#轉化為向量形式
xTx = xMat.T*xMat
if linalg.det(xTx) == 0.0:#判斷是否可逆
print ("該矩陣為奇異矩陣,無法求逆!")
return
ws = xTx.I * (xMat.T*yMat)#根據公式求出w
return ws通過最小二乘法計算的結果,得到複合權數w
3)繪製迴歸直線
#畫出資料點並繪製迴歸直線
def plot_figure(xArr,yArr,ws):
xMat = mat(xArr)
yMat = mat(yArr)
yHat = xMat * ws#xi的預測值
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0],s=5)#畫出原始資料點
xcopy = xMat.copy()
xcopy.sort(0)
yHat = xcopy * ws
ax.plot(xcopy[:,1],yHat,c='r')
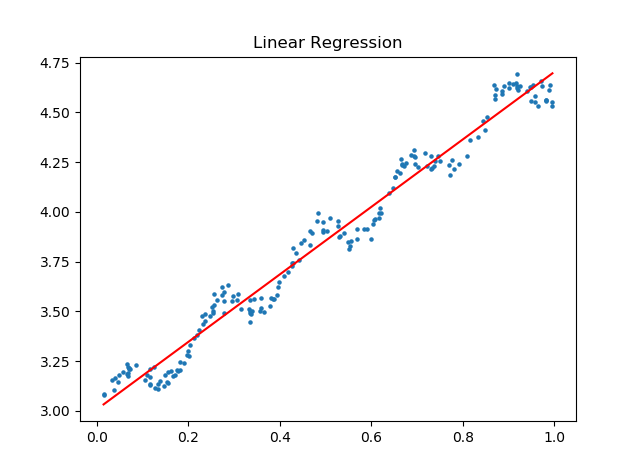
ax.set_title('Linear Regression')#畫出預測資料點
plt.show()根據線性公式和求出的引數w,分別畫出原始資料與迴歸直線進行直觀比較.
4)求相關係數
#計算迴歸後的相關係數
def print_cov(xArr,yArr,ws):
xMat = mat(xArr)
yMat = mat(yArr)
yHat = xMat * ws
cor = corrcoef(yHat.T,yMat)#自帶的求相關係數
return cor[0][1]計算迴歸前後資料的相關係數,越高說明擬合越好
5)主函式
#主函式
if __name__ == '__main__':
xArr,yArr = loadDataSet('ex0.txt')
ws = standRegres(xArr,yArr)
plot_figure(xArr,yArr,ws)
print('相關係數 : ',print_cov(xArr,yArr,ws))6)執行結果
相關係數 : 0.986473562234總結
普通線性迴歸大概就這些,主要是利用最小二乘法進行最小化均方誤差,但是在做迴歸預測時,要注意過擬合和欠擬合兩種情況的出現,過擬合主要由於模型引數過於複雜,學到了資料的噪聲,而欠擬合則因為模型過於簡單,未能很好的利用資料資訊,所以要基於二者有一個權衡,可以考慮加入正則化項,也可以考慮加入權數,下一篇介紹的區域性線性加權迴歸就是加權迴歸的例子.