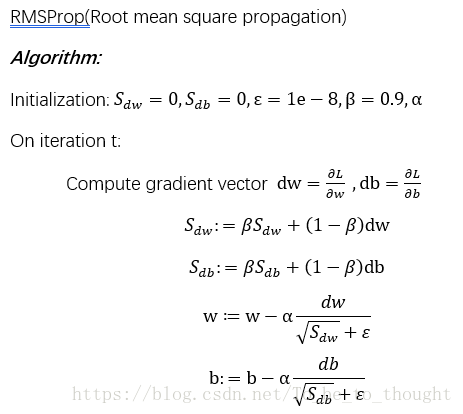https://blog.csdn.net/To_be_to_thought/article/details/81780397闡釋Batch Gradient Descent、Stochastic Gradient Descent、MiniBatch Gradient Descent具體原理。

對於梯度下降演算法，當引數特別多時容易發現，速度會變慢，需要迭代的次數更多。優化速度與學習率、梯度變化量息息相關，如何自適應地在優化過程中調整學習率和梯度變化有利於加快梯度下降的求解過程，比如在陡峭的地方變化的梯度大一點，學習率大一點等等。

下面三種演算法都是基於指數加權移動平均法考慮前面梯度對當前梯度的影響來對梯度、學習率作調整，從而更快收斂。

動量梯度下降演算法（Momentum）：                                                

前向均方根梯度下降演算法 RMSProp(Root mean square propagation)：

自適應估計演算法（Adam）

以上演算法流程均參考吳恩達老師《改善深層神經網路》視訊內容，謝謝老師的仔細講解！

下面演算法實現和測試：

import numpy as np
import math
import matplotlib.pyplot as plt

#批量梯度下降法求最小值解 所有矩陣運算一律將ndarray轉為matrix，以矩陣形式儲存的向量一律轉為列形式（n行一列的矩陣）
#alpha為學習速率，eps為一個特別小接近於0的值，迴圈種終止條件：1.達到最大迭代次數   2.損失函式變化量小於eps
#x_matrix為樣本集資料，y_list為真實值標籤
def Gradient_Descent(x_matrix,y_list,alpha,max_iter,eps):
    m,n=np.shape(x_matrix)
    #x_matrix=normalize(x_matrix)
    y_matrix=np.matrix(y_list).T
    new_X=np.matrix(np.ones((m,n+1)))
    theta=np.matrix(np.random.rand(n+1)).T#隨機生成待求引數列向量,theta行數等於new_X的列數
    for i in range(m):
        new_X[i,1:n+1]=x_matrix[i,0:n]
    last_cost=0   #上一次損失函式值，初值為0
    index=0
    loss_record=[]
    cost=cost_function(new_X,y_matrix,theta)
    while abs(last_cost-cost)>eps and index<=max_iter:
        last_cost=cost
        theta[0]=theta[0]-alpha*1/m*sum(new_X*theta-y_matrix)
        theta[1:n+1]=theta[1:n+1]-alpha*1/m*sum(new_X.T*(new_X*theta-y_matrix))
        cost=cost_function(new_X,y_matrix,theta)
        index+=1
        loss_record.append(cost)
        print(str(index)+" "+str(abs(last_cost-cost)))
    return theta,loss_record

#動量梯度下降
#alpha為學習率 beta為加權係數 max_iter為最大迭代次數 eps1為損失函式變化量閾值 eps2為梯度變化的閾值
def GD_Momentum(X,y,alpha,beta,max_iter,eps1,eps2):
    m,n_features = X.shape
    new_X = np.column_stack((X,np.ones(m)))
    theta = np.random.random(n_features+1)
    init = np.zeros(n_features+1) #指數加權移動平均法的v初值
    itera = 0
    loss_record = []
    last_cost = 0 #上一輪計算的theta對應的損失函式值
    cost = cost_function(new_X,y,theta) #當前引數向量theta下的損失函式值
    loss_record.append(cost)
    while itera < max_iter and abs(cost-last_cost) > eps1:
        last_cost = cost
        gradient = np.dot(new_X.T,(np.dot(new_X,theta)-y))
        v=beta * init[:] + (1-beta) * gradient
        theta[:] = theta[:]-alpha*1/m*v
        init[:] = v[:]
        cost = cost_function(new_X,y,theta)
        print("loss function:"+str(cost))
        itera += 1
        loss_record.append(cost)
    return theta,loss_record

#Root Mean Square Propagation的梯度下降法
#alpha為全域性學習率 beta為衰減速率 max_iter為最大迭代次數 eps1為損失函式變化量閾值 eps2為微小擾動1e-8
def GD_RMSprop(X,y,alpha,beta,max_iter,eps1,eps):
    m,n_features = X.shape     #m為樣本數，n_features為特徵數
    new_X = np.column_stack((X,np.ones(m)))
    theta = np.random.random(n_features+1)
    init_S = np.zeros(n_features+1)   #指數加權移動平均法的v初值
    itera = 0
    loss_record = []
    last_cost = 0 #上一輪計算的theta對應的損失函式值
    cost = cost_function(new_X,y,theta) #當前引數向量theta下的損失函式值
    loss_record.append(cost)
    while itera<max_iter and abs(cost-last_cost)>eps1:
        last_cost = cost
        gradient = np.dot(new_X.T,(np.dot(new_X,theta)-y))
        mean_square = beta * init_S[:] + (1-beta) * np.square(gradient)
        theta[:] = theta[:]-alpha * 1/m * gradient/(np.sqrt(mean_square)+eps)
        init_S[:] = mean_square[:]
        cost=cost_function(new_X,y,theta)
        print("loss function:"+str(cost))
        itera += 1
        loss_record.append(cost)
    return theta,loss_record

# Adaptive Moment Estimation的梯度下降法
# alpha為全域性學習率 beta1為v的衰減速率向量，一般取0.9  beta2為S的衰減速率向量，一般取0.9 max_iter為最大迭代次數 eps1為損失函式變化量閾值 eps2為微小擾動1e-8
# v和S初值為0
def GD_Adam(X,y,alpha,beta1,beta2,max_iter,eps1,eps2):
    m,n_features = X.shape               #m為樣本數，n_features為特徵數
    new_X = np.column_stack((X,np.ones(m)))
    theta = np.random.random(n_features+1)
    init_v = np.zeros(n_features+1)      #指數加權移動平均法的初值
    init_S = np.zeros(n_features+1)
    itera = 0
    loss_record = []
    last_cost = 0 #上一輪計算的theta對應的損失函式值
    cost = cost_function(new_X,y,theta) #當前引數向量theta下的損失函式值
    loss_record.append(cost)
    while itera < max_iter and abs(cost-last_cost) > eps1:
        last_cost = cost
        gradient = np.dot(new_X.T,(np.dot(new_X,theta)-y))
        v = beta1 * init_v[:] + (1-beta1) * gradient
        S = beta2 * init_S[:] + (1-beta2) * np.square(gradient)
        v_corrected = v / (1 - np.power(beta1,itera+1)) #偏差矯正
        S_corrected = S / (1 - np.power(beta2,itera+1))
        theta[:] = theta[:] - alpha * 1/m * v_corrected / (np.sqrt(S_corrected) + eps2)
        init_v[:] = v_corrected[:]
        init_S[:] = S_corrected[:]
        cost = cost_function(new_X,y,theta)
        print("loss function:"+str(cost))
        itera += 1
        loss_record.append(cost)
    return theta,loss_record

測試程式碼：

X,y_list = file2matrix('H:/Machine Learning in Action/Ch08/ex0.txt')
y = np.reshape(y_list,len(y_list))
theta4,record4=GD_Momentum(X,y,0.01,0.9,1000,1e-10,1e-9)
theta5,record5 = GD_RMSprop(X,y,0.1,0.9,100000,1e-10,1e-8)
theta6,record6 = GD_Adam(X,y,0.1,0.9,0.9,500000,1e-10,1e-8)
plt.plot(np.arange(1,len(record5)+1),record5)

引數求解結果都比較接近，損失函式衰減圖這裡就不展示了！