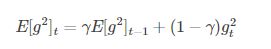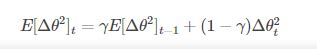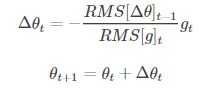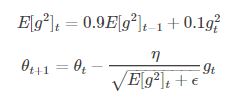梯度下降演算法是優化神經網路最常見的方式，這裡我們會接觸梯度下降法的不同變種以及多種梯度下降優化演算法。
梯度下降變種

1. batch gradient descent
   缺點：一次引數更新需要使用整個資料集，因此十分慢，並且記憶體不夠的話很難應付。
   優點：保證收斂到全域性最小值或者區域性最小值
2. stochastic gradient descent
   一次引數更新使用一個樣本
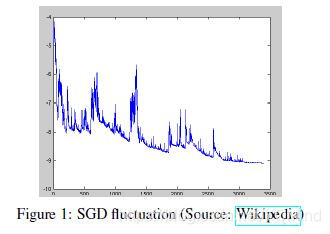
   優點：速度快。因為SGD的波動性，一方面，可以跳到更好的區域性最小點。
   缺點：引數更新方差大，從而目標函式波動嚴重，**另一方面，**很難收斂到最小值，但是我們可以逐漸減小學習率來應對。
   
3. mini-batch gradient descent
   BGD和SGD的折中結合，減少了引數更新的方差，從而可以更穩定的收斂；可以利用矩陣優化

上面提到的有很多問題需要解決：

1. 學習率的選擇比較困難。太小的學習率使得收斂很慢，太大的學習率使得難以收斂。
2. 對所有的引數更新使用同樣的學習率。
3. 鞍點。
4. 預定義好的學習率方案太死板了，不靈活。

梯度下降優化演算法
在深度學習中廣泛使用的一階方法。
Note:二階方法，例如牛頓法，在高維資料上計算量太大，實際上不可行。

1. Momentum
   動量法是一種幫助SGD在相關方向上加速並且抑制搖擺的一種方法。動量法將歷史步長的更新向量的一個分量增加到當前的更新向量中。
   $v_{}$
   t = γ v t − 1
   + η ∂ J ( θ ) ∂ θ v_t = \gamma v_{t-1} + \eta \frac{\partial J(\theta)}{\partial \theta}
   $\theta = \theta - v_t$
   對於在梯度點處具有相同的方向的維度，其動量項增大，對於在梯度點處改變方向的維度，其動量項減小。因此，我們可以得到更快的收斂速度，同時可以減少搖擺。
2. Nesterov加速梯度下降法(NAG）
   我們希望有一個智慧的球，這個球能夠知道它將要去哪裡。NAG能夠給予動量項預知能力的方法。
   通過計算關於引數未來的近似位置的梯度，而不是關於當前的引數的梯度
   $v_t = \gamma v_{t-1} + \eta \frac{\partial J(\theta-\gamma v_{t-1})}{\partial \theta}$
   $\theta = \theta - v_t$

自適應學習率演算法：Adagrad, Adadelta,RMSprop,Adam
3. Adagrad
Adagrad通過引數來調整合適的學習率 $\eta$,對稀疏引數進行大幅度更新和對頻繁引數進行小幅度更新。Adagrad為不同的引數設定不同的學習率。
因此，Adagrad非常適合處理稀疏資料。
例如，Pennington等人利用Adagrad訓練Glove詞向量，因為低頻詞比高頻詞需要更大的步長。
$\theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{\sqrt{G_{t,i}+\epsilon}} \cdot \frac{\partial J(\theta)}{\partial \theta_{t,i}}$
其中， $G_i$是到t時刻為止，關於 $\theta_i$的梯度的平方和。有趣的是，沒有平方根的操作，演算法的效果會變得很差。
優點：無需手工調整學習率，大多數情況下， $\eta = 0.01$
缺點：學習率總是在降低以至於最終變得很小，從而停止學習
4. Adadelta
它是Adagrad的一種延申方法，以解決Adagrad的學習率單調遞減的問題。而且，無需設定預設的學習率。

$RMS[g]_t = \sqrt{E[g^2]_t+\epsilon}$

$RMS[\Delta \theta]_t=\sqrt{E[\Delta \theta^2]_t+\epsilon}$

5. RMSprop
RMSprop是一個未被髮表的自適應學習率的演算法。RMSprop和Adadelta在相同的時間內被獨立的提出，都源於對Adagrad的學習率單調遞減的問題的求解。

Hinton建議將 $\gamma$設定為0.9， $\eta=0.001$
6. Adam
Adam是另一種自適應學習率的演算法。除了像Adadelta和RMSprop一樣儲存一個指數衰減的歷史平方梯度的平均值，還儲存一個歷史梯度的指數衰減平均值
在實際應用中，Adam效果很好，與其他自適應學習率演算法相比，其收斂速度更快，學習效果更有效，而且可以糾正其他優化技術中存在的問題，如：學習率消失，收斂過慢或是高方差的引數更新導致損失函式波動較大等問題。

總結：
自適應學習率演算法能很快收斂，並快速找到引數更新中正確的目標方向；SGD,NAG和動量法收斂緩慢，且很難找到正確的方向。

[1] https://blog.csdn.net/google19890102/article/details/69942970
[2] https://zhuanlan.zhihu.com/p/27449596
[3] 學習率退火
https://blog.csdn.net/lanmengyiyu/article/details/79341487?utm_source=blogxgwz4