梯度下降演算法(1) - Python實現
阿新 • • 發佈:2018-12-07
- 演算法介紹:
梯度下降演算法是一種利用一次導數資訊求取目標函式極值的方法,也是目前應用最為廣泛的區域性優化演算法之一。其具有實現簡單、容易遷移、收斂速度較快的特徵。在求解過程中,從預設的種子點開始,根據梯度資訊逐步迭代更新,使得種子點逐漸向目標函式的極小值點移動,最終到達目標函式的極小值點。
注意,沿梯度正向移動,將獲取目標函式區域性極大值(梯度上升演算法);沿梯度反向移動,將獲取目標函式區域性極小值(梯度下降演算法)。 - 迭代公式:
設向量$\vec g_k$表示目標函式在種子點$\vec x_k$處的梯度(即一次導數)。此時,根據梯度資訊的指導,可以使得種子點更加接近該向量方向的極值點(注意,目標函式真實的極值點是全方向的)。
求取極小值,沿梯度反方向移動(即梯度下降):
\begin{equation}\label{eq_1}
\vec x_{k+1} = \vec x_k - {\lambda}_k \vec s_k
\end{equation}
求取極大值,沿梯度正方向移動(即梯度上升):
\begin{equation}\label{eq_2}
\vec x_{k+1} = \vec x_k + {\lambda}_k \vec s_k
\end{equation}
其中,$\vec s_k = \frac{\vec g_k}{\left| \vec g_k \right|}$代表歸一化梯度,${\lambda}_k$代表種子點沿梯度方向移動的步長幅度引數。
很顯然,對幅度引數${\lambda}_k$的設定也屬於演算法的一部分。最常見的有兩種方法:1)線性搜尋法;2)可調步長法。
線性搜尋法中,在種子點的梯度方向上搜尋到極值點附近的步長幅度引數${\lambda}_k$,然後移動種子點至該方向的極值點處。繼續計算種子點新的梯度方向,並在該方向上移動。直到種子點到達全方向的極值點處,迭代即可終止。
可調步長法中,通常先將${\lambda}_k$設為1。然後依據上面的迭代公式(式$\ref{eq_1}$或式$\ref{eq_2}$),預先計算下一步可能的$x_{k+1}$。如果$x_{k+1}$滿足接近極值點的要求,則將種子點由$x_k$移至$x_{k+1}$,並增加${\lambda}_k$值為原先的$1.2$倍;否則,不移動種子點,並將${\lambda}_k$值減小為原先的$0.5$倍。如此反覆迭代計算,逐步移動種子點並改變${\lambda}_k$值至找到極值點為止。由於${\lambda}_k$值隨下一步的預計算情況逐步作出調整,因此筆者也將其稱為動態調整技術。
從節省計算資源的角度考慮,以下筆者將採用動態調整技術完成對梯度下降演算法的示例,僅供參考! - Python程式碼實現:

1 import matplotlib.pyplot as plt 2 import numpy 3 4 5 class GD(object): 6 7 def __init__(self, seed=None, precision=1.E-6): 8 self.seed = GD.get_seed(seed) # 梯度下降演算法的種子點 9 self.prec = precision # 梯度下降演算法的計算精度 10 11 self.path = list() # 記錄種子點的路徑及相應的目標函式值 12 self.solve() # 求解主體 13 self.display() # 資料視覺化展示 14 15 def solve(self): 16 x_curr = self.seed 17 val_curr = GD.func(*x_curr) 18 self.path.append((x_curr, val_curr)) 19 20 omega = 1 21 while omega > self.prec: 22 x_delta = omega * GD.get_grad(*x_curr) 23 x_next = x_curr - x_delta # 沿梯度反向迭代 24 val_next = GD.func(*x_next) 25 26 if numpy.abs(val_next - val_curr) < self.prec: 27 break 28 29 if val_next < val_curr: 30 x_curr = x_next 31 val_curr = val_next 32 omega *= 1.2 33 self.path.append((x_curr, val_curr)) 34 else: 35 omega *= 0.5 36 37 def display(self): 38 print('Iteration steps: {}'.format(len(self.path))) 39 print('Seed: ({})'.format(', '.join(str(item) for item in self.path[0][0]))) 40 print('Solution: ({})'.format(', '.join(str(item) for item in self.path[-1][0]))) 41 42 fig = plt.figure(figsize=(10, 4)) 43 44 ax1 = plt.subplot(1, 2, 1) 45 ax2 = plt.subplot(1, 2, 2) 46 47 ax1.plot(numpy.array(range(len(self.path))) + 1, numpy.array(list(item[1] for item in self.path)), 'k.') 48 ax1.plot(1, self.path[0][1], 'go', label='starting point') 49 ax1.plot(len(self.path), self.path[-1][1], 'r*', label='solution') 50 ax1.set(xlabel='$iterCnt$', ylabel='$iterVal$') 51 ax1.legend() 52 53 x = numpy.linspace(-100, 100, 500) 54 y = numpy.linspace(-100, 100, 500) 55 x, y = numpy.meshgrid(x, y) 56 z = GD.func(x, y) 57 ax2.contour(x, y, z, levels=36) 58 59 x2 = numpy.array(list(item[0][0] for item in self.path)) 60 y2 = numpy.array(list(item[0][1] for item in self.path)) 61 ax2.plot(x2, y2, 'k--', linewidth=2) 62 ax2.plot(x2[0], y2[0], 'go', label='starting point') 63 ax2.plot(x2[-1], y2[-1], 'r*', label='solution') 64 65 ax2.set(xlabel='$x$', ylabel='$y$') 66 ax2.legend() 67 68 fig.tight_layout() 69 fig.savefig('test_plot.png', dpi=500) 70 71 plt.show() 72 plt.close() 73 74 # 內部種子生成函式 75 @staticmethod 76 def get_seed(seed): 77 if seed is not None: 78 return numpy.array(seed) 79 return numpy.random.uniform(-100, 100, 2) 80 81 # 目標函式 82 @staticmethod 83 def func(x, y): 84 return 5 * x ** 2 + 2 * y ** 2 + 3 * x - 10 * y + 4 85 86 # 目標函式的歸一化梯度 87 @staticmethod 88 def get_grad(x, y): 89 grad_ori = numpy.array([10 * x + 3, 4 * y - 10]) 90 length = numpy.linalg.norm(grad_ori) 91 if length == 0: 92 return numpy.zeros(2) 93 return grad_ori / length 94 95 96 if __name__ == '__main__': 97 GD()
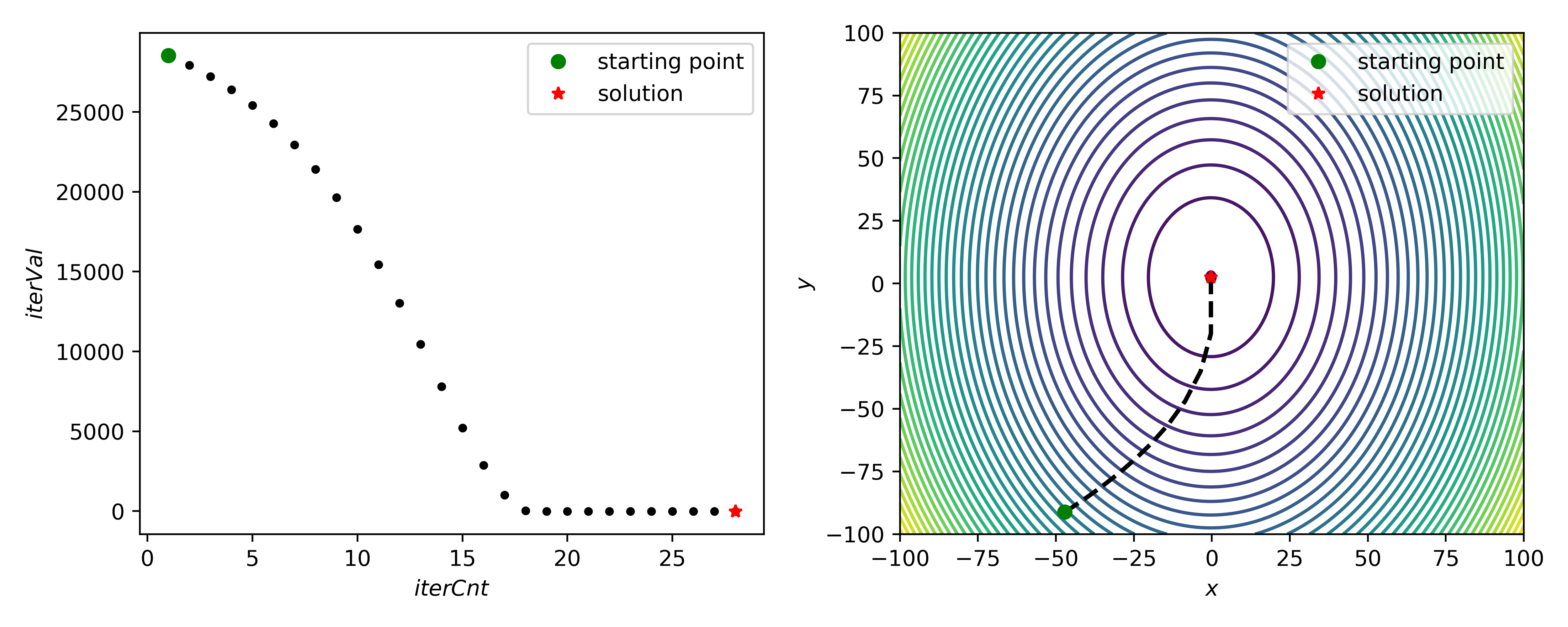
View Code筆者所用示例函式為:
\begin{equation}
f(x, y) = 5x^2 + 2y^2 + 3x - 10y + 4
\end{equation} - 結果展示: