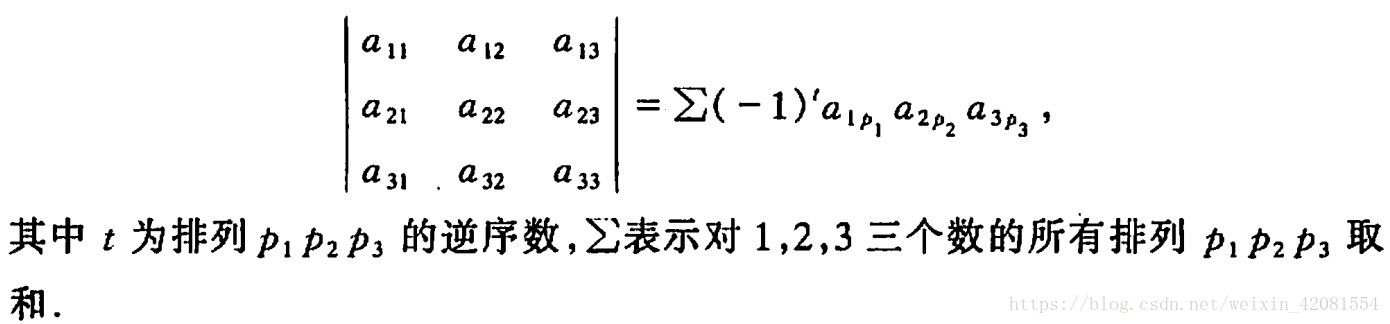一、二階和三階行列式

1.二階行列式

PS：只適用於二元線性方程；

2.三階行列式

二、全排列及其逆序數

1.全排列

把n個不同的元素排成一列，叫做這n個元素的全排列；

2.逆序數

對於n個不同的元素，先規定各元素之間有一個標準次序，於是在這n個元素的任一排列中，當某兩個元素的先後次序與標準次序不同時，就說有一個一個逆序，一個排列中所有逆序的總數叫做這個排列的逆序數。逆序數為奇數的排列叫做奇排列，為偶數的的排列叫做偶排列；

三、n階行列式的定義

由三階行列式入手，三階行列式可以寫成

以此類推，可以推廣到一般n階行列式

四、對換

在排列中，將任意兩個元素對調，其餘的元素不動，這種作出新排列的手續叫做對換，將相鄰兩個元素對換，叫做相鄰對換；

1.一個排列中的任意兩個元素對換，排列改變奇偶性；

推論：奇排列變成標準排列的對換次數為奇數，偶排列則為偶數；

2.

五、行列式的性質

1.行列式和他的轉置行列式相等；

2.互換行列式的兩行（列），行列式變號；

推論：如果行列式有兩行（列）完全相等，則此行列式等於零；

3.行列式的某一行（列）中的所有元素都乘以同一數k，等於用k乘此行列式；

推論：行列式中的某一行（列）的所有元素的公因子可以提到行列式記號的外面；

六、行列式按行（列）展開

1.

引理:一個n階行列式，如果其中第i行所有元素除（i，j）元a（ij）外都為零，那麼這行列式等於a（ij）與它的代數餘子式的乘積，即

2.行列式等於它的任一行（列）的各元素與其對應的代數餘子式乘積之和，即

這個定理叫做行列式按行（列）展開法則，利用這一法則可以簡化行列式的性質；

 七、克拉默法則

1.

2.如果線性方程組的係數行列式D不等於0，則其一定有解，且解是唯一的；反之，如果方程組無解或有兩個不同的解，則它的係數行列式必為零；

3.對於齊次線性方程（即等式右邊全為0），如果係數行列式D不等於0，則齊次線性方程組沒有非零解；反之，如果有非零解，則係數行列式必為0；