1.條件概率      

設A,B是兩個事件，且P(B)>0,則在事件B發生的條件下，事件A發生的條件概率（conditional probability)為：

                     P(A|B)=P(AB)/P(B)

分析：一般說到條件概率這一概念的時候，事件A和事件B都是同一實驗下的不同的結果集合，事件A和事件B一般是有交集的，若沒有交集（互斥），則條件概率為0，例如：

① 扔骰子，扔出的點數介於[1,3]稱為事件A，扔出的點數介於[2,5]稱為事件B，問：B已經發生的條件下，A發生的概率是多少？

也即，做一次實驗時，即有可能僅發生A，也有可能僅發生B，也有可能AB同時發生，

② 同時扔3個骰子，“三個數都不一樣”稱為事件A，“其中有一個點數為1”稱為事件B。這一題目中，AB也是有交集的。

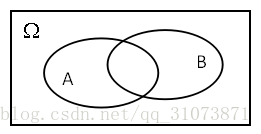
用圖更能容易的說明上述問題，我們進行某一實驗，某一實驗所有的可能的樣本的結合為Ω（也即窮舉實驗的所有樣本），圓圈A代表事件A所能囊括的所有樣本，圓圈B代表事件B所能囊括的所有樣本。

由圖再來理解一下這個問題：“B已經發生的條件下，A發生的概率”，

這句話中，“B已經發生”就相當於已經把樣本的可選範圍限制在了圓圈B中，

其實就等價於這句話：“在圓圈B中，A發生的概率”，顯然P(A|B)就等於AB交集中樣本的數目/B的樣本數目。

為什麼這裡用的是樣本的數目相除，而上面的公式卻是用的概率相除，原因很簡單，用樣本數目相除時，把分子分母同除以總樣本數，這就變成了概率相除。

2.聯合概率

聯合概率指的是包含多個條件且所有條件同時成立的概率，記作P(X=a,Y=b)或P(a,b)，有的書上也習慣記作P(ab)，但是這種記法個人不太習慣，所以下文采用以逗號分隔的記法。

一定要注意是所有條件同時成立！

3.邊緣概率

邊緣概率是與聯合概率對應的，P(X=a)或P(Y=b)，這類僅與單個隨機變數有關的概率稱為邊緣概率

參考：

https://blog.csdn.net/tick_tock97/article/details/79885868#commentBox

https://blog.csdn.net/qq_31073871/article/details/81077386