梯度上升演算法與隨機梯度上升演算法的實現
1. 引言
上一篇日誌中,我們最終推匯出了計算最優係數的公式。
Logistic 迴歸數學公式推導
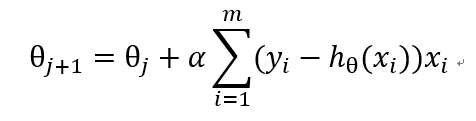
本文,我們就利用上一篇文章中計算出的公式來實現模型的訓練和資料的分類。
2. 通過 python 實現 logistic 演算法
有了上一篇日誌中的公式,《機器學習實戰》中的程式碼就非常容易理解了:
# -*- coding:UTF-8 -*-
# {{{
import matplotlib.pyplot as plt
import numpy as np
def loadDataSet():
"""
生成資料矩陣與標籤矩陣
:return: 資料矩陣與標籤矩陣
""" 
訓練樣本資料見本文的附錄。
3. 隨機梯度上升演算法
當資料量達到上億或更多資料以後,梯度上升演算法中的矩陣乘法等操作顯然耗時將上升到非常高的程度,那麼,我們是否可以不用整個資料集作為樣本來計算其權重引數而是隻使用其中的一部分資料來訓練呢?
這個演算法思想就是隨機梯度上升演算法,他通過隨機取資料集中的部分資料,來代表整體資料集,從而實現對資料樣本集的縮小,達到減少計算量,降低演算法時間複雜度的目的。
3.1. 演算法程式碼
def randGradientAscent(dataMatrix, classLabels, numIter=20):
"""
隨機梯度上升演算法
:param dataMatrix: 資料矩陣
:param classLabels: 標籤矩陣
:param numIter: 外迴圈次數
:return: 權重陣列與迴歸係數矩陣
"""
time0 = time.time()
m,n = np.shape(dataMatrix)
weights = np.ones(n)
weights_array = np.array([])
innerIterNum = int(m/100)
for j in range(numIter):
dataIndex = list(range(m))
for i in range(innerIterNum):
alpha = 4/(1.0 + j + i) + 0.01 # 降低alpha的大小,每次減小1/(j+i)
""" 隨機選取樣本 """
randIndex = int(random.uniform(0,len(dataIndex)))
chose = dataIndex[randIndex]
h = sigmoid(sum(dataMatrix[chose]*weights))
error = classLabels[chose] - h
weights = weights + alpha * error * dataMatrix[chose]
weights_array = np.append(weights_array,weights,axis=0)
del(dataIndex[randIndex])
weights_array = weights_array.reshape(numIter*innerIterNum, n)
print("隨機梯度演算法耗時:", time.time() - time0)
return weights, weights_array
上述程式碼與梯度上升演算法相比,主要有以下改進:
- 將原有的迭代 + 矩陣操作替換成內外層雙層迴圈實現,內迴圈只隨機選取原資料集的 1/100 規模,從而實現計算量的縮減
- alpha 動態調整,隨著內迴圈的進行,逐步縮小,從而對獲取更準確的最優值與執行時間二者的優化
4. 隨機梯度上升演算法與梯度上升演算法效果對比
下面程式碼對比了梯度上升演算法與隨機梯度上升演算法的效果。
# -*- coding:UTF-8 -*-
# {{{
import time
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
import random
def loadDataSet():
"""
載入資料
:return: 資料集,標籤集
"""
dataMat = []
labelMat = []
fr = open('test_dataset.txt')
for line in fr.readlines():
for i in range(100):
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
fr.close()
return dataMat, labelMat
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
def gradAscent(dataMatIn, classLabels, maxCycles = 300):
"""
梯度上升演算法
:param dataMatIn: 資料矩陣
:param classLabels: 資料集
:param maxCycles: 迭代次數
:return: 權重陣列與迴歸係數矩陣
"""
time0 = time.time()
dataMatrix = np.mat(dataMatIn)
labelMat = np.mat(classLabels).transpose()
m, n = np.shape(dataMatrix)
alpha = 0.0001
weights = np.ones((n,1))
weights_array = np.array([])
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights)
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
weights_array = np.append(weights_array,weights)
weights_array = weights_array.reshape(maxCycles,n)
print("梯度上升演算法耗時:", time.time() - time0)
return weights.getA(), weights_array
def randGradientAscent(dataMatrix, classLabels, numIter=20):
"""
隨機梯度上升演算法
:param dataMatrix: 資料矩陣
:param classLabels: 標籤矩陣
:param numIter: 外迴圈次數
:return: 權重陣列與迴歸係數矩陣
"""
time0 = time.time()
m,n = np.shape(dataMatrix)
weights = np.ones(n)
weights_array = np.array([])
innerIterNum = int(m/100)
for j in range(numIter):
dataIndex = list(range(m))
for i in range(innerIterNum):
alpha = 4/(1.0 + j + i) + 0.01 #降低alpha的大小,每次減小1/(j+i)
""" 隨機選取樣本 """
randIndex = int(random.uniform(0,len(dataIndex)))
chose = dataIndex[randIndex]
h = sigmoid(sum(dataMatrix[chose]*weights))
error = classLabels[chose] - h
weights = weights + alpha * error * dataMatrix[chose]
weights_array = np.append(weights_array,weights,axis=0)
del(dataIndex[randIndex])
weights_array = weights_array.reshape(numIter*innerIterNum, n)
print("隨機梯度演算法耗時:", time.time() - time0)
return weights, weights_array
def plotWeights(rand_gradientascent_weights, gradient_ascent_weights):
"""
繪製迴歸係數與迭代次數的關係
:param rand_gradientascent_weights: 隨機梯度上升權重矩陣
:param gradient_ascent_weights: 梯度上升權重矩陣
:return:
"""
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
"""
將fig畫布分隔成1行1列,不共享x軸和y軸,fig畫布的大小為 (13,8),分為六個區域
"""
fig, axs = plt.subplots(nrows=3, ncols=2, sharex='none', sharey='none', figsize=(20,10))
x1 = np.arange(0, len(rand_gradientascent_weights), 1)
axs[0][0].plot(x1, rand_gradientascent_weights[:, 0])
axs0_title_text = axs[0][0].set_title(u'改進的隨機梯度上升演算法:迴歸係數與迭代次數關係',FontProperties=font)
axs0_ylabel_text = axs[0][0].set_ylabel(u'W0',FontProperties=font)
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
axs[1][0].plot(x1, rand_gradientascent_weights[:, 1])
axs1_ylabel_text = axs[1][0].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
axs[2][0].plot(x1, rand_gradientascent_weights[:, 2])
axs2_xlabel_text = axs[2][0].set_xlabel(u'迭代次數',FontProperties=font)
axs2_ylabel_text = axs[2][0].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
x2 = np.arange(0, len(gradient_ascent_weights), 1)
axs[0][1].plot(x2, gradient_ascent_weights[:, 0])
axs0_title_text = axs[0][1].set_title(u'梯度上升演算法:迴歸係數與迭代次數關係',FontProperties=font)
axs0_ylabel_text = axs[0][1].set_ylabel(u'W0',FontProperties=font)
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
axs[1][1].plot(x2, gradient_ascent_weights[:, 1])
axs1_ylabel_text = axs[1][1].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
axs[2][1].plot(x2, gradient_ascent_weights[:, 2])
axs2_xlabel_text = axs[2][1].set_xlabel(u'迭代次數',FontProperties=font)
axs2_ylabel_text = axs[2][1].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
weights1,weights_array1 = randGradientAscent(np.array(dataMat), labelMat)
weights2,weights_array2 = gradAscent(dataMat, labelMat)
plotWeights(weights_array1, weights_array2)
# }}}
首先將資料集通過複製 100 次,從而實現將原有訓練資料集從 100 個變為 10000 個的效果。
然後,我們畫出了迭代過程中的權重變化曲線。
4.1. 輸出結果
輸出了:
隨機梯度演算法耗時: 0.03397965431213379
梯度上升演算法耗時: 0.11360883712768555

4.2. 結果分析
可以看到,兩個演算法都剛好在我們迭代結束時趨於平衡,這是博主為了對比兩個演算法執行的時間對迭代次數進行多次調整的結果。
結果已經非常明顯,雖然從波動範圍來看,隨機梯度上升演算法在迭代過程中更加不穩定,但隨機梯度上升演算法的收斂時間僅僅是梯度上升演算法的30%,時間大為縮短,如果資料規模進一步上升,則差距將會更加明顯。
而從結果看,兩個演算法的最終收斂位置是非常接近的,但是,從原理上來說,隨機梯度演算法效果確實可能遜於梯度上升演算法,但這仍然取決於步進係數、內外層迴圈次數以及隨機樣本選取數量的選擇。
5. 《機器學習實戰》隨機梯度上升演算法講解中的錯誤
幾天前,閱讀《機器學習實戰》時,對於作者所寫的程式碼例子,有很多疑問,經過幾天的研究,確認是某種原因導致的謬誤,最終有了上文中博主自己改進過的程式碼,實現了文中的演算法思想。
這裡詳細來說一下書中原始碼和結論中存在的紕漏。
下面程式碼是書中的原始碼:
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix)
weights = ones(n) #initialize to all ones
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
randIndex = int(random.uniform(0, len(dataIndex)))#go to 0 because of the constant
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights
這段程式碼存在下面的幾個問題,盡信書不如無書,網上很多筆記和部落格都是照搬書上的程式碼和結論,而沒有進行自己的思考,這樣是不可取的。
5.1. 隨機樣本選擇時下標問題
程式碼中,randIndex 是從 0 到 dataIndex 長度 - 1的隨機數,假設訓練資料規模為 100。
那麼首次迭代中,dataIndex 是從 0 到 99 的隨機數,假設 dataIndex 取到的是 0,那麼本次迭代的訓練資料是第 0 條資料,然後,首次迭代的最後,刪除了 dataIndex 的第 0 個元素。
第二次迭代中,dataIndex 是從 0 到 98 的隨機數,假設 dataIndex 取到的是 0,那麼本次迭代的訓練資料是第 0 條資料,然後,第二次迭代的最後,刪除了 dataIndex 的第 0 個元素。
。。。
如果剛好我們的 dataIndex 每次都取到 0,那麼最終的訓練結果將毫無意義。
首先,即使這段程式碼是正確的,del(dataIndex[randIndex]) 的意義是什麼呢?dataIndex 列表存在的價值又是什麼呢?為什麼不直接用一個數字代表規模來進行每次內迭代中的自減操作呢?
所以程式碼原意是:
randIndex = dataIndex[int(random.uniform(0
