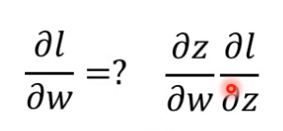反向傳播(back propagation)演算法詳解

反向傳播演算法是神經網路的基礎之一，該演算法主要用於根據損失函式來對網路引數進行優化，下面主要根據李巨集毅機器學習課程來整理反向傳播演算法，原版視訊在https://www.bilibili.com/video/av10590361/?p=14.

首先，我們來看一看優化方程：

上面的損失函式是普通的交叉熵損失函式，然後加上了正則化項，為了更新引數W，我們需要知道J關於W的偏導。

上圖是一個簡單的例子，我們擷取神經網路的一部分，根據鏈式法則(chain rule),要想知道J關於w的偏導，我們需要求出：

上面的式子也可以寫成下式，a代表activation function也就是啟用函式：

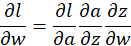
1:前向傳播（forward pass）

在前向傳播中，我們可以得到每個神經元的輸出z，以及z關於該層引數w的偏微分：

根據z的式子我們可以知道，z關於w的偏導等於該層的輸入，下圖是一個例子:

2:反向傳播(backward pass)

通過正向傳播，我們已經知道了但是還沒有求出來，而這兩項都是在反向傳播過程中得到的。

其中比較好求，因為它的值就是啟用函式的偏導，比如sigmoid函式的偏導等於z(1-z).因此現在我們只需要求解：

根據鏈式法則，等於所有分支關於a的偏導，如上圖所示。

因此求解的過程大致如下：

為了求，我們需要求解，如果直接連線輸出的話，可以按照下面求解：

如果不是直接輸出，那麼就遞迴的求解。

下面就是總的過程：

可以看出，在求解偏導的時候，需要乘以每一層的輸出z，以及啟用函式的導數，以及中間的引數w，因此在訓練神經網路的時候需要做batch normalization，使得每一層的輸入大致在一個scale下面，另外還需要加正則項防止w過大（會造成梯度爆炸），除此之外還需要設計一些好的啟用函式來防止梯度消失問題(如sigmoid的偏導最大值為0.25，因此層數加深之後會造成梯度消失）。