deeplearning.ai課程作業：Convolutional Neural Networks- Course 4 Week4

Part 1

Face Recognition for the Happy House

Welcome to the first assignment of week 4! Here you will build a face recognition system. Many of the ideas presented here are from FaceNet. In lecture, we also talked about DeepFace

.

Face recognition problems commonly fall into two categories:

• Face Verification - “is this the claimed person?”. For example, at some airports, you can pass through customs by letting a system scan your passport and then verifying that you (the person carrying the passport) are the correct person. A mobile phone that unlocks using your face is also using face verification. This is a 1:1 matching problem.
• Face Recognition - “who is this person?”. For example, the video lecture showed a face recognition video (https://www.youtube.com/watch?v=wr4rx0Spihs) of Baidu employees entering the office without needing to otherwise identify themselves. This is a 1:K matching problem.

FaceNet learns a neural network that encodes a face image into a vector of 128 numbers. By comparing two such vectors, you can then determine if two pictures are of the same person.

In this assignment, you will:

• Implement the triplet loss function
• Use a pretrained model to map face images into 128-dimensional encodings
• Use these encodings to perform face verification and face recognition

In this exercise, we will be using a pre-trained model which represents ConvNet activations using a “channels first” convention, as opposed to the “channels last” convention used in lecture and previous programming assignments. In other words, a batch of images will be of shape $(m, n_C, n_H, n_W)$ instead of $(m, n_H, n_W, n_C)$. Both of these conventions have a reasonable amount of traction among open-source implementations; there isn’t a uniform standard yet within the deep learning community.

Let’s load the required packages.

from keras.models import Sequential
from keras.layers import Conv2D, ZeroPadding2D, Activation, Input, concatenate
from keras.models import Model
from keras.layers.normalization import BatchNormalization
from keras.layers.pooling import MaxPooling2D, AveragePooling2D
from keras.layers.merge import Concatenate
from keras.layers.core import Lambda, Flatten, Dense
from keras.initializers import glorot_uniform
from keras.engine.topology import Layer
from keras import backend as K
K.set_image_data_format('channels_first')
import cv2
import os
import numpy as np
from numpy import genfromtxt
import pandas as pd
import tensorflow as tf
from fr_utils import *
from inception_blocks_v2 import *

%matplotlib inline
%load_ext autoreload
%autoreload 2

np.set_printoptions(threshold=np.nan)

0 - Naive Face Verification

In Face Verification, you’re given two images and you have to tell if they are of the same person. The simplest way to do this is to compare the two images pixel-by-pixel. If the distance between the raw images are less than a chosen threshold, it may be the same person!

Figure 1

Of course, this algorithm performs really poorly, since the pixel values change dramatically due to variations in lighting, orientation of the person’s face, even minor changes in head position, and so on.

You’ll see that rather than using the raw image, you can learn an encoding $f(img)$ so that element-wise comparisons of this encoding gives more accurate judgements as to whether two pictures are of the same person.

1 - Encoding face images into a 128-dimensional vector

1.1 - Using an ConvNet to compute encodings

The FaceNet model takes a lot of data and a long time to train. So following common practice in applied deep learning settings, let’s just load weights that someone else has already trained. The network architecture follows the Inception model from Szegedy et al.. We have provided an inception network implementation. You can look in the file inception_blocks.py to see how it is implemented (do so by going to “File->Open…” at the top of the Jupyter notebook).

The key things you need to know are:

• This network uses 96x96 dimensional RGB images as its input. Specifically, inputs a face image (or batch of $m$ face images) as a tensor of shape $(m, n_C, n_H, n_W) = (m, 3, 96, 96)$
• It outputs a matrix of shape $(m, 128)$ that encodes each input face image into a 128-dimensional vector

Run the cell below to create the model for face images.

FRmodel = faceRecoModel(input_shape=(3, 96, 96))

print("Total Params:", FRmodel.count_params())

Total Params: 3743280

Expected Output

Total Params: 3743280

By using a 128-neuron fully connected layer as its last layer, the model ensures that the output is an encoding vector of size 128. You then use the encodings the compare two face images as follows:

Figure 2:
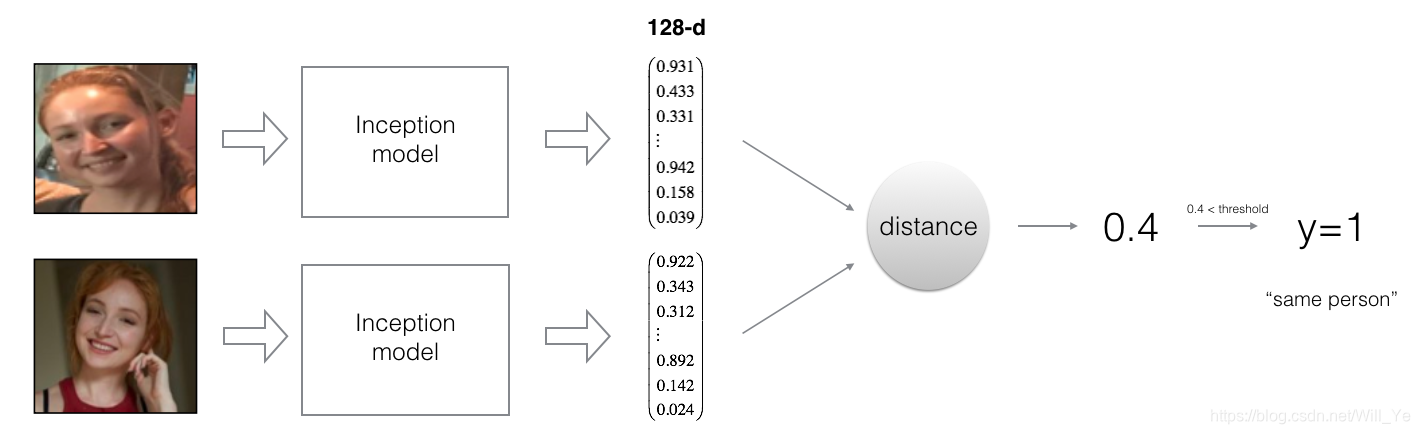
By computing a distance between two encodings and thresholding, you can determine if the two pictures represent the same person

So, an encoding is a good one if:

• The encodings of two images of the same person are quite similar to each other
• The encodings of two images of different persons are very different

The triplet loss function formalizes this, and tries to “push” the encodings of two images of the same person (Anchor and Positive) closer together, while “pulling” the encodings of two images of different persons (Anchor, Negative) further apart.

Figure 3:
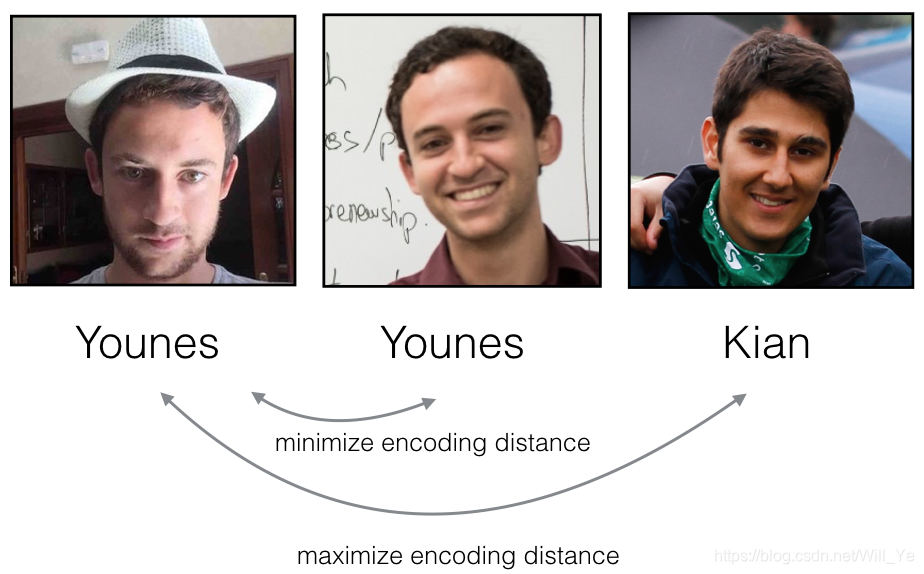
In the next part, we will call the pictures from left to right: Anchor (A), Positive §, Negative (N)

1.2 - The Triplet Loss

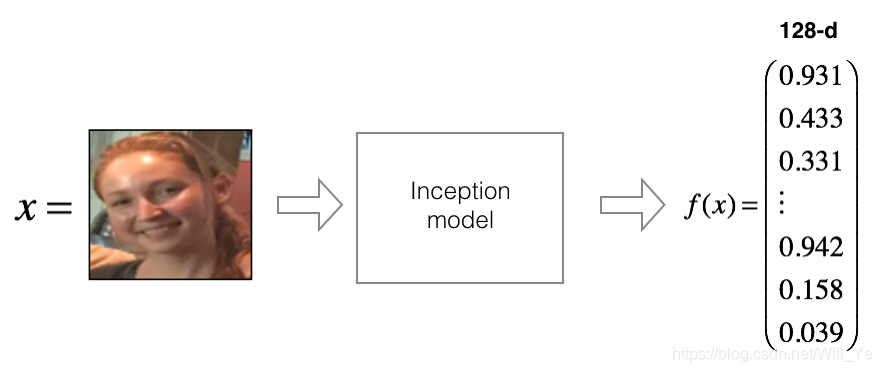
For an image $x$, we denote its encoding $f(x)$, where $f$ is the function computed by the neural network.

Training will use triplets of images $(A, P, N)$:

• A is an “Anchor” image–a picture of a person.
• P is a “Positive” image–a picture of the same person as the Anchor image.
• N is a “Negative” image–a picture of a different person than the Anchor image.

These triplets are picked from our training dataset. We will write $(A^{(i)}, P^{(i)}, N^{(i)})$ to denote the $i$-th training example.

You’d like to make sure that an image $A^{(i)}$ of an individual is closer to the Positive $P^{(i)}$ than to the Negative image $N^{(i)}$) by at least a margin $\alpha$:

$\mid \mid f(A^{(i)}) - f(P^{(i)}) \mid \mid_2^2 + \alpha < \mid \mid f(A^{(i)}) - f(N^{(i)}) \mid \mid_2^2$

You would thus like to minimize the following “triplet cost”:

$\mathcal{J} = \sum^{m}_{i=1} \large[ \small \underbrace{\mid \mid f(A^{(i)}) - f(P^{(i)}) \mid \mid_2^2}_\text{(1)} - \underbrace{\mid \mid f(A^{(i)}) - f(N^{(i)}) \mid \mid_2^2}_\text{(2)} + \alpha \large ] \small_+ \tag{3}$

Here, we are using the notation “ $[z]_+$” to denote $max(z,0)$.

Notes:

• The term (1) is the squared distance between the anchor “A” and the positive “P” for a given triplet; you want this to be small.
• The term (2) is the squared distance between the anchor “A” and the negative “N” for a given triplet, you want this to be relatively large, so it thus makes sense to have a minus sign preceding it.
• $\alpha$ is called the margin. It is a hyperparameter that you should pick manually. We will use $\alpha = 0.2$.

Most implementations also normalize the encoding vectors to have norm equal one (i.e., $\mid \mid f(img)\mid \mid_2$=1); you won’t have to worry about that here.

Exercise: Implement the triplet loss as defined by formula (3). Here are the 4 steps:

1. Compute the distance between the encodings of “anchor” and “positive”: $\mid \mid f(A^{(i)}) - f(P^{(i)}) \mid \mid_2^2$