deeplearning.ai課程作業：Convolutional Neural Networks- Course 4 Week 1

Part 1

Convolutional Neural Networks: Step by Step

Welcome to Course 4’s first assignment! In this assignment, you will implement convolutional (CONV) and pooling (POOL) layers in numpy, including both forward propagation and (optionally) backward propagation.

Notation:

• Superscript $[l]$ denotes an object of the $l^{}$

  t h l^{th} layer.
  • Example: $a^{[}$
    4 ] a^{[4]} is the $4^{th}$ layer activation. $W^{[5]}$ and $b^{[5]}$ are the $5^{th}$ layer parameters.

• Superscript $(i)$ denotes an object from the $i^{th}$ example.

  • Example: $x^{(i)}$ is the $i^{th}$ training example input.

• Lowerscript $i$ denotes the $i^{th}$ entry of a vector.

  • Example: $a^{[l]}_i$ denotes the $i^{th}$ entry of the activations in layer $l$, assuming this is a fully connected (FC) layer.

• $n_H$, $n_W$ and $n_C$ denote respectively the height, width and number of channels of a given layer. If you want to reference a specific layer $l$, you can also write $n_H^{[l]}$, $n_W^{[l]}$, $n_C^{[l]}$.

• $n_{H_{prev}}$, $n_{W_{prev}}$ and $n_{C_{prev}}$ denote respectively the height, width and number of channels of the previous layer. If referencing a specific layer $l$, this could also be denoted $n_H^{[l-1]}$, $n_W^{[l-1]}$, $n_C^{[l-1]}$.

We assume that you are already familiar with numpy and/or have completed the previous courses of the specialization. Let’s get started!

1 - Packages

Let’s first import all the packages that you will need during this assignment.

• numpy is the fundamental package for scientific computing with Python.
• matplotlib is a library to plot graphs in Python.
• np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work.

import numpy as np
import h5py
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)

2 - Outline of the Assignment

You will be implementing the building blocks of a convolutional neural network! Each function you will implement will have detailed instructions that will walk you through the steps needed:

• Convolution functions, including:
  • Zero Padding
  • Convolve window
  • Convolution forward
  • Convolution backward (optional)
• Pooling functions, including:
  • Pooling forward
  • Create mask
  • Distribute value
  • Pooling backward (optional)

This notebook will ask you to implement these functions from scratch in numpy. In the next notebook, you will use the TensorFlow equivalents of these functions to build the following model:
Note that for every forward function, there is its corresponding backward equivalent. Hence, at every step of your forward module you will store some parameters in a cache. These parameters are used to compute gradients during backpropagation.

3 - Convolutional Neural Networks

Although programming frameworks make convolutions easy to use, they remain one of the hardest concepts to understand in Deep Learning. A convolution layer transforms an input volume into an output volume of different size, as shown below.

In this part, you will build every step of the convolution layer. You will first implement two helper functions: one for zero padding and the other for computing the convolution function itself.

3.1 - Zero-Padding

Zero-padding adds zeros around the border of an image:
The main benefits of padding are the following:

• It allows you to use a CONV layer without necessarily shrinking the height and width of the volumes. This is important for building deeper networks, since otherwise the height/width would shrink as you go to deeper layers. An important special case is the “same” convolution, in which the height/width is exactly preserved after one layer.

• It helps us keep more of the information at the border of an image. Without padding, very few values at the next layer would be affected by pixels as the edges of an image.

Exercise: Implement the following function, which pads all the images of a batch of examples X with zeros. Use np.pad. Note if you want to pad the array “a” of shape $(5,5,5,5,5)$ with pad = 1 for the 2nd dimension, pad = 3 for the 4th dimension and pad = 0 for the rest, you would do:

a = np.pad(a, ((0,0), (1,1), (0,0), (3,3), (0,0)), 'constant', constant_values = (..,..))

# GRADED FUNCTION: zero_pad

def zero_pad(X, pad):
    """
    Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image, 
    as illustrated in Figure 1.
    
    Argument:
    X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images
    pad -- integer, amount of padding around each image on vertical and horizontal dimensions
    
    Returns:
    X_pad -- padded image of shape (m, n_H + 2*pad, n_W + 2*pad, n_C)
    """
    
    ### START CODE HERE ### (≈ 1 line)
    X_pad = np.pad(X, ((0,0), (2,2), (2,2), (0,0)), 'constant', constant_values = (0,0))
    # constant——values這個引數值的意思是，我們要填充的數值，一般都設為0
    ### END CODE HERE ###
    
    return X_pad

np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
x_pad = zero_pad(x, 2)
print ("x.shape =", x.shape)
print ("x_pad.shape =", x_pad.shape)
print ("x[1,1] =", x[1,1])
print ("x_pad[1,1] =", x_pad[1,1])

fig, axarr = plt.subplots(1, 2)
axarr[0].set_title('x')
axarr[0].imshow(x[0,:,:,0])
axarr[1].set_title('x_pad')
axarr[1].imshow(x_pad[0,:,:,0])

x.shape = (4, 3, 3, 2)
x_pad.shape = (4, 7, 7, 2)
x[1,1] = [[ 0.90085595 -0.68372786]
 [-0.12289023 -0.93576943]
 [-0.26788808  0.53035547]]
x_pad[1,1] = [[ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]
 [ 0.  0.]]

Expected Output:

x.shape:	(4, 3, 3, 2)
x_pad.shape:	(4, 7, 7, 2)
x[1,1]:	[[ 0.90085595 -0.68372786] [-0.12289023 -0.93576943] [-0.26788808 0.53035547]]
x_pad[1,1]:	[[ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.]]

3.2 - Single step of convolution

In this part, implement a single step of convolution, in which you apply the filter to a single position of the input. This will be used to build a convolutional unit, which:

• Takes an input volume
• Applies a filter at every position of the input
• Outputs another volume (usually of different size)

Figure 2 : Convolution operation
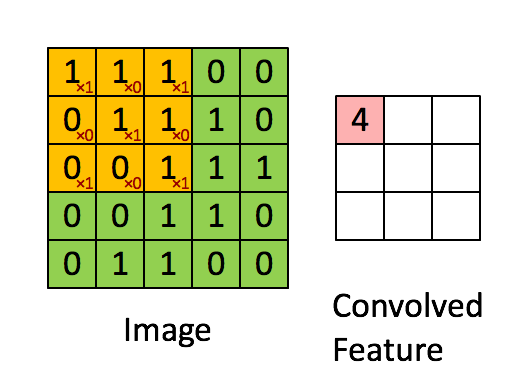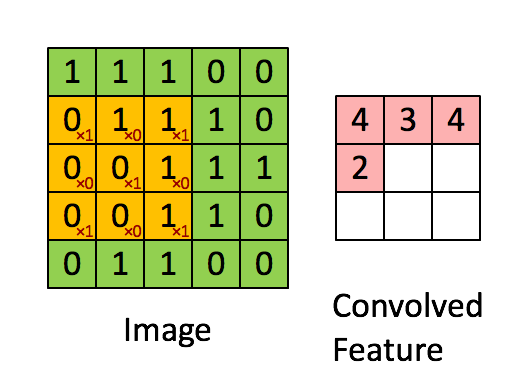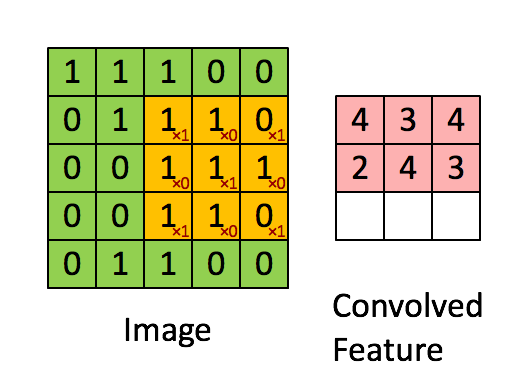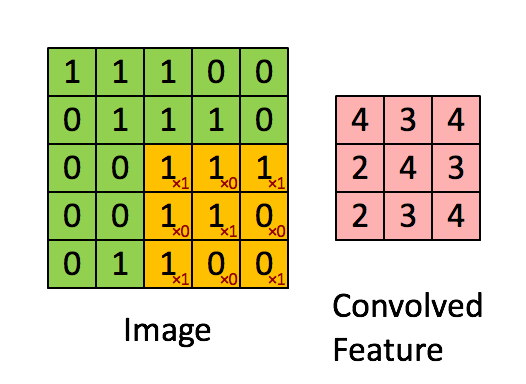
with a filter of 2x2 and a stride of 1 (stride = amount you move the window each time you slide)

In a computer vision application, each value in the matrix on the left corresponds to a single pixel value, and we convolve a 3x3 filter with the image by multiplying its values element-wise with the original matrix, then summing them up and adding a bias. In this first step of the exercise, you will implement a single step of convolution, corresponding to applying a filter to just one of the positions to get a single real-valued output.

Later in this notebook, you’ll apply this function to multiple positions of the input to implement the full convolutional operation.

Exercise: Implement conv_single_step(). Hint.

# GRADED FUNCTION: conv_single_step

def conv_single_step(a_slice_prev, W, b):
    """
    Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation 
    of the previous layer.
    
    Arguments:
    a_slice_prev -- slice of input data of shape (f, f, n_C_prev)
    W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)
    b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)
    
    Returns:
    Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data
    """
#記住過濾器上的值和輸入圖片上的小塊上的值相乘之後不用加上bias值，最後相加完之後+bias=output
    ### START CODE HERE ### (≈ 2 lines of code)
    # Element-wise product between a_slice and W. Do not add the bias yet.
    s = np.multiply(a_slice_prev,W)
    # Sum over all entries of the volume s.
    Z = np.sum(s)
    # Add bias b to Z. Cast b to a float() so that Z results in a scalar value.
    Z = Z + b
    ### END CODE HERE ###

    return Z

np.random.seed(1)
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)

Z = conv_single_step(a_slice_prev, W, b)
print("Z =", Z)

Z = [[[-6.99908945]]]

Expected Output:

Z	-6.99908945068

3.3 - Convolutional Neural Networks - Forward pass

In the forward pass, you will take many filters and convolve them on the input. Each ‘convolution’ gives you a 2D matrix output. You will then stack these outputs to get a 3D volume:

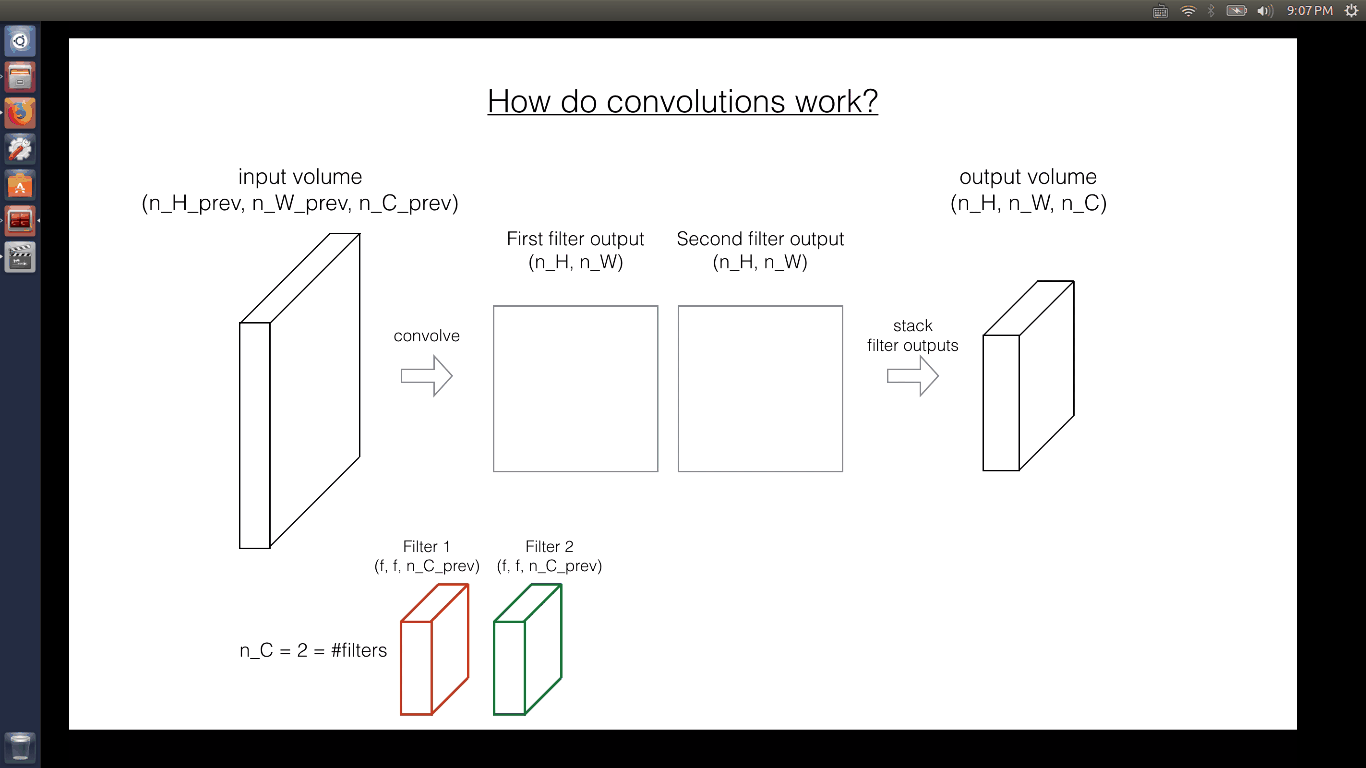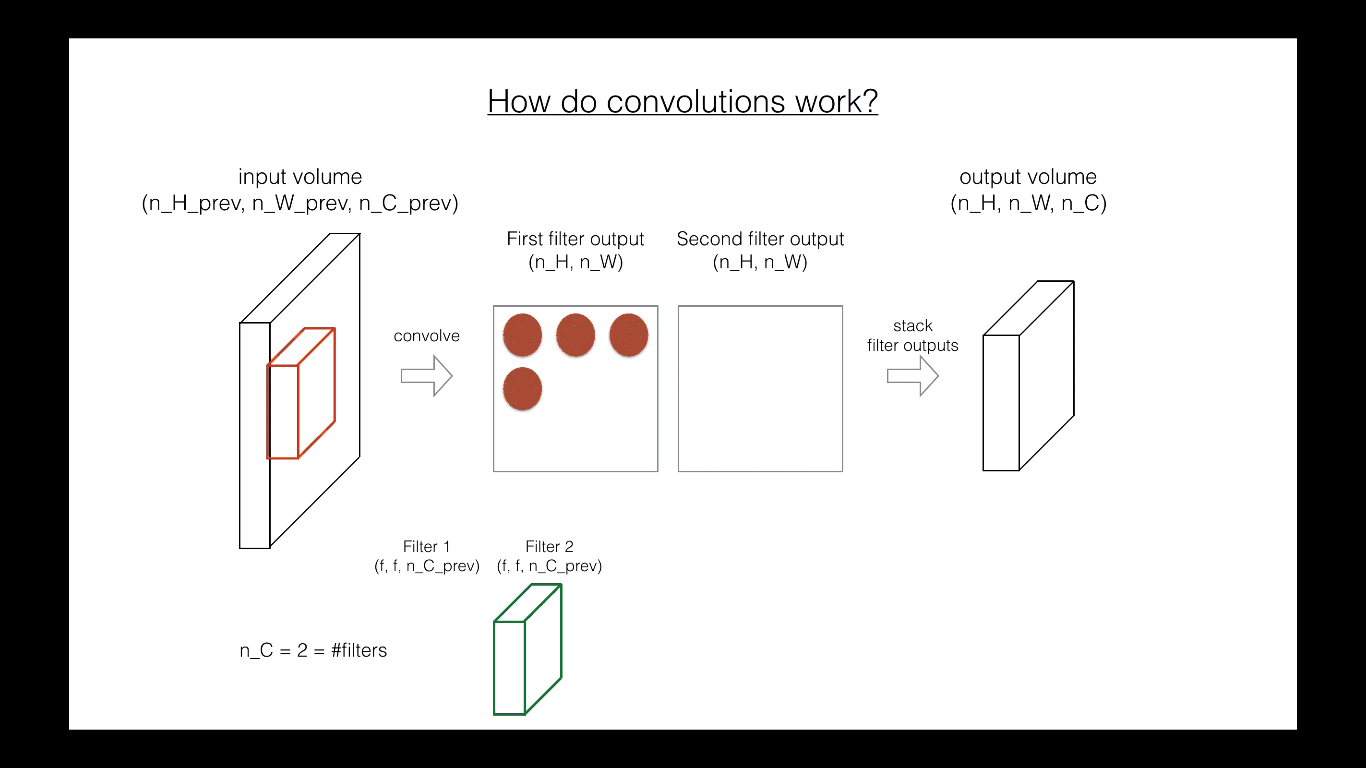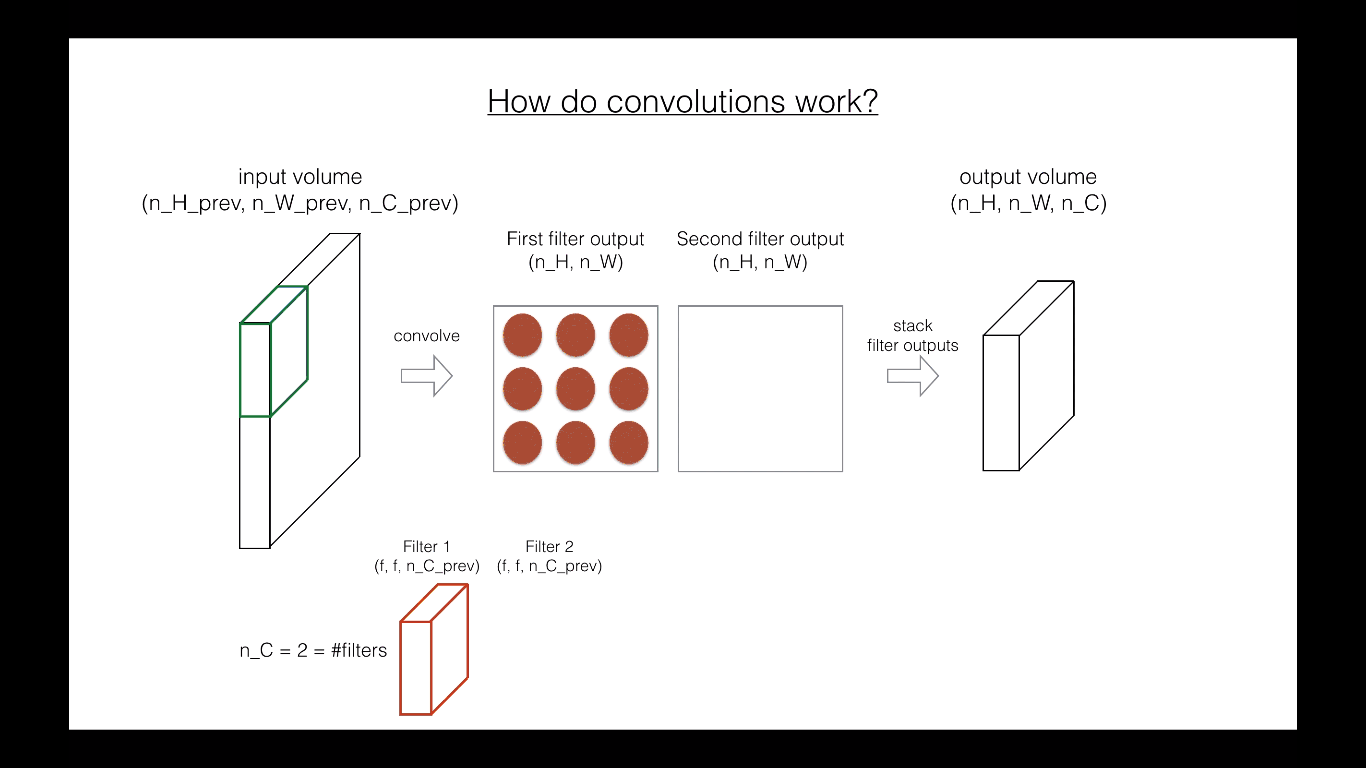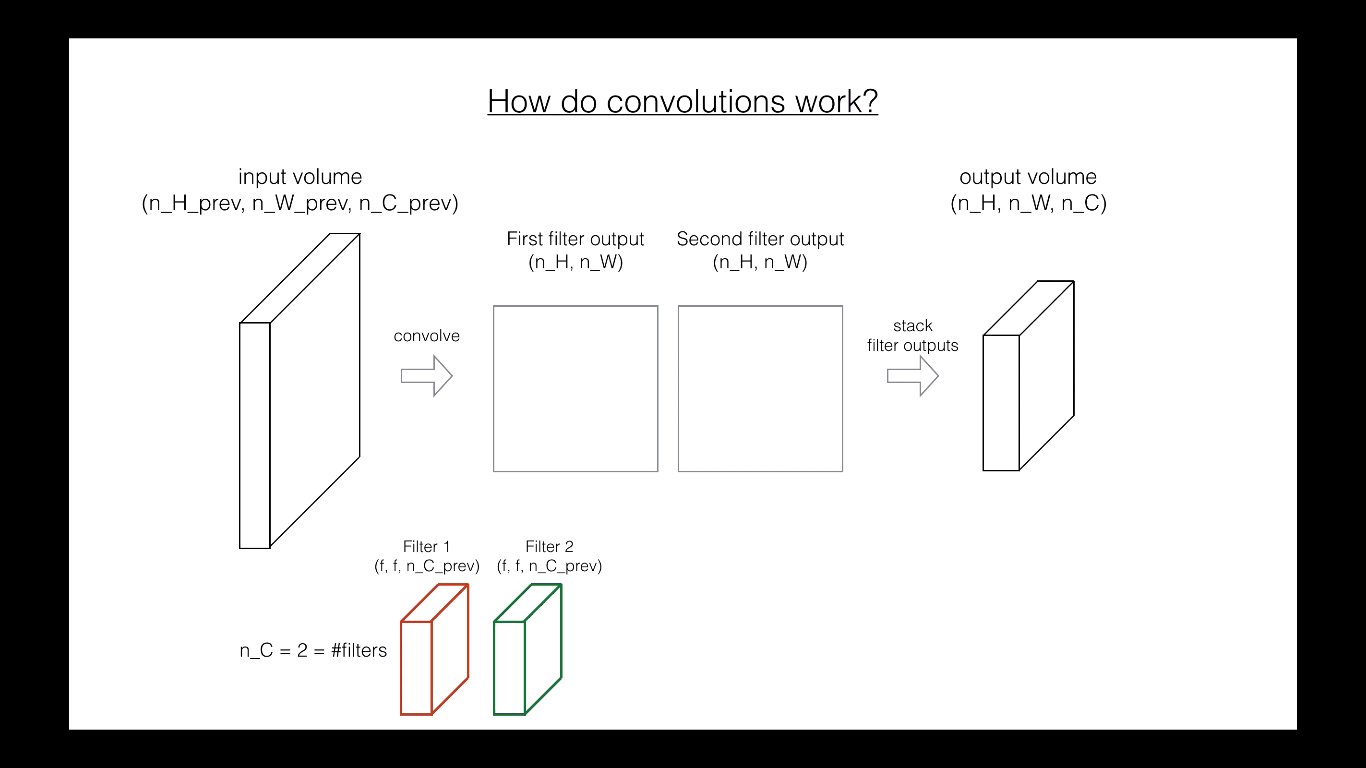
Exercise: Implement the function below to convolve the filters W on an input activation A_prev. This function takes as input A_prev, the activations output by the previous layer (for a batch of m inputs), F filters/weights denoted by W, and a bias vector denoted by b, where each filter has its own (single) bias. Finally you also have access to the hyperparameters dictionary which contains the stride and the padding.

Hint:

1. To select a 2x2 slice at the upper left corner of a matrix “a_prev” (shape (5,5,3)), you would do:

a_slice_prev = a_prev[0:2,0:2,:]

This will be useful when you will define a_slice_prev below, using the start/end indexes you will define.
2. To define a_slice you will need to first define its corners vert_start, vert_end, horiz_start and horiz_end. This figure may be helpful for you to find how each of the corner can be defined using h, w, f and s in the code below.

Figure 3 : Definition of a slice using vertical and horizontal start/end (with a 2x2 filter)
This figure shows only a single channel.

Reminder:
The formulas relating the output shape of the convolution to the input shape is:
$n_H = \lfloor \frac{n_{H_{prev}} - f + 2 \times pad}{stride} \rfloor +1$
$n_W = \lfloor \frac{n_{W_{prev}} - f + 2 \times pad}{stride} \rfloor +1$

相關推薦