03-樹1 樹的同構 （25 point(s)）

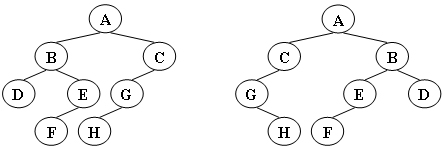
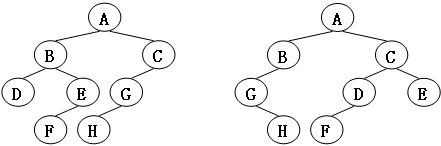
給定兩棵樹T1和T2。如果T1可以通過若干次左右孩子互換就變成T2，則我們稱兩棵樹是“同構”的。例如圖1給出的兩棵樹就是同構的，因為我們把其中一棵樹的結點A、B、G的左右孩子互換後，就得到另外一棵樹。而圖2就不是同構的。

圖1

圖2

現給定兩棵樹，請你判斷它們是否是同構的。

輸入格式:

輸入給出2棵二叉樹樹的資訊。對於每棵樹，首先在一行中給出一個非負整數N (≤10)，即該樹的結點數（此時假設結點從0到N−1編號）；隨後N行，第i行對應編號第i個結點，給出該結點中儲存的1個英文大寫字母、其左孩子結點的編號、右孩子結點的編號。如果孩子結點為空，則在相應位置上給出“-”。給出的資料間用一個空格分隔。注意：題目保證每個結點中儲存的字母是不同的。

輸出格式:

如果兩棵樹是同構的，輸出“Yes”，否則輸出“No”。

輸入樣例1（對應圖1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

輸出樣例1:

Yes

輸入樣例2（對應圖2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

輸出樣例2:

No

emmmmmm這個題，用靜態連結串列實現，搞清楚同構的條件還是挺簡單的，我覺得重要的點就是新載一棵樹的函式怎麼寫，在讀入每行節點的時候要記得在scanf里加一個\n，否則emmm就很操蛋了

還有就是栽樹的函式要返回根節點座標，這個很重要，要用一個檢查的陣列來標記一下

還有還有就是注意一下程式設計習慣，靜態連結串列最好弄成全域性的，在宣告結構的後面加上就行了，還有巨集定義很重要，能夠幫助理解很多東西

#include <cstdio>
#include <iostream>
using namespace std;

typedef char ElemType;
#define Null -1
#define MAXSIZE 10

struct treeNode
{
    ElemType data;
    int left;
    int right;
}tree1[MAXSIZE], tree2[MAXSIZE];
int check[MAXSIZE];          //標記節點是否有指標指向，只為了找出新栽樹的根節點

int buildTree(struct treeNode t[]);
bool isTongGou(int r1, int r2);
int main()
{
    int r1 = buildTree(tree1);
    int r2 = buildTree(tree2);
    if (isTongGou(r1, r2))
        printf("Yes\n");
    else
        printf("No\n");

    return 0;
}

int buildTree(struct treeNode t[])
{
    int n;
    char cr, cl;
    scanf("%d", &n);

    if (n)
    {
        for (int i = 0; i < n; i++)
            check[i] = 0;

        for (int i = 0; i < n; i++) {
            scanf("\n%c %c %c", &t[i].data, &cl, &cr);  //對於%c來說，多行輸入要注意\n，\n也算%c
            if (cl != '-') {
                t[i].left = cl - '0';
                check[t[i].left] = 1;
            } else {
                t[i].left = Null;
            }
            if (cr != '-') {
                t[i].right = cr - '0';
                check[t[i].right] = 1;
            } else {
                t[i].right = Null;
            }
        }
    }

    //尋找根節點座標
    int root = Null;
    for (int i=0; i<n; i++)
        if (check[i] == 0)
        {
            root = i;
            break;
        }
    return root;
}

bool isTongGou(int r1, int r2)
{
    //都為空則同構
    if (r1 == Null && r2 == Null)
        return true;
    //一空一不空
    if ((r1 == Null && r2 != Null) || (r1 != Null && r2 == Null))
        return false;
    //根節點不同
    if (tree1[r1].data != tree2[r2].data)
        return false;
    //左子樹都為空，右子樹不為空
    if ((tree1[r1].left == Null) && (tree2[r2].left == Null))
    {
        return isTongGou(tree1[r1].right, tree2[r2].right);
    }
    //兩棵樹的左兒子都不空而且資料還是一樣的，對左子樹進行遞迴
    if ((tree1[r1].left != Null) && (tree2[r2].left != Null) && tree1[tree1[r1].left].data == tree2[tree2[r2].left].data)
    {
        return (isTongGou(tree1[r1].left, tree2[r2].left) && isTongGou(tree1[r1].right, tree2[r2].right));
    } else   //兩棵樹左兒子都不空，但是資料不一樣，判斷第一棵樹的左（右）和第二顆樹的右（左）是否相同
    {
        return (isTongGou(tree1[r1].left, tree2[r2].right) && isTongGou(tree1[r1].right, tree2[r2].left));
    }
}