影象處理中的卷積總結
一:什麼是卷積
離散卷積的數學公式可以表示為如下形式:
f(x) = - 其中C(k)代表卷積運算元,g(i)代表樣本資料, f(x)代表輸出結果。
舉例如下:
假設g(i)是一個一維的函式,而且代表的樣本數為G = [1,2,3,4,5,6,7,8,9]
假設C(k)是一個一維的卷積運算元, 運算元為C=[-1,0,1]
則輸出結果f(x)可以表示為 F=[1,2,2,2,2,2,2,2,1] //邊界資料未處理
以上只是一維的情況下,當對一幅二維數字影象加以卷積時,其數學意義可以解釋如下:
源影象是作為輸入源資料,處理以後要的影象是卷積輸出結果,卷積運算元作為Filter
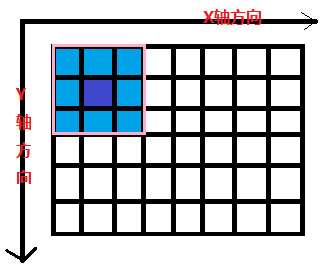
在XY兩個方向上對源影象的每個畫素點實施卷積操作。如圖所示:
粉紅色的方格每次在X/Y前進一個畫素方格,就會產生一個新的輸出畫素,圖中深藍色的代
表要輸出的畫素方格,走完全部的畫素方格,就得到了所有輸出畫素。
圖中,粉紅色的矩陣表示卷積運算元矩陣,黑色表示源影象– 每個方格代表一個畫素點。
二:卷積在數字影象處理中應用
一副數字影象可以看作一個二維空間的離散函式可以表示為f(x, y), 假設有對於二維卷積操
作函式C(u, v) ,則會產生輸出影象g(x, y) = f(x, y) *C(u,v), 利用卷積可以實現對影象模糊處理,邊緣檢測,產生軋花效果的影象。
一個簡單的數字影象卷積處理流程可以如下:
1. 讀取源影象畫素
2. 應用卷積運算元矩陣產生目標影象
3. 對目標影象進行歸一化處理
4. 處理邊界畫素
三使用模板處理影象相關概念:
模板:矩陣方塊,其數學含義是一種卷積運算。
卷積運算:可看作是加權求和的過程,使用到的影象區域中的每個畫素分別於卷積核(權矩陣)的每個元素對應相
乘,所有乘積之和作為區域中心畫素的新值。
卷積核:卷積時使用到的權用一個矩陣表示,該矩陣與使用的影象區域大小相同,其行、列都是奇數,
是一個權矩陣。
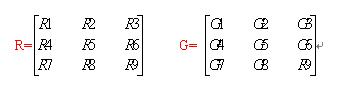
卷積示例:
3 * 3 的畫素區域R與卷積核G的卷積運算:
R5(中心畫素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
四使用模板處理影象的問題:
邊界問題:當處理影象邊界畫素時,卷積核與影象使用區域不能匹配,卷積核的中心與邊界畫素點對應,
卷積運算將出現問題。
處理辦法:
A. 忽略邊界畫素,即處理後的影象將丟掉這些畫素。
B. 保留原邊界畫素,即copy邊界畫素到處理後的影象。
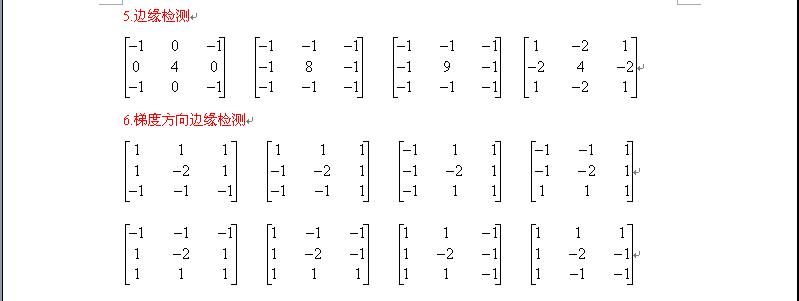
五.常用模板:
六其他
-----------------------------------------------------------------------------------------------------------
以下用$符號表示從負無窮大到正無窮大的積分。
一維卷積:
y(t)=g(k)*x(k)=$g(k)x(t-k)
先把函式x(k)相對於原點反折,然後向右移動距離t,然後兩個函式相乘再積分,就得到了在t處的輸出。對每個t值重複上述過程,就得到了輸出曲線。
二維卷積:
h(x,y)=f(u,v)*g(u,v)=$$f(u,v)g(x-u,y-v)
先將g(u,v)繞其原點旋轉180度,然後平移其原點,u軸上像上平移x, v軸上像上平移y。然後兩個函式相乘積分,得到一個點處的輸出。
在影象中卷積是什麼意思呢,就是影象就是影象f(x),模板是g(x),然後將模版g(x)在模版中移動,每到一個位置,就把f(x)與g(x)的定義域相交的元素進行乘積並且求和,得出新的影象一點,就是被卷積後的影象.模版又稱為卷積核.卷積核做一個矩陣的形狀。由於大多數模板都是對稱的,所以模板不旋轉。
-----------------------------------------------------------------------------------------------------------
相關推薦
影象處理中卷積的實現(TensorFlow和OpenCV)
一、用C解釋原理 假設影象(寬6高4),一個卷積核(寬3高3),如下: unsigned char src[24] ={ 1,2,3,4,5,6, 1,1,1,1,1,1, 2,1,2,1,2,1, 4,5,6,1,2,3};float k
影象處理之——卷積
vImage學習筆記——卷積(Convolution) 卷積(Convolution)是一個常用的影象處理技術,可以改變畫素強度,從而影響周圍其他畫素的強度。卷積的常用技術是建立濾鏡,使用卷積技術,你可以獲取一些流行的影象效果,比如模糊(blur)、銳化(sharpen)及邊緣檢測(edge d
影象處理中的概念總結
本問儘量追求以說人話的方法把所謂的高深概念概括清楚 此篇博文會動態更新 1.Gamma 校正 一句話總結:Gamma 校正其實就是冪指數校正,目的是將灰度較窄的區域拉伸為較寬的區域,如圖,紅框內的輸入區間,對映之後變成了綠框的區間。 2. 直方圖均衡化 一句
影象處理演算法——卷積
本文索引: 一、 什麼是卷積? 在影象處理中,卷積操作指的是使用一個卷積核對影象中的每個畫素進行一系列操作。 卷積核(運算元)是用來做影象處理時的矩陣,影象處理時也稱為掩膜,是與原影象做運算的引數。卷積核通常
(轉載)影象處理(卷積)
卷積公式 解釋 卷積公式是用來求隨機變數和的密度函式(pdf)的計算公式。 定義式: z(t)=x(t)*y(t)= ∫x(m)y(t-m)dm. 已知x,y的pdf,x(t),y(t).現在要求z=x+y的pdf. 我們作變數替顯,令 z=x+y,m=x. 雅可比行列式=1.那麼,z,m聯合密
影象處理和卷積神經網路架構
https://mp.weixin.qq.com/s?__biz=MzA3MzI4MjgzMw==&mid=2650728746&idx=1&sn=61e9cb824501ec7c505eb464e8317915&scene=0#wechat
數字訊號處理中卷積的圖形化動態解釋
目錄(?)[+] 卷積 圖示兩個方形脈衝波的卷積。其中函式 "g" 首先對 反射,接著平移 "t" ,成為 。那麼重疊部份的面積就相當於 "t" 處的卷積,其中橫座標代表待積變數 以及新函式 的自變數 "t" 。 圖示方形脈衝波和指數衰
影象處理中的卷積總結
一:什麼是卷積 離散卷積的數學公式可以表示為如下形式: f(x) = - 其中C(k)代表卷積運算元,g(i)代表樣本資料, f(x)代表輸出結果。 舉例如下: 假設g(i)是一個一維的函式,而且代表的樣本數為G = [1,2,3,4,5,6,7,8,9] 假
影象處理中的卷積
數字訊號處理中卷積 卷積一詞最開始出現在訊號與線性系統中,訊號與線性系統中討論的就是訊號經過一個線性系統以後發生的變化。由於現實情況中常常是一個訊號前一時刻的輸出影響著這一時刻的輸出,所在一般利用系統的單位響應與系統的輸入求卷積,以求得系統的輸出訊號(當然要求這個系統是線
影象處理中的數學原理詳解17——卷積定理及其證明
http://blog.csdn.net/baimafujinji/article/details/484672251.4.5 卷積定理及其證明卷積定理是傅立葉變換滿足的一個重要性質。卷積定理指出,
影象處理中濾波器(卷積核)
本文主要參考來源:影象處理其實很簡單 線性濾波和卷積的關係:線性濾波可以說是影象處理最基本的方法,它可以允許我們對影象進行處理,產生很多不同的效果。做法很簡單。首先,我們有一個二維的濾波器矩陣(有個高大上的名字叫卷積核)和一個要處理的二維影象。然後,對於影象的每一個畫素點,計算它的鄰域畫素和
卷積神經網路及其在影象處理中的應用
一,前言 卷積神經網路(Constitutional Neural Networks, CNN)是在多層神經網路的基礎上發展起來的針對影象分類和識別而特別設計的一種深度學習方法。先回顧一下多層神經網路: 多層神經網路包括一個輸入層和一個輸出層,中間有多個隱藏層。每一
徹底理解數字影象處理中的卷積-以Sobel運算元為例
連結: 原文出處 作者: FreeBlues 概述 卷積在訊號處理領域有極其廣泛的應用, 也有嚴格的物理和數學定義. 本文只討論卷積在數字影象處理中的應用. 在數字影象處理中, 有一種基本的處理方法:線性濾波. 待處理的平面數字影象可被看
影象處理中的卷積運算
卷積是對矩陣中的每一個元素進行的操作,卷積所實現的功能是由其卷積核的形式決定的,卷積核是一個大小固定、有數值引數構成的矩陣,矩陣的中心為參考點(anchor point)或錨點,矩陣的大小稱為核支撐。 卷積計演算法:要計算一個特定點的卷積值,首先將核
影象處理中的卷積與模板
1.使用模板處理影象相關概念: 模板:矩陣方塊,其數學含義是一種卷積運算。 卷積運算:可看作是加權求和的過程,使用到的影象區域中的每個畫素分別與卷積核(權矩陣)的每個元素對應相乘,所有乘積之和作為區域中心畫素的新值。 卷積核:卷積時使用到的權,用一個矩陣表示,該矩陣與使用的
卷積神經網路及影象處理中共享權重、特徵對映等理解
一,前言卷積神經網路(Constitutional Neural Networks, CNN)是在多層神經網路的基礎上發展起來的針對影象分類和識別而特別設計的一種深度學習方法。先回顧一下多層神經網路: 多層神經網路包括一個輸入層和一個輸出層,中間有多個隱藏層。每一層有若干個神
為什麼影象處理中的卷積不反折
卷積是一種積分運算,它可以用來描述線性時不變系統的輸入和輸出的關係:即輸出可以通過輸入和一個表徵系統特性的函式(衝激響應函式)進行卷積運算得到。 以下用$符號表示從負無窮大到正無窮大的積分。
影象處理中的valid卷積與same卷積
#valid卷積 在full卷積的卷積過程中,會遇到$K_{flip}$靠近I的邊界(K矩陣與I矩陣),就會有部分延申到I之外,這時候忽略邊界,只考慮I*完全*覆蓋$K_{flip}$內的值情況,這個的過程就是valid卷積。一個高為H1,寬為W1的矩陣I與高為H2,寬為W2的矩陣K,在H1大於等於H2,W1
理解影象中卷積操作的含義
上文用生動的例子來解釋卷積記載了卷積的含義,現在就來看看卷積在影象處理中的應用吧。(ps:本文大部分內容系轉載大神的部落格,現在csdn強制圖片水印,實在感到很無奈!!!) 數字影象處理中卷積 數字影象是一個二維的離散訊號,對數字影象做卷積操作其實就是利用卷
深度學習中卷積和池化的總結
深度學習中卷積和池化的總結 涉及到padding的設定:https://www.jianshu.com/p/05c4f1621c7e 以及strides=[batch, height, width, channels]中,第一個、第三個引數必須為1的解釋。http://www.itdaa