轉自:https://blog.csdn.net/px_528/article/details/72963977

寫在前面
說到Adaboost，公式與程式碼網上到處都有，《統計學習方法》裡面有詳細的公式原理，Github上面有很多例項，那麼為什麼還要寫這篇文章呢？希望從一種更容易理解的角度，來為大家呈現Adaboost演算法的很多關鍵的細節。

本文中暫時沒有討論其數學公式，一些基本公式可以參考《統計學習方法》。

基本原理
Adaboost演算法基本原理就是將多個弱分類器（弱分類器一般選用單層決策樹）進行合理的結合，使其成為一個強分類器。

Adaboost採用迭代的思想，每次迭代只訓練一個弱分類器，訓練好的弱分類器將參與下一次迭代的使用。也就是說，在第N次迭代中，一共就有N個弱分類器，其中N-1個是以前訓練好的，其各種引數都不再改變，本次訓練第N個分類器。其中弱分類器的關係是第N個弱分類器更可能分對前N-1個弱分類器沒分對的資料，最終分類輸出要看這N個分類器的綜合效果。

弱分類器（單層決策樹）
Adaboost一般使用單層決策樹作為其弱分類器。單層決策樹是決策樹的最簡化版本，只有一個決策點，也就是說，如果訓練資料有多維特徵，單層決策樹也只能選擇其中一維特徵來做決策，並且還有一個關鍵點，決策的閾值也需要考慮。

關於單層決策樹的決策點，來看幾個例子。比如特徵只有一個維度時，可以以小於7的分為一類，標記為+1，大於（等於）7的分為另一類，標記為-1。當然也可以以13作為決策點，決策方向是大於13的分為+1類，小於（等於）13的分為-1類。在單層決策樹中，一共只有一個決策點，所以下圖的兩個決策點不能同時選取。

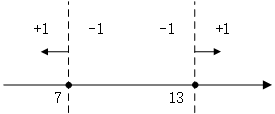
同樣的道理，當特徵有兩個維度時，可以以縱座標7作為決策點，決策方向是小於7分為+1類，大於（等於）7分類-1類。當然還可以以橫座標13作為決策點，決策方向是大於13的分為+1類，小於13的分為-1類。在單層決策樹中，一共只有一個決策點，所以下圖的兩個決策點不能同時選取。

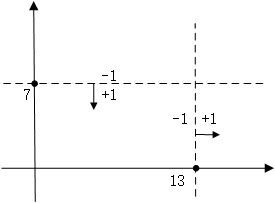
擴充套件到三維、四維、N維都是一樣，在單層決策樹中，一共只有一個決策點，所以只能在其中一個維度中選擇一個合適的決策閾值作為決策點。

關於Adaboost的兩種權重
Adaboost演算法中有兩種權重，一種是資料的權重，另一種是弱分類器的權重。其中，資料的權重主要用於弱分類器尋找其分類誤差最小的決策點

Adaboost資料權重與弱分類器
剛剛已經介紹了單層決策樹的原理，這裡有一個問題，如果訓練資料保持不變，那麼在資料的某個特定維度上單層決策樹找到的最佳決策點每一次必然都是一樣的，為什麼呢？因為單層決策樹是把所有可能的決策點都找了一遍然後選擇了最好的，如果訓練資料不變，那麼每次找到的最好的點當然都是同一個點了。

所以，這裡Adaboost資料權重就派上用場了，所謂“資料的權重主要用於弱分類器尋找其分類誤差最小的點”，其實，在單層決策樹計算誤差時，Adaboost要求其乘上權重，即計算帶權重的誤差。

舉個例子，在以前沒有權重時（其實是平局權重時），一共10個點時，對應每個點的權重都是0.1，分錯1個，錯誤率就加0.1；分錯3個，錯誤率就是0.3。現在，每個點的權重不一樣了，還是10個點，權重依次是[0.01,0.01,0.01,0.01,0.01,0.01, 0.01,0.01,0.01,0.91]，如果分錯了第1一個點，那麼錯誤率是0.01，如果分錯了第3個點，那麼錯誤率是0.01，要是分錯了最後一個點，那麼錯誤率就是0.91。這樣，在選擇決策點的時候自然是要儘量把權重大的點（本例中是最後一個點）分對才能降低誤差率。由此可見，權重分佈影響著單層決策樹決策點的選擇，權重大的點得到更多的關注，權重小的點得到更少的關注。

在Adaboost演算法中，每訓練完一個弱分類器都就會調整權重，上一輪訓練中被誤分類的點的權重會增加，在本輪訓練中，由於權重影響，本輪的弱分類器將更有可能把上一輪的誤分類點分對，如果還是沒有分對，那麼分錯的點的權重將繼續增加，下一個弱分類器將更加關注這個點，儘量將其分對。

這樣，達到“你分不對的我來分”，下一個分類器主要關注上一個分類器沒分對的點，每個分類器都各有側重。

Adaboost分類器的權重
由於Adaboost中若干個分類器的關係是第N個分類器更可能分對第N-1個分類器沒分對的資料，而不能保證以前分對的資料也能同時分對。所以在Adaboost中，每個弱分類器都有各自最關注的點，每個弱分類器都只關注整個資料集的中一部分資料，所以它們必然是共同組合在一起才能發揮出作用。所以最終投票表決時，需要根據弱分類器的權重來進行加權投票，權重大小是根據弱分類器的分類錯誤率計算得出的，總的規律就是弱分類器錯誤率越低，其權重就越高。

圖解Adaboost分類器結構

如圖所示為Adaboost分類器的整體結構。從右到左，可見最終的求和與符號函式，再看到左邊求和之前，圖中的虛線表示不同輪次的迭代效果，第1次迭代時，只有第1行的結構，第2次迭代時，包括第1行與第2行的結構，每次迭代增加一行結構，圖下方的“雲”表示不斷迭代結構的省略。

第i輪迭代要做這麼幾件事：

新增弱分類器WeakClassifier(i)與弱分類器權重alpha(i)
通過資料集data與資料權重W(i)訓練弱分類器WeakClassifier(i)，並得出其分類錯誤率，以此計算出其弱分類器權重alpha(i)
通過加權投票表決的方法，讓所有弱分類器進行加權投票表決的方法得到最終預測輸出，計算最終分類錯誤率，如果最終錯誤率低於設定閾值（比如5%），那麼迭代結束；如果最終錯誤率高於設定閾值，那麼更新資料權重得到W(i+1)
圖解Adaboost加權表決結果
關於最終的加權投票表決，舉幾個例子：
比如在一維特徵時，經過3次迭代，並且知道每次迭代後的弱分類器的決策點與發言權，看看如何實現加權投票表決的。

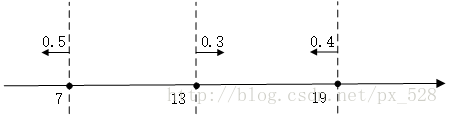
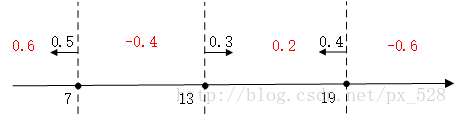
如圖所示，3次迭代後得到了3個決策點，
最左邊的決策點是小於（等於）7的分為+1類，大於7的分為-1類，且分類器的權重為0.5；
中間的決策點是大於（等於）13的分為+1類，小於13分為-1類，權重0.3；
最右邊的決策點是小於（等於19）的分為+1類，大於19分為-1類，權重0.4。
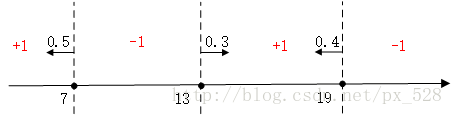
對於最左邊的弱分類器，它的投票表示，小於（等於）7的區域得0.5，大與7得-0.5，同理對於中間的分類器，它的投票表示大於（等於）13的為0.3，小於13分為-0.3，最右邊的投票結果為小於（等於19）的為0.4，大於19分為-0.4，如下圖：

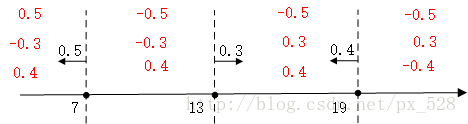
求和可得：

最後進行符號函式轉化即可得到最終分類結果：

更加直觀的，來看一個更復雜的例子。對於二維也是一樣，剛好有一個例項可以分析一下，原始資料分佈如下圖：

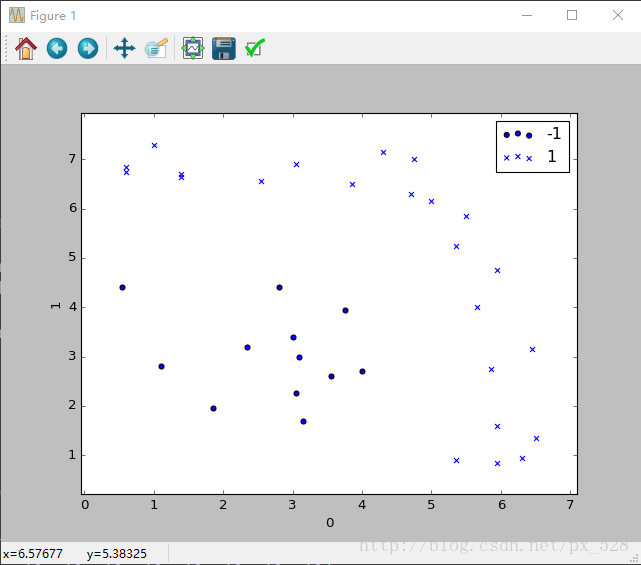
Adaboost分類器試圖把兩類資料分開，執行一下程式，顯示出決策點，如下圖：

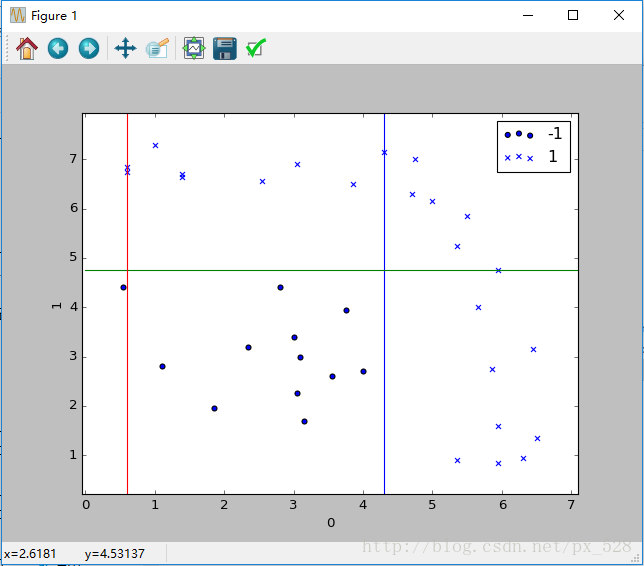
這樣一看，似乎是分開了，不過具體引數是怎樣呢？檢視程式的輸出，可以得到如其決策點與弱分類器權重，在圖中標記出來如下：

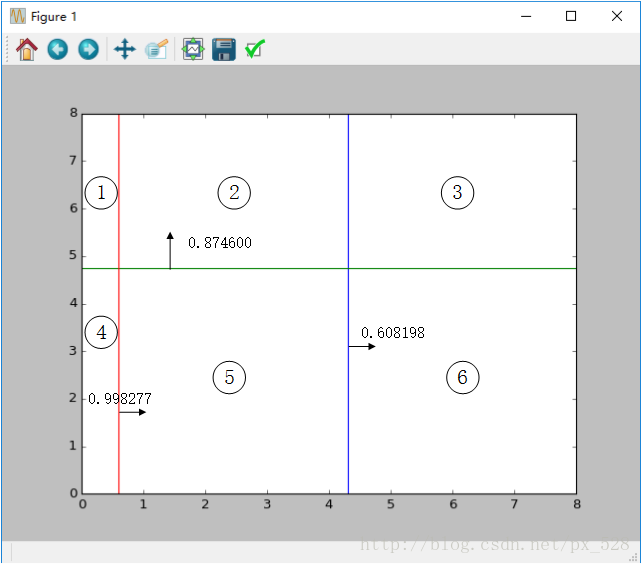
圖中被分成了6分割槽域，每個區域對應的類別就是：
1號：sign(-0.998277+0.874600-0.608198)=-1
2號：sign(+0.998277+0.874600-0.608198)=+1
3號：sign(+0.998277+0.874600+0.608198)=+1
4號：sign(-0.998277-0.874600-0.608198)=-1
5號：sign(+0.998277-0.874600-0.608198)=-1
6號：sign(+0.998277-0.874600+0.608198)=+1
其中sign(x)是符號函式，正數返回1負數返回-1。
最終得到如下效果：

通過這兩個例子，相信你已經明白了Adaboost演算法加權投票時怎麼回事兒了。

總結
說了這麼多，也舉了這麼多例子，就是為了讓你從細節上明白Adaboost的基本原理，博主認為理解Adaboost的兩種權重的關係是理解Adaboost演算法的關鍵所在。