機器學習-Logistic迴歸演算法學習筆記
阿新 • • 發佈:2018-12-16
假設現在有一些資料點,我們用一條直線(或者曲線)對這些點進行擬合,這個擬合過程就稱作迴歸。
利用Logistic迴歸進行分類的主要思想是:根據現有資料對分類邊界線建立迴歸公式,以此進行分類,訓練分類器時的做法就是尋找最佳擬合引數。
- 優點:計算代價不高,易於理解和實現。
- 缺點:容易欠擬合,分類精度可能不高。
- 適用資料型別:數值型和標稱型資料。
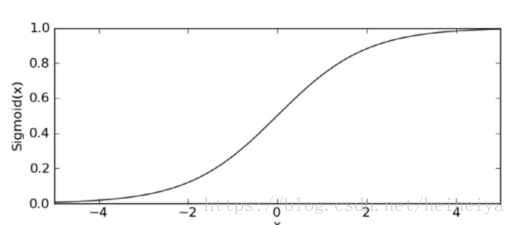
一、Sigmoid函式
我們想要的分類函式應該是能夠接受所有的輸入然後預測出類別。Sigmoid函式就是這樣一個函式。
當x為0時,Sigmoid函式值為0.5。隨著x的增大,對應的Sigmoid值將逼近於1.而隨著x的減小,Sigmoid值將逼近於0。
Sigmoid函式的輸入記為z,由下面的公式得出:
其中,x是分類器的輸入資料,w就是我們需要尋找的分類器的最佳引數。
二、梯度上升法
為了尋找分類器的最佳引數,這裡用到的最優化方法是梯度上升法。
梯度上升法的思想是:要找到某個函式的最大值,最好的方法是沿著該函式的梯度方向尋找。
一直迭代上述公式,直至達到某個停止條件為止。
梯度上升法的虛擬碼如下:
每個迴歸係數初始化為1
重複R次:
計算整個資料集的梯度
使用alpha x gradient更新迴歸係數的向量
返回迴歸係數下面是一個Logistic迴歸梯度上升優化演算法的例子。
首先,從文字檔案中讀取輸入資料:
from numpy import * def loadDataSet(): dataMat = [] labelMat = [] fr = open('testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) labelMat.append(int(lineArr[2])) return dataMat, labelMat
定義Sigmoid函式:
def sigmoid(inX):
return 1.0/(1+exp(-inX))梯度上升優化演算法:
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn)
labelMat = mat(classLabels).transpose()
m ,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n, 1))
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights)
error = (labelMat - h)
weights = weights + alpha * dataMatrix.transpose() * error
return weights呼叫函式,打印出計算得到的優化引數:
dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
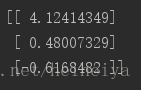
print(weights)輸出:
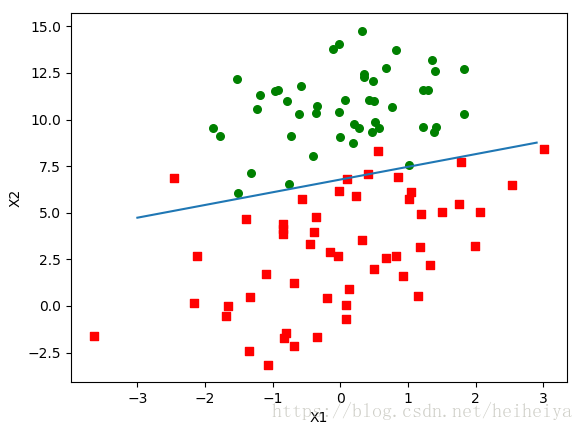
但是這樣看起來沒有直觀的感受,下面來視覺化分類效果。
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat, labelMat = loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1])
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1])
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()plotBestFit(weights.getA())三、隨機梯度上升法
梯度上升法的一個缺點就是每次更新迴歸係數時都需要遍歷整個資料集,這在處理小資料集時尚可,但資料集一旦很大那麼計算複雜度就太高了。
隨機梯度上升法就是對它的一種改進,一次只使用一個樣本點來更新迴歸係數。其虛擬碼如下:
所有迴歸係數初始化為1
對資料集中每個樣本
計算該樣本的梯度
使用alpha × gradient更新迴歸係數值
返回迴歸係數值def stocGradAscent0(dataMatrix, classLabels):
m, n = shape(dataMatrix)
alpha = 0.01
maxCycles = 200
weights = ones(n)
for k in range(maxCycles):
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights呼叫
weights2 = stocGradAscent0(array(dataArr), labelMat)
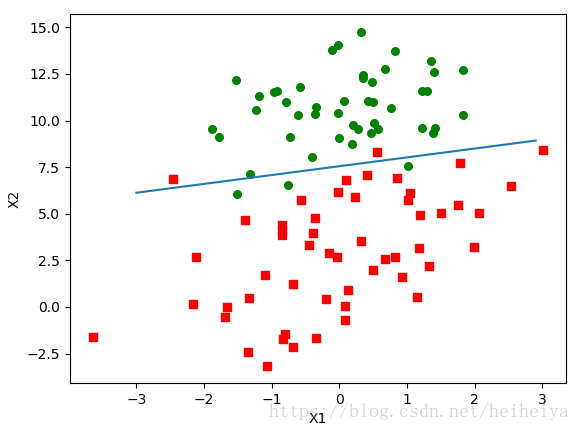
plotBestFit(weights2)四、改進的隨機梯度上升法
但是,在訓練過程中,由於有一些不能正確分類點的存在,導致係數劇烈改變,波動很大。因此對隨機梯度上升法做一些改動。
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m, n = shape(dataMatrix)
weights = ones(n)
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i) + 0.01
randIndex = int(random.uniform(0, len(dataIndex)))
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights首先,alpha在每次迭代時都會改變。其次是通過隨機選取樣本來更新迴歸係數。
weights3 = stocGradAscent1(array(dataArr), labelMat)
plotBestFit(weights3)