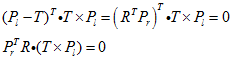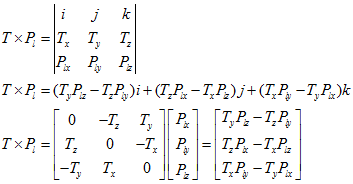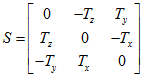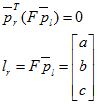對極幾何 本質矩陣 基礎矩陣
對極幾何是檢視幾何理論的基礎，對極幾何（Epipolar Geometry）描述了同一場景兩幅影象之間的視覺幾何關係。
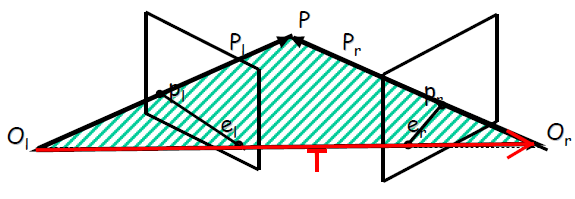
設兩相機的中心分別為Ol和Or，兩影象平面分別為I和
，P為共同視域中的場景空間點，它在兩幅影象平面上的像點分別為pl和pr。對極幾何關係中主要包含以下幾何元素：
極平面：兩個相機座標原點Ol、Or和物體P組成的平面。
極線：極平面和兩個像平面的交線，即和
極點:為右相機原點在左像平面的投影;
為左相機原點在右像平面的投影
我們要研究的極線約束:兩極線上點的對應光系(和
當然也滿足)
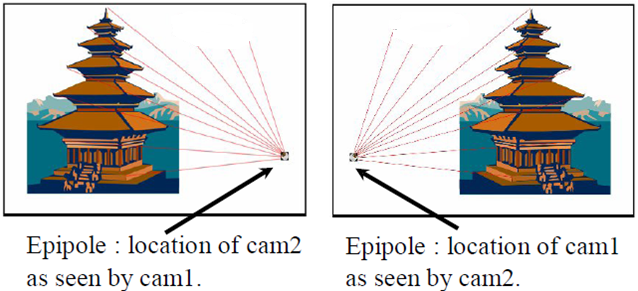
如果有兩個相機,cam1在建築物的左側,cam2在建築物的右側,拍攝得到兩張照片.像平面是無限延伸的,照片只是像平面的一部分.
左側是cam1的像平面，右側是cam2的像平面。
紅線表示相應的對極線，這些對極線滿足一定的幾何約束。
本質矩陣
兩個相機座標系的關係：
是物體P在
相機座標系的位置,
是物體P在
座標系的位置。
相對於
的旋轉矩陣為R,位移為T。則：
由於R是正交矩陣，可以寫成：
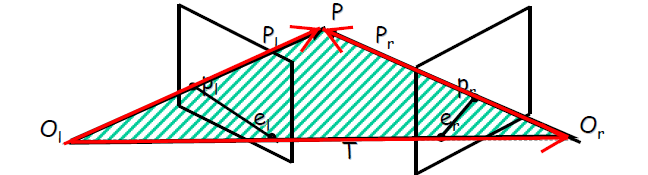
由於三向量共面，如下圖，所以它們的混合積為0.
將叉乘寫成矩陣相乘的形式：
令：
，S是一個秩為2的矩陣，則：
顯然，和
可以通過矩陣E=RS來約束，我們稱E為本質約束(Essential Matrix)。它具有兩個性質：
- 秩為2
- 只依賴於外部引數R和T
基礎矩陣
繼續前面的本質矩陣，結合成像的集合關係：
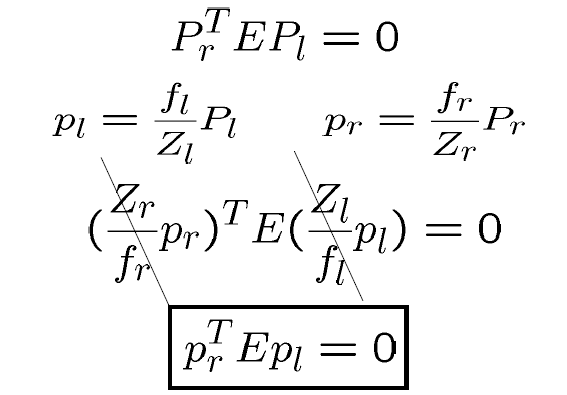
這裡的和
是在單位距離座標系下的位置.如果我們要分析的是影象，需要轉到畫素座標系下，此時：
從而有：
我們稱矩陣F為基礎矩陣：
，性質是：
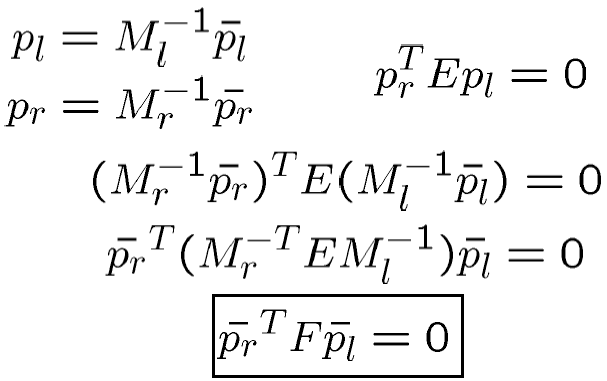
- 秩為2
- 依賴於相機內參和外部引數R和T
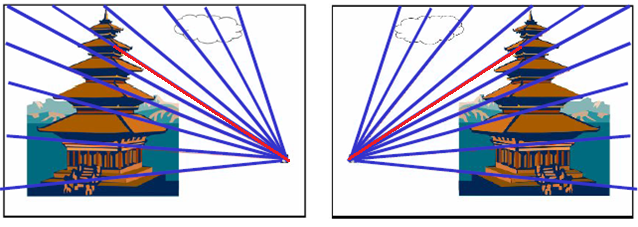
基礎矩陣給出了：在已知一個點和F的情況下，其匹配點的直線約束方程：
直線約束方程為：
進一步分析：
而這裡的F是秩為2的矩陣，所以存在：
和
。
e表示它滿足所有的直線約束，也就是上面圖中那一堆直線的交點，物理意義便是cam2(cam1)在cam1(cam2)的像平面的投影，即極點。
使用SVD分解即可求得極點。