skleran 學習路徑一 線性迴歸模型預測
阿新 • • 發佈:2018-12-18
使用sklearn 裡面的datasets 內建資料集波士頓的房價 來測試這個模型
首先匯入
from sklearn import datasets
loaded_data = datasets.load_boston()#波士頓房價預測
data_x = loaded_data.data
data_y = loaded_data.target
然後使用打出來的資料觀察資料型別,確定資料的的測試集訓練集
# print(loaded_data) # print(data_x) # print(data_y) # print(data_x.shape) # print(data_y.shape) #可以看出有13個特徵值 506個樣本一個標籤預測值
匯入sklearn裡面的linearRegression模型,並且劃分測試集訓練集,建立模型
在這裡from sklearn import model_selection x_train,x_test,y_train,y_test=model_selection.train_test_split(data_x,data_y,test_size=0.25) from sklearn.linear_model import LinearRegression linreg=LinearRegression() linregTr=linreg.fit(x_train,y_train) test_pred=linreg.predict(x_test)插入程式碼片
輸出線性迴歸的截距和係數矩陣
print(linregTr.coef_)
print(linregTr.intercept_)
對模型進行效能分析
在這裡from sklearn import metrics mse_score=metrics.mean_squared_error(y_test,test_pred) print('均方差',mse_score) score_pred=linregTr.score(x_test,y_test) print('準確率',score_pred) from sklearn.model_selection import cross_val_predict predicted=cross_val_predict(linregTr,data_x,data_y,cv=10) print('交叉驗證後的mse_error',metrics.mean_squared_error(data_y,predicted))插入程式碼片
畫圖直觀感受一下模型預測
在這裡import matplotlib.pyplot as plt
fig,axe=plt.subplots()
axe.scatter(y_test,test_pred,color='y',marker='o')
axe.scatter(data_y,predicted,color='b')
axe.scatter(data_y,data_y,color='g',marker='*')
plt.show()插入程式碼片
完整程式碼如下:
在這裡插入from sklearn import datasets
loaded_data = datasets.load_boston()#波士頓房價預測
data_x = loaded_data.data
data_y = loaded_data.target
# print(loaded_data)
# print(data_x)
# print(data_y)
# print(data_x.shape)
# print(data_y.shape)
#可以看出有13個特徵值 506個樣本一個標籤預測值
from sklearn import model_selection
x_train,x_test,y_train,y_test=model_selection.train_test_split(data_x,data_y,test_size=0.25)
from sklearn.linear_model import LinearRegression
linreg=LinearRegression()
linregTr=linreg.fit(x_train,y_train)
test_pred=linreg.predict(x_test)
print(linregTr.coef_)
print(linregTr.intercept_)
from sklearn import metrics
mse_score=metrics.mean_squared_error(y_test,test_pred)
print('均方差',mse_score)
score_pred=linregTr.score(x_test,y_test)
print('準確率',score_pred)
from sklearn.model_selection import cross_val_predict
predicted=cross_val_predict(linregTr,data_x,data_y,cv=10)
print('交叉驗證後的mse_error',metrics.mean_squared_error(data_y,predicted))
import matplotlib.pyplot as plt
fig,axe=plt.subplots()
axe.scatter(y_test,test_pred,color='y',marker='o')
axe.scatter(data_y,predicted,color='b')
axe.scatter(data_y,data_y,color='g',marker='*')
plt.show()程式碼片
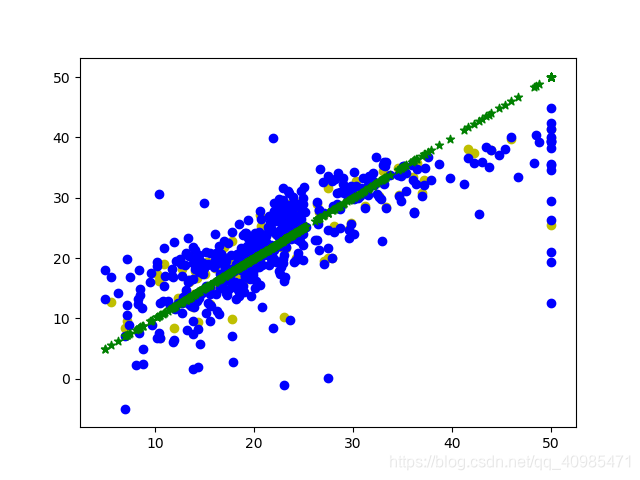
能明顯看出線性迴歸模型對於偏差資料表現異常明顯,所以資料在訓練之前的處理就顯得異常重要,換句話說也就是容易過擬合,此時採用其他的模型更加好一點,但是選擇小資料判斷時,線性迴歸模型絕對是首選
