在一個排列中，如果一對數的前後位置與大小順序相反，即前面的數大於後面的數，那麼它們就稱為一個逆序。一個排列中逆序的總數就稱為這個排列的逆序數。
比如3 4 1 2這個陣列有4對逆序：分別是[3,1] [4,1] [3,2] [4,2]。
本文使用歸併排序來求逆序數。

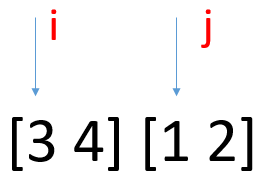
假設歸併排序已經進行到了如上這個狀態，正要把兩個長度為2的有序子序列，合併成一個長度4的有序序列。
i指向前子序列。j指向後子序列。很明顯，當j指向元素小於i指向元素時，就肯定是產生了逆序對了。而逆序對的個數則與i指向元素在前子序列中的位置有關，是從i開始到前子序列的最後元素的個數（包括i和最後元素來統計），通俗地講，就是如果j

def merge(start,former,latter,end,src,des):
    gap = end -start +1
    i = start
    j = latter
    count = 0
    for step in range(gap):
        if (i<=former) and (j<=end):
            if src[i] <= src[j]:
                des[
 
start+step] = src[i]
                i += 1
            else:#只有進入else才代表有逆序對
            	#j元素比i元素小，那麼j肯定也比前子序列中的i後面的元素小
                des[start+step] = src[j]
                j += 1
                count += latter - i#記錄下來前子序列i之後元素個數，包括i
        elif (i<=former):
            des[start+step] =
 
 src[i]
            i += 1
        elif (j<=end):
            des[start+step] = src[j]
            j += 1
    for step in range(gap):
        src[start+step] = des[start+step]
    return count

def merge_sort(start,end,src,des):

    if start < end:
        count = 0
        mid = (start+end)//2
        count += merge_sort(start,mid,src,des)#加上左子序列的逆序對數
        count += merge_sort(mid+1,end,src,des)#加上右子序列的逆序對數
        count += merge(start,mid,mid+1,end,src,des)#再加上左右子序列合併時，發現的逆序對數
        return count
    return 0#遞迴終點返回0

def copy_array(arr):
    return [None for i in range(len(arr))]

arr = [9,8,4,5,7,1,3,6,2]
temp = copy_array(arr)
n = len(arr)

num = merge_sort(0,n-1,arr,temp)
#print(arr)
print(num)

程式碼改自本人另一篇部落格歸併排序 改進歸併，其中的基本歸併排序的程式碼。