2. 程式人生 > >STL系列之九 探索hash set

STL系列之九 探索hash set

阿新 • • 發佈：2018-12-22

Title:        STL系列之九 探索hash_set

Author:     MoreWindows

Blog:       http://blog.csdn.net/MoreWindows

E-mail:     [email protected]

KeyWord:   C++ STL set hash_set 雜湊表 鏈地址法

 

本文將著重探索hash_set比set快速高效的原因，閱讀本文前，推薦先閱讀本文的姊妹篇《STL系列之六 set與hash_set》

一．hash_set之基石——雜湊表

    hash_set的底層資料結構是雜湊表，因此要深入瞭解hash_set，必須先分析雜湊表。雜湊表是根據關鍵碼值(Key-Value)而直接進行訪問的資料結構，它用雜湊函式處理資料得到關鍵碼值，關鍵碼值對應表中一個特定位置再由應該位置來訪問記錄，這樣可以在時間複雜性度為O(1)內訪問到資料。但是很有可能出現多個數據經雜湊函式處理後得到同一個關鍵碼——這就產生了衝突，解決衝突的方法也有很多，各大資料結構教材及考研輔導書上都會介紹大把方法。這裡採用最方便最有效的一種——鏈地址法，當有衝突發生時將具同一關鍵碼的資料組成一個連結串列。下圖展示了鏈地址法的使用：

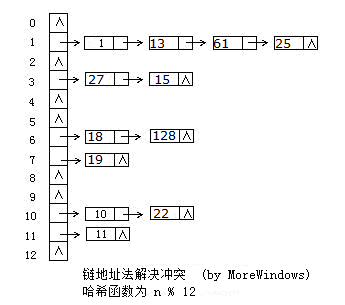
二．簡化版的hash_table

    按照上面的分析和圖示，並參考《程式設計珠璣》第15章中雜湊表的實現，不難寫出一個簡單的雜湊表，我們稱之為簡化版hash_table。該雜湊表由一個指標陣列組成，陣列中每個元素都是連結串列的表頭指標，程式分為hash_table.h，hash_table.cpp和main.cpp。

1.hash_table.h

#pragma once
#define NULL 0
//簡化版hash_table 
//by MoreWindows( http://blog.csdn.net/MoreWindows )
struct
 
 Node
{
	int val;
	Node *next;
	Node(int n)
	{
		this->val = n;
		this->next = NULL;
	}
};
class hash_table
{
public:
	hash_table(const int ntablesize);
	~hash_table();
	bool insert(int n);
	void insert(int *pFirst, int *pLast);
	bool find(int n);
	int  size();
	int HashFun(int n);
public:
	int      m_nTableSize;
	int      m_nTableDataCount;
	Node**   m_ppTable;
};

2.hash_table.cpp

//簡化版hash_table
//by MoreWindows( http://blog.csdn.net/MoreWindows )
#include "hash_table.h"
#include <malloc.h>
#include <memory.h>
hash_table::hash_table(const int ntablesize)
{
	m_nTableSize = ntablesize;
	m_ppTable = (Node**)malloc(sizeof(Node*) * m_nTableSize);
	if (m_ppTable == NULL)
		return ;
	m_nTableDataCount = 0;
	memset(m_ppTable, 0, sizeof(Node*) * m_nTableSize);
}
hash_table::~hash_table()
{
	free(m_ppTable);
	m_ppTable = NULL;
	m_nTableDataCount = 0;
	m_nTableSize = 0;
}
int inline hash_table::HashFun(int n) 
{
	return (n ^ 0xdeadbeef) % m_nTableSize;
}
int hash_table::size()
{
	return m_nTableDataCount;
}
bool hash_table::insert(int n)
{
	int key = HashFun(n);
	//在該連結串列中查詢該數是否已經存在
	for (Node *p = m_ppTable[key]; p != NULL; p = p->next)
		if (p->val == n)
			return true;
	//在連結串列的頭部插入
	Node *pNode = new Node(n);
	if (pNode == NULL)
		return false;
	pNode->next = m_ppTable[key];
	m_ppTable[key] = pNode;
	m_nTableDataCount++;
	return true;
}
bool hash_table::find(int n)
{
	int key = HashFun(n);
	for (Node *pNode = m_ppTable[key]; pNode != NULL; pNode = pNode->next)
		if (pNode->val == n)
			return true;
	return false;
}
void hash_table::insert(int *pFirst, int *pLast)
{
	for (int *p = pFirst; p != pLast; p++)
		this->insert(*p);
}

3．main.cpp

 在main.cpp中，對set、hash_set、簡化版hash_table作一個性能測試，測試環境為Win7+VS2008的Release設定（下同）。

//測試set，hash_set及簡化版hash_table
// by MoreWindows( http://blog.csdn.net/MoreWindows )
#include <set>
#include <hash_set>
#include "hash_table.h"
#include <iostream>
#include <ctime>
#include <cstdio>
#include <cstdlib>
using namespace std;
using namespace stdext;  //hash_set
void PrintfContainerElapseTime(char *pszContainerName, char *pszOperator, long lElapsetime)
{
	printf("%s 的 %s操作 用時 %d毫秒\n", pszContainerName, pszOperator, lElapsetime);
}
// MAXN個數據 MAXQUERY次查詢
const int MAXN = 5000000, MAXQUERY = 5000000;
int a[MAXN], query[MAXQUERY];
int main()
{
	printf("set VS hash_set VS hash_table(簡化版) 效能測試\n");
	printf("資料容量 %d個 查詢次數 %d次\n", MAXN, MAXQUERY);
	const int MAXNUM = MAXN * 4;
	const int MAXQUERYNUM = MAXN * 4;
	printf("容器中資料範圍 [0, %d) 查詢資料範圍[0, %d)\n", MAXNUM, MAXQUERYNUM);
	printf("--by MoreWindows( http://blog.csdn.net/MoreWindows ) --\n\n");
	
	//隨機生成在[0, MAXNUM)範圍內的MAXN個數
	int i;
	srand((unsigned int)time(NULL));
	for (i = 0; i < MAXN; ++i)
		a[i] = (rand() * rand()) % MAXNUM;
	//隨機生成在[0, MAXQUERYNUM)範圍內的MAXQUERY個數
	srand((unsigned int)time(NULL));
	for (i = 0; i < MAXQUERY; ++i)
		query[i] = (rand() * rand()) % MAXQUERYNUM;

	set<int>       nset;
	hash_set<int>  nhashset;
	hash_table   nhashtable(MAXN + 123);
	clock_t  clockBegin, clockEnd;

	//insert
	printf("-----插入資料-----------\n");
	clockBegin = clock();	 
	nset.insert(a, a + MAXN); 
	clockEnd = clock();
	printf("set中有資料%d個\n", nset.size());
	PrintfContainerElapseTime("set", "insert", clockEnd - clockBegin);

	clockBegin = clock();  
	nhashset.insert(a, a + MAXN); 
	clockEnd = clock();
	printf("hash_set中有資料%d個\n", nhashset.size());
	PrintfContainerElapseTime("hash_set", "insert", clockEnd - clockBegin);

	clockBegin = clock();
	for (i = 0; i < MAXN; i++)
		nhashtable.insert(a[i]); 
	clockEnd = clock();
	printf("hash_table中有資料%d個\n", nhashtable.size());
	PrintfContainerElapseTime("Hash_table", "insert", clockEnd - clockBegin);

	//find
	printf("-----查詢資料-----------\n");
	int nFindSucceedCount, nFindFailedCount; 
	nFindSucceedCount = nFindFailedCount = 0;
	clockBegin = clock(); 
	for (i = 0; i < MAXQUERY; ++i)
		if (nset.find(query[i]) != nset.end())
			++nFindSucceedCount;
		else
			++nFindFailedCount;
	clockEnd = clock();
	PrintfContainerElapseTime("set", "find", clockEnd - clockBegin);
	printf("查詢成功次數： %d    查詢失敗次數： %d\n", nFindSucceedCount, nFindFailedCount);
	
	nFindSucceedCount = nFindFailedCount = 0;
	clockBegin = clock();  
	for (i = 0; i < MAXQUERY; ++i)
		if (nhashset.find(query[i]) != nhashset.end())
			++nFindSucceedCount;
		else
			++nFindFailedCount;
	clockEnd = clock();
	PrintfContainerElapseTime("hash_set", "find", clockEnd - clockBegin);
	printf("查詢成功次數： %d    查詢失敗次數： %d\n", nFindSucceedCount, nFindFailedCount);

	nFindSucceedCount = nFindFailedCount = 0;
	clockBegin = clock();  
	for (i = 0; i < MAXQUERY; ++i)
		if (nhashtable.find(query[i]))
			++nFindSucceedCount;
		else
			++nFindFailedCount;
	clockEnd = clock();
	PrintfContainerElapseTime("hash_table", "find", clockEnd - clockBegin);
	printf("查詢成功次數： %d    查詢失敗次數： %d\n", nFindSucceedCount, nFindFailedCount);
	return 0;
}

在資料量為500萬時測試結果如下：

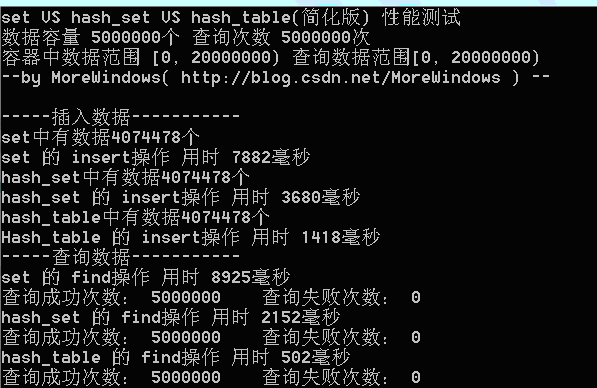
從程式執行結果可以發現，我們自己實現的hash_table（簡化版）在插入和查詢的效率要遠高於set。為了進一步分析，最好能統計hash_table中的各個連結串列的長度情況，這樣可以有效的瞭解平均每次查詢要訪問多少個數據。寫出統計hash_table各連結串列長度的函式如下：

// by MoreWindows( http://blog.csdn.net/MoreWindows )
void StatisticHashTable(hash_table &ht)
{
	const int MAXLISTLINE = 100;
	int i, a[MAXLISTLINE], nExtendListNum;
	nExtendListNum = 0;
	memset(a, 0, sizeof(a[0]) * MAXLISTLINE);
	for (i = 0; i < ht.m_nTableSize; i++)
	{
		int sum = 0;
		for (Node *p = ht.m_ppTable[i]; p != NULL; p = p->next)
			++sum;
		if (sum >= MAXLISTLINE)
			nExtendListNum++;
		else
			a[sum]++;
	}
	printf("hash_table中連結串列長度統計：\n");
	for (i = 0; i < MAXLISTLINE; i++)
		if (a[i] > 0)
		{
			printf("   長度為%d的連結串列有%d個 這些連結串列中資料佔總資料的%.2lf%%\n", i, a[i], (a[i] * i * 100.0) / ht.size());
		}
		printf("   長度超過%d的連結串列有%d個\n", MAXLISTLINE, nExtendListNum);
}

用此段程式碼得到連結串列長度的統計結果：

可以發現在hash_table中最長的連結串列也只有5個元素，長度為1和長度為2的連結串列中的資料佔全部資料的89%以上。因此絕大數查詢將僅僅訪問雜湊表1次到2次。這樣的查詢效率當然會比set（內部使用紅黑樹——類似於二叉平衡樹）高的多。有了這個圖示，無疑已經可以證明hash_set會比set快速高效了。但hash_set還可以動態的增加表的大小，因此我們再實現一個表大小可增加的hash_table。

三．強化版hash_table

    首先來看看VS2008中hash_set是如何實現動態的增加表的大小，hash_set是在hash_set.h中宣告的，在hash_set.h中可以發現hash_set是繼承_Hash類的，hash_set本身並沒有太多的程式碼，只是對_Hash作了進一步的封裝，這種做法在STL中非常常見，如stack棧和queue單向佇列都是以deque雙向佇列作底層資料結構再加一層封裝。

_Hash類的定義和實現都在xhash.h類中，微軟對_Hash類的第一句註釋如下——

        hash table -- list with vector of iterators for quick access。

哈哈，這句話說的非常明白。這說明_Hash實際上就是由vector和list組成雜湊表。再閱讀下程式碼可以發現_Hash類增加空間由_Grow()函式完成，當空間不足時就倍增，並且表中原有資料都要重新計算hash值以確定新的位置。

知道了_Hash類是如何運作的，下面就來考慮如何實現強化版的hash_table。當然有二個地方還可以改進：

1．_Hash類使用的list為雙向連結串列，但在在雜湊表中使用普通的單鏈表就可以了。因此使用STL中的vector再加入《STL系列之八 slist單鏈表》一文中的slist來實現強化版的hash_table。

2．在空間分配上使用了一個近似於倍增的素數表，最開始取第一個素數，當空間不足時就使用下一個素數。經過實際測試這種效果要比倍增法高效一些。

在這二個改進之上的強化版的hash_table程式碼如下：

//使用vector< slist<T> >為容器的hash_table
// by MoreWindows( http://blog.csdn.net/MoreWindows )
template< class T, class container = vector<slist<T>> >
class hash_table
{
public:
	hash_table();
	hash_table(const int ntablesize);
	~hash_table();
	void clear();
	bool insert(T &n);
	void insert(T *pFirst, T *pLast);
	bool erase(T &n);
	void resize(int nNewTableSize);
	bool find(T &n);
	int size();
	int HashFun(T &n);
private:
	static int findNextPrime(int curPrime);
public:
	int         m_nDataCount;
	int         m_nTableSize;
	container   m_Table;
	static const unsigned int m_primes[50];
};
//素數表
template< class T, class container>
const unsigned int hash_table<T, container>::m_primes[50] = {
	53, 97, 193, 389, 769, 1453, 3079, 6151, 1289, 24593, 49157, 98317, 
	196613, 393241, 786433, 1572869, 3145739, 6291469, 12582917, 
	25165843, 50331653, 100663319, 201326611, -1
};
template< class T, class container>
int inline hash_table<T, container>::HashFun(T &n)
{
	return (n ^ 0xdeadbeef) % m_nTableSize;
}
template< class T, class container>
hash_table<T, container>::hash_table()
{
	m_nDataCount = 0;
	m_nTableSize = m_primes[0];
	m_Table.resize(m_nTableSize);
}
template< class T, class container>
hash_table<T, container>::hash_table(const int ntablesize)
{
	m_nDataCount = 0;
	m_nTableSize = ntablesize;
	m_Table.resize(m_nTableSize);
}
template< class T, class container>
hash_table<T, container>::~hash_table()
{
	clear();
}
template< class T, class container>
void hash_table<T, container>::clear()
{
	for (int i = 0; i < m_nTableSize; i++)
		m_Table[i].clear();
	m_nDataCount = 0;
}
template< class T, class container>
bool hash_table<T, container>::insert(T &n)
{
	int key = HashFun(n);
	if (!m_Table[key].find(n))
	{
		m_nDataCount++;
		m_Table[key].push_front(n);
		if (m_nDataCount >= m_nTableSize)
			resize(findNextPrime(m_nTableSize));
	}
	return true;
}
template< class T, class container>
bool hash_table<T, container>::erase(T &n)
{
	int key = HashFun(n);
	if (m_Table[key].remove(n))
	{
		m_nDataCount--;
		return true;
	}
	else
	{
		return false;
	}
}
template< class T, class container>
void hash_table<T, container>::insert(T *pFirst, T *pLast)
{
	for (T *p = pFirst; p != pLast; p++)
		this->insert(*p);
}
template< class T, class container>
void hash_table<T, container>::resize(int nNewTableSize)
{
	if (nNewTableSize <= m_nTableSize)
		return;
	int nOldTableSize = m_nTableSize;
	m_nTableSize = nNewTableSize;
	container tempTable(m_nTableSize); //建立一個更大的表
	for (int i = 0; i < nOldTableSize; i++)//將原表中資料重新插入到新表中
	{
		Node<T> *cur = m_Table[i].m_head;
		while (cur != NULL)
		{
			int key = HashFun(cur->val);
			Node<T> *pNext = cur->next;
			cur->next = tempTable[key].m_head;
			tempTable[key].m_head = cur;
			cur = pNext;
		}
		m_Table[i].m_head = NULL;
	}
	m_Table.swap(tempTable);
}
template< class T, class container>
int hash_table<T, container>::size()
{
	return m_nDataCount;
}
template< class T, class container>
bool hash_table<T, container>::find(T &n)
{
	int key = HashFun(n);
	return m_Table[key].find(n);
}
//在素數表中找到比當前數大的最小數
template< class T, class container>
int hash_table<T, container>::findNextPrime(int curPrime)
{
	unsigned int *pStart = (unsigned int *)m_primes;
	while (*pStart <= curPrime)
		++pStart;
	return *pStart;
}

下面再對set、hash_set、強化版hash_table的效能測試：

測試結果一（資料量500萬）：

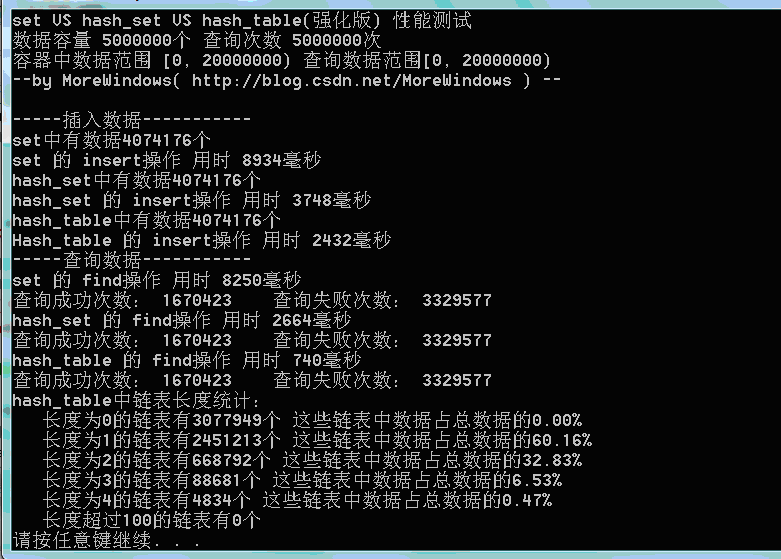
測試結果二（資料量1千萬）：

測試結果三（資料量1千萬）：

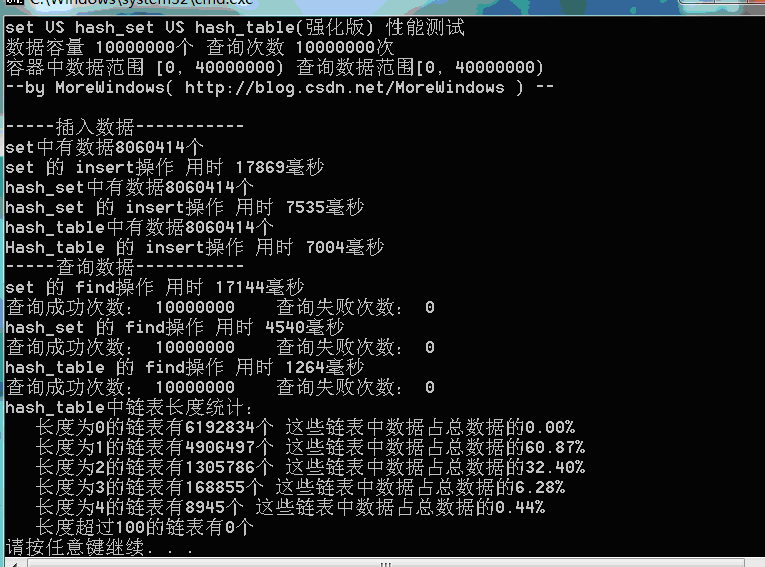
可以看出，由於強化版hash_table的雜湊表在增加表空間大小時會花費額外的一些時間，所以插入資料的用時與STL提供的hash_set用時相差不多了。但查詢還是比hash_set要快的一些。

四．結語

從簡化版到強化版的hash_table，我們不僅知道了hash_set底層資料結構——雜湊表的運作機制，還知道了如何實現大小動態變化的雜湊表。達到了本文讓讀者瞭解hash_set快速高效的原因。當然本文所給hash_table距真正的hash_set還有不小的距離，有興趣的讀者可以進一步改進。

此外，本文所示範的雜湊表也與最近流行的NoSql資料庫頗有淵源， NoSql資料庫也是通過Key-Value方式來訪問資料的（訪問資料的方式上非常類似雜湊表），其查詢效率與傳統的資料庫相比也正如本文中hast_set與set的比較。正因為NoSql資料庫在基礎資料結構上的天然優勢，所以它完全可以支援海量資料的查詢修改且對操作效能要求很高場合如微博等。

 

 

轉載請標明出處，原文地址：http://blog.csdn.net/morewindows/article/details/7330323

 

 

再分享一下我老師大神的人工智慧教程吧。零基礎！通俗易懂！風趣幽默！希望你也加入到我們人工智慧的隊伍中來！https://www.cnblogs.com/captainbed

相關推薦

STL系列之九 探索hash set

Title:        STL系列之九 探索hash_set Author:     MoreWindows Blog:       

STL系列之六 set與hash set

STL系列之六 set與hash_set set和hash_set是STL中比較重要的容器，有必要對其進行深入瞭解。在STL中，set是以紅黑樹（RB-tree）作為底層資料結構的，hash_set是以Hash table（雜湊表）作為底層資料結構的。set可以在時間複雜度為O(logN)情況下插入

【C++】STL常用容器總結之九：集合set

10、集合set Map容器是鍵值對的集合，而set容器只是單純的鍵的集合，當只想知道一個值是否存在時，使用set容器是最合適的。在set中，所有元素都會根據其鍵值被自動排序，同時set中不允許兩個元素有相同的鍵值。 1、set容器的一些操作 Set容

Exchange 2013系列之九：OWA重定向

Windows Server Exchange AD 目前我們的Exchange 服務器已經部署完成了，但對於用戶來說，OWA的訪問鏈接還是太繁瑣，且並沒有訪問統一網站，那有沒有什麽辦法可以解決這一問題呢？任務：將https://mail.windows.com 重定向至 https://exch

skyfans之每天一個Liunx命令系列之九：dmidecode

今天我們繼續來學習PERFORMANCE MONITORING AND STATISTICS（效能監測與統計），今天學習的是什麼命令呢，那就是dmidecode（通過BIOS檢視硬體資訊） Ready Go!!! 老規矩 dmidecode --help -d：(default:/

STL系列之四 heap 堆

下面再介紹STL中與堆相關的4個函式——建立堆make_heap()，在堆中新增資料push_heap()，在堆中刪除資料pop_heap()和堆排序sort_heap()： 標頭檔案 #include <algorithm> 下面的_First與_Last為可以隨機訪問的迭代器（指

STL系列之十 全排列(百度迅雷筆試題)

全排列在筆試面試中很熱門，因為它難度適中，既可以考察遞迴實現，又能進一步考察非遞迴的實現，便於區分出考生的水平。所以在百度和迅雷的校園招聘以及程式設計師和軟體設計師的考試中都考到了，因此本文對全排列作下總結幫助大家更好的學習和理解。對本文有任何補充之處，歡迎大家指出。首先來看

STL系列之五 priority queue 優先順序佇列

priority_queue 優先順序佇列是一個擁有權值概念的單向佇列queue，在這個佇列中，所有元素是按優先順序排列的（也可以認為queue是個按進入佇列的先後做為優先順序的優先順序佇列——先進入佇列的元素優先權要高於後進入佇列的元素）。在計算機作業系統中，優先順序佇列的使用是相當頻繁的，進執行緒排

STL系列之七 快速計算x的n次冪 power 的實現

                計算x的n次冪最簡單直接的方法就是相乘n次，很容易寫出程式：//計算x^n 直接乘n次 by MoreWindows( http://blog.csdn.net/MoreWindows )int power1(int x, unsigned int n){ int result

STL系列之三 queue 單向佇列

//VS2008中 queue的定義 MoreWindows整理(http://blog.csdn.net/MoreWindows)template<class _Ty, class _Container = deque<_Ty> >class queue{ // FIFO queue

IT職場人生系列之九 消費觀（攢錢，繼續教育，買房）

                本文是IT職場人生系列的第九篇。前不久幾個朋友去海南玩，因為一位年輕的同事正好在附近出差，就一起去了。這樣的一次旅遊，幾乎會花掉她大半個月的工資，所以引發了對金錢觀的思考，簡單而言，就是：錢該怎麼花？整體比較亂，用幾個問題串起來。每個人的環境和經歷不同，因此只可說是自己回顧及環

STL系列之二 stack棧

                棧（statck）這種資料結構在計算機中是相當出名的。棧中的資料是先進後出的（First In Last Out, FILO）。棧只有一個出口，允許新增元素（只能在棧頂上增加）、移出元素（只能移出棧頂元素）、取得棧頂元素等操作。在STL中，棧是以別的容器作為底部結構，再將介面改

白話經典算法系列之九 從歸併排序到數列的逆序數對（微軟筆試題）

首先來看看原題   微軟2010年筆試題 在一個排列中，如果一對數的前後位置與大小順序相反，即前面的數大於後面的數，那麼它們就稱為一個逆序數對。一個排列中逆序的總數就稱為這個排列的逆序數。如{2，4，3，1}中，2和1，4和3，4和1，3和1是逆序數對，因此整個陣列的逆序數對個數為

Docker系列之九：Docker用於持續整合，構建Jenkins和Docker伺服器

系列連結 Docker系列之一：Docker介紹及在Ubuntu上安裝 Docker系列之二：Docker 入門 Docker系列之三：使用Docker映象和倉庫 Docker系列之四：Dockerfile的使用 Docker系列之五：Volume 卷的使用——以Redis為例

ElasticStack系列之九 & master、data 和 client 節點

　　在生產環境下，如果不修改elasticsearch節點的角色資訊，在高資料量，高併發的場景下叢集容易出現腦裂等問題。 　　預設情況下，elasticsearch 叢集中每個節點都有成為主節點的資格，也都儲存資料，還可以提供查詢服務。這些功能是由兩個屬性控制的。 　　　　1. node.master 　　　

STL系列之七 快速計算x的n次冪 power 的實現

計算x的n次冪最簡單直接的方法就是相乘n次，很容易寫出程式： //計算x^n 直接乘n次 by MoreWindows( http://blog.csdn.net/MoreWindows ) int power1(int x, unsigned int n) { int result = 1;

算法系列之九：計算幾何與圖形學有關的幾種常用演算法（二）

3.6 用向量的叉積判斷直線段是否有交        向量叉積計算的另一個常用用途是直線段求交。求交演算法是計算機圖形學的核心演算法，也是體現速度和穩定性的重要標誌，高效並且穩定的求交演算法是任何一個CAD軟體都必需要重點關注的。求交包含兩層概念，一個是判斷是否相交，另一個是

Android實用檢視動畫及工具系列之九：漂亮的圖片選擇器，高效能防崩潰圖片選擇工具

public class MainActivity extends AppCompatActivity { private Button btn1, btn2; private TextView tv1; private ArrayList<String> path =

【C++ STL學習之五】容器set和multiset

一、set和multiset基礎 set和multiset會根據特定的排序準則，自動將元素進行排序。不同的是後者允許元素重複而前者不允許。 需要包含標頭檔案： #include <set> set和multiset都是定義在std空間裡的類模板： templ

強化學習系列之九:Deep Q Network (DQN)

      我們終於來到了深度強化學習。 1. 強化學習和深度學習結合       機器學習=目標+表示+優化。目標層面的工作關心應該學習到什麼樣的模型，強化學習應該學習到使得激勵函式最大的模型。表示方面的工作關心資料表示成什麼樣有利於學習，深度學習是最近幾年興