組合數C(n,m)的求法總結,盧卡斯定理
阿新 • • 發佈:2018-12-24
組合數C(n,k)的求法總結
與組合數有關的兩個最重要內容是楊輝三角和二項式定理。
楊輝三角前10行如下所示:
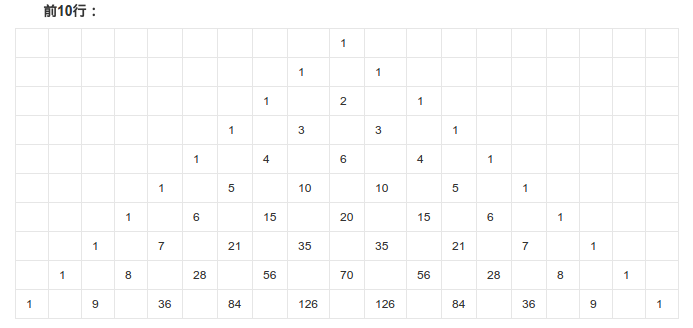
另一方面,將(a+b)^n展開,係數正好和楊輝三角一致。 一般有(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)b+...+C(n,n)b^n。 給定n,如何求出(a+b)^n所有項的係數呢? 方法一,遞推,利用楊輝三角的性質,當前數等於上方兩個數的和,表現在組合數上就是C(n,m)=C(n,m-1)+C(n-1,m-1)。 程式碼如下:

另一方面,將(a+b)^n展開,係數正好和楊輝三角一致。 一般有(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)b+...+C(n,n)b^n。 給定n,如何求出(a+b)^n所有項的係數呢? 方法一,遞推,利用楊輝三角的性質,當前數等於上方兩個數的和,表現在組合數上就是C(n,m)=C(n,m-1)+C(n-1,m-1)。 程式碼如下:
但是複雜度是n^2。 方法二,利用等式C(n,k)=(n-k+1)/k*C(n,k-1)。從C(n,0)=1開始遞推。 程式碼:memset(C,0,sizeof(C)); for (int i = 0; i <= n; ++i) { C[i][0] = 1; for (int j = 1; j <= i; ++j) { C[i][j] = C[i][j - 1] + C[i - 1][j - 1]; } }
C[0] = 1;
for (int i = 1; i <= n; ++i) {
C[i] = (n-i+1)*C[i-1]/i;
}