變態組合數C(n,m)求解
（在求卡特蘭數時有 一定作用）
問題：求解組合數C(n,m)，即從n個相同物品中取出m個的方案數，由於結果可能非常大，對結果模10007即可。
方案一 暴力求解，C(n,m)=n*(n-1)*...*(n-m+1)/m! int Combination(int n, int m) { const int M = 10007; int ans = 1; for(int i=n; i>=(n-m+1); --i) ans *= i; while(m) ans /= m--; return ans % M; } 這種方案的缺陷是，在計算過程中很快ans就溢位了，一般情況下，n不能超過12。補救辦法之一是將先乘後除改為交叉地進行乘除，先除能整除的，但也只能滿足n稍微增大的情況，n最多隻能滿足兩位數。補救辦法之二是換用高精度運算，這樣結果不會有問題，只是需要實現大數相乘、相除和取模等運算，實現起來比較麻煩，時間複雜度為O(n)。 方案二
滿足下式：
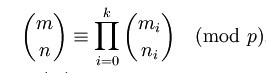即C(n,m)模p等於p進位制數上各位的C(ni,mi)模p的乘積。利用該定理，可以將計算較大的C(n,m)轉化成計算各個較小的C(ni,mi)。
該方案能支援整型範圍內所有數的組合數計算，甚至支援64位整數，注意中途溢位處理。該演算法的時間複雜度跟n幾乎不相關了，可以認為演算法複雜度在常數和對數之間。
#include <stdio.h>
const int M = 10007;
int ff[M+5]; //打表，記錄n!，避免重複計算
//求最大公因數
int gcd(int a,int b)
{
if(b==0)
return a;
else
return gcd(b,a%b);
}
//解線性同餘方程，擴充套件歐幾里德定理
int x,y;
void Extended_gcd(int a,int b)
{
if(b==0)
{
x=1;
y=0;
}
else
{
Extended_gcd(b,a%b);
long t=x;
x=y;
y=t-(a/b)*y;
}
}
//計算不大的C(n,m)
int C(int a,int b)
{
if(b>a)
return 0;
b=(ff[a-b]*ff[b])%M;
a=ff[a];
int c=gcd(a,b);
a/=c;
b/=c;
Extended_gcd(b,M);
x=(x+M)%M;
x=(x*a)%M;
return x;
}
//Lucas定理
int Combination(int n, int m)
{
int ans=1;
int a,b;
while(m||n)
{
a=n%M;
b=m%M;
n/=M;
m/=M;
ans=(ans*C(a,b))%M;
}
return ans;
}
int main(void)
{
int i,m,n;
ff[0]=1;
for(i=1;i<=M;i++) //預計算n!
ff[i]=(ff[i-1]*i)%M;
scanf("%d%d",&n, &m);
printf("%d\n",func(n,m));
return 0;
}
方案五：
一個比較有用且是在O（n）時間內實現公式：C(n,r)=(n-r+1)/r*C(n,r-1);
由C(n,0)直接往上推即可；
方案六：（一般這種方法在計算機上不能對大數進行實現）
計算組合數最大的困難在於資料的溢位，對於大於150的整數n求階乘很容易超出double型別的範圍，那麼當C(n,m)中的n=200時，直接用組合公式計算基本就無望了。另外一個難點就是效率。
對於第一個資料溢位的問題，可以這樣解決。因為組合數公式為：
C(n,m) = n!/(m!(n-m)!)
為了避免直接計算n的階乘，對公式兩邊取對數，於是得到：
ln(C(n,m)) = ln(n!)-ln(m!)-ln((n-m)!)
進一步化簡得到：
這樣我們就把連乘轉換為了連加，因為ln(n)總是很小的，所以上式很難出現資料溢位。
為了解決第二個效率的問題，我們對上式再做一步化簡。上式已經把連乘法變成了求和的線性運算，也就是說，上式已經極大地簡化了計算的複雜度，但是還可以進一步優化。從上式中，我們很容易看出右邊的3項必然存在重複的部分。現在我們把右邊第一項拆成兩部分：
這樣，上式右邊第一項就可以被抵消掉，於是得到：
上式直接減少了2m次對數計算及求和運算。但是這個公式還可以優化。對於上面公式裡的求和，當m<n/2時，n-m是一個很大的數，但是當m>n/2時，n-m就會小很多。我們知道：
C(n,m) = C(n,n-m)
那麼通過這個公式，我們可以把小於n/2的m變為大於n/2的n-m再進行計算，結果是一樣的，但是卻能減少計算量。
當計算出ln(C(n,m))後，只需要取自然對數，就可以得到組合數：
C(n,m) = exp(ln(C(n,m)))
這樣就完成了組合數的計算。
用這種方法計算組合數，如果只計算ln(C(n,m))的話，n可以取到整型資料的極限值65535，
ln(C(65535,32767)) = 45419.6
而計算時間只需要0.01ms。當然，如果要取對數得到最終的組合數的話，n的取值就不能達到這麼大了。但是這種演算法仍然可以保證n取到1000以上，而不是開頭說的150這個極限值。例如:
C(1000,500) = 2.70288e+299
計算時間仍然小於0.01ms。
採用我這種演算法，不僅n的取值範圍大，而且計算速度高，不像用遞迴演算法實現這個問題的時候，很容易陷入遞迴層次太深而導致計算時間太長。
演算法程式碼實現如下：
1 double lnchoose(int n, int m)
2 {
3 if (m > n)
4 {
5 return 0;
6 }
7 if (m < n/2.0)
8 {
9 m = n-m;
10 }
11 double s1 = 0;
12 for (int i=m+1; i<=n; i++)
13 {
14 s1 += log((double)i);
15 }
16 double s2 = 0;
17 int ub = n-m;
18 for (int i=2; i<=ub; i++)
19 {
20 s2 += log((double)i);
21 }
22 return s1-s2;
23 }
24
25 double choose(int n, int m)
26 {
27 if (m > n)
28 {
29 return 0;
30 }
31 return exp(lnchoose(n, m));
32 }