博弈基礎——極大極小搜尋
阿新 • • 發佈：2018-12-25
計算機博弈（也稱機器博弈），是一個挑戰無窮、生機勃勃的研究領域，是人工智慧領域的重要研究方向，是機器智慧、兵棋推演、智慧決策系統等人工智慧領域的重要科研基礎。機器博弈被認為是人工智慧領域最具挑戰性的研究方向之一。
機器博弈的核心技術是博弈搜尋演算法
零和博弈（zero-sum game），又稱零和遊戲，與非零和博弈相對，是博弈論的一個概念，屬非合作博弈。指參與博弈的各方，在嚴格競爭下，一方的收益必然意味著另一方的損失，博弈各方的收益和損失相加總和永遠為“零”，雙方不存在合作的可能。
也可以說：自己的幸福是建立在他人的痛苦之上的，二者的大小完全相等，因而雙方都想盡一切辦法以實現“損人利己”。零和博弈的結果是一方吃掉另一方，一方的所得正是另一方的所失，整個社會的利益並不會因此而增加一分。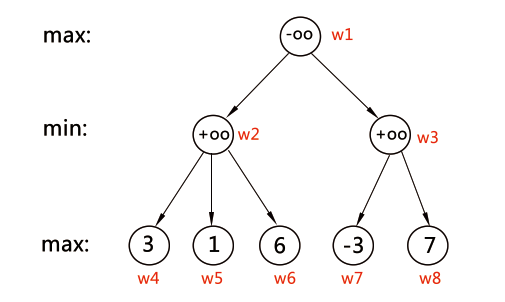 
假如有如上圖的博弈樹，設先手為 A ，後手為 B ；則 A 為 max 局面，B 為 min 局面。上圖中 A 一開始有 2 種走法（ w2 和 w3 ，w表示結點記號），它走 w2 還是 w3 取決於 w2 和 w3 的估價函式值f()，因為 A 是 max 局面，所以它會取 f(w2) 和 f(w3) 中大的那個，f(x) 怎麼求呢？通常是以遞迴的方式對博弈樹進行搜尋，我們通常可以設定葉子結點局面的估價值。
但是，實際問題中的所有局面所產生的博弈樹一般都是非常龐大，非常龐大的多叉樹~，並不能依靠暴力搜尋來尋找最佳解法。因此需要用到一些剪枝手段。常用的比較初級的有 alpha-beta 剪枝。 簡單地說就是用兩個引數 alpha 和 beta 表示當前局面的父局面的估價函式值 f()。如果當前局面為 min 局面，則需要藉助父局面目前已求得的 f() （即 alpha）來判斷是否需要繼續搜尋下去；如果當前局面為 max 局面，則需要藉助父局面目前已求得的 f() （即 beta）。 具體來說就是這樣，舉個例子： 如果下圖是某問題所產生的一顆博弈樹，先手 A 為己方，後手 B 為對方。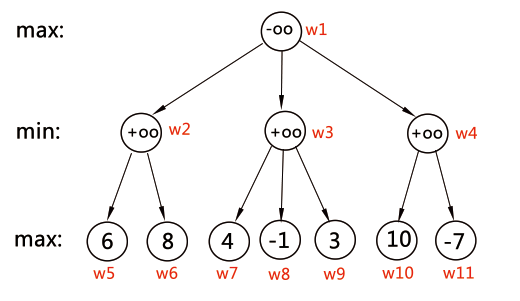
通過前面所述的方法，如果 A 走 w2 則可以得到這樣的結果：
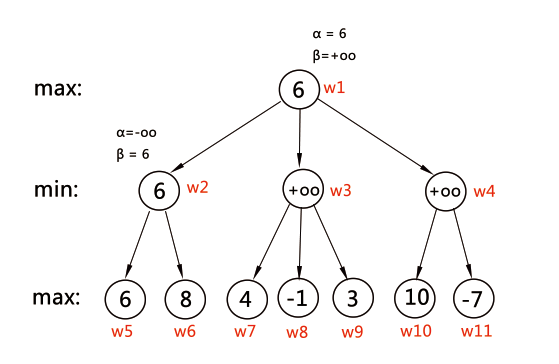
alpha 初始值為 -oo，beta 初始值為 +oo；w1 在得到 f(w1) = 6 的整個過程中， alpha 和 beta 是這樣變化的：w1 --> w2 -- > w5 得到 f'(w2) = 6 < f(w2) = +oo，即修改 f(w2) = f'(w2) = 6；同時修改 beta = 6 (因為 w2 的子局面是否需要剪枝依賴於 w2 的估價值 f()，而與 alpha 無關，故不需修改 alpha)。在正常搜尋完 w1 --> w2 --> w6 後， w2 層把 beta = 6 返回給上一層 w1 的 alpha，即 w1 層的 alpha = 6，beta = +oo。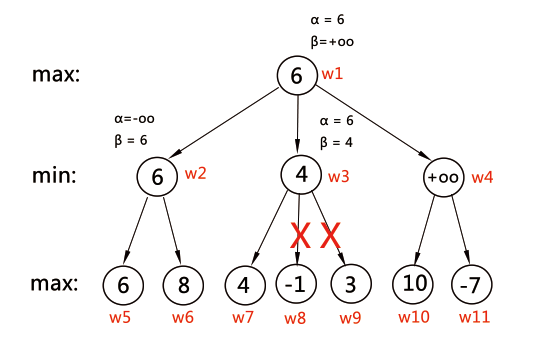
接下來在 w3 裡搜尋就可以體現 alpha-beta 剪枝的效果；A 在選擇 w3 走的時候同時把所得的 alpha 和 beta 傳遞下去，在經過 w1 --> w3 --> w7 得到 f(w3) = 4 (同時使 beta = 4)後，首先進行判斷：如果 alpha > beta，則直接返回 beta = 4，沒有必要再搜尋 w8 和 w9。這是因為這個 alpha 是 w1 在走 w2 這條路時得到的一個估價值 f(w1)，而 w3 是 min 局面，它會選擇子局面 w7, w8, w9 中 f() 的值小的作為 f(w3)，所以 w3 在得到 f(w3) = 4 後如果繼續搜尋 w8, w9，只會得到更小的值；w1 是 max 局面，它的 f() 要修改的條件是找到估價值比它更大的子局面，而 w1 目前已知的估價值 f(w1) = 6 比 f(w3) 要大，所以無論 w3 再怎麼繼續搜尋下去，w1 都不會選 w3 作為下一步，所以沒有必要搜尋下去。這樣就剪掉了 w8, w9 這兩個分支，直接跳出 w3 進入 w4 繼續搜尋。另外一種情形也是類似的道理，這樣就實現了有效的剪枝優化。 偽程式碼表示為：
練習：
假如有如上圖的博弈樹，設先手為 A ，後手為 B ；則 A 為 max 局面，B 為 min 局面。上圖中 A 一開始有 2 種走法（ w2 和 w3 ，w表示結點記號），它走 w2 還是 w3 取決於 w2 和 w3 的估價函式值f()，因為 A 是 max 局面，所以它會取 f(w2) 和 f(w3) 中大的那個，f(x) 怎麼求呢？通常是以遞迴的方式對博弈樹進行搜尋，我們通常可以設定葉子結點局面的估價值。
// player = 1 表示輪到己方， player = 0 表示輪到對方
// cur_node 表示當前局面(結點)
maxmin(player, cur_node)
{
if 達到終結局面
return 該局面結點的估價值 f
end
if player == 1 // 輪到己方走
best = -oo // 己方估價值初始化為 -oo
for 每一種走法 do
new_node = get_next(cur_node) // 遍歷當前局面 cur_node 的所有子局面
val = maxmin(player^1, new_node); // 把新產生的局面交給對方，對方返回一個該局面的估價值
if val > best
best = val;
end
end
return best;
else // 輪到對方走
best = +oo // 對方估價值初始化為 +oo
for 每一種走法 do
new_node = get_next(cur_node) // 遍歷當前局面 cur_node 的所有子局面
val = maxmin(player^1, new_node); // 把新產生的局面交給對方，對方返回一個該局面的估價值
if val < best
best = val;
end
end
return best;
end
}但是，實際問題中的所有局面所產生的博弈樹一般都是非常龐大，非常龐大的多叉樹~，並不能依靠暴力搜尋來尋找最佳解法。因此需要用到一些剪枝手段。常用的比較初級的有 alpha-beta 剪枝。 簡單地說就是用兩個引數 alpha 和 beta 表示當前局面的父局面的估價函式值 f()。如果當前局面為 min 局面，則需要藉助父局面目前已求得的 f() （即 alpha）來判斷是否需要繼續搜尋下去；如果當前局面為 max 局面，則需要藉助父局面目前已求得的 f() （即 beta）。 具體來說就是這樣，舉個例子： 如果下圖是某問題所產生的一顆博弈樹，先手 A 為己方，後手 B 為對方。
通過前面所述的方法，如果 A 走 w2 則可以得到這樣的結果：
alpha 初始值為 -oo，beta 初始值為 +oo；w1 在得到 f(w1) = 6 的整個過程中， alpha 和 beta 是這樣變化的：w1 --> w2 -- > w5 得到 f'(w2) = 6 < f(w2) = +oo，即修改 f(w2) = f'(w2) = 6；同時修改 beta = 6 (因為 w2 的子局面是否需要剪枝依賴於 w2 的估價值 f()，而與 alpha 無關，故不需修改 alpha)。在正常搜尋完 w1 --> w2 --> w6 後， w2 層把 beta = 6 返回給上一層 w1 的 alpha，即 w1 層的 alpha = 6，beta = +oo。
接下來在 w3 裡搜尋就可以體現 alpha-beta 剪枝的效果；A 在選擇 w3 走的時候同時把所得的 alpha 和 beta 傳遞下去，在經過 w1 --> w3 --> w7 得到 f(w3) = 4 (同時使 beta = 4)後，首先進行判斷：如果 alpha > beta，則直接返回 beta = 4，沒有必要再搜尋 w8 和 w9。這是因為這個 alpha 是 w1 在走 w2 這條路時得到的一個估價值 f(w1)，而 w3 是 min 局面，它會選擇子局面 w7, w8, w9 中 f() 的值小的作為 f(w3)，所以 w3 在得到 f(w3) = 4 後如果繼續搜尋 w8, w9，只會得到更小的值；w1 是 max 局面，它的 f() 要修改的條件是找到估價值比它更大的子局面，而 w1 目前已知的估價值 f(w1) = 6 比 f(w3) 要大，所以無論 w3 再怎麼繼續搜尋下去，w1 都不會選 w3 作為下一步，所以沒有必要搜尋下去。這樣就剪掉了 w8, w9 這兩個分支，直接跳出 w3 進入 w4 繼續搜尋。另外一種情形也是類似的道理，這樣就實現了有效的剪枝優化。 偽程式碼表示為：
// player = 1 表示輪到己方， player = 0 表示輪到對方
// cur_node 表示當前局面(結點)
maxmin(player, cur_node, alpha, beta)
{
if 達到終結局面
return 該局面結點的估價值 f
end
if player == 1 // 輪到己方走
for 每一種走法 do
new_node = get_next(cur_node) // 遍歷當前局面 cur_node 的所有子局面
val = maxmin(player^1, new_node, alpha, beta); // 把新產生的局面交給對方，對方返回一個新局面的估價值
if val > alpha
alpha = val;
end
if alpha > beta
return alpha;
end
end
return alpha;
else // 輪到對方走
for 每一種走法 do
new_node = get_next(cur_node) // 遍歷當前局面 cur_node 的所有子局面
val = maxmin(player^1, new_node, alpha, beta); // 把新產生的局面交給對方，對方返回一個新局面的估價值
if val < beta
beta = val;
end
if alpha > beta
return beta;
end
end
return beta;
end
}
練習：