Unique Paths(不同的路徑總數)

【難度：Medium】
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

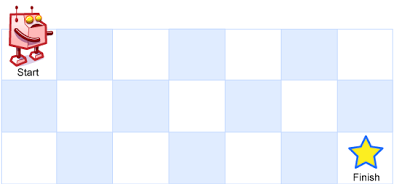
位於m*n矩陣的一個機器人只能向下或向右移動，求其從Start移動到Finish不同的走法總數。

解題思路

這是一道典型的動態規劃問題，使用一個二維陣列ans記憶到達每一點可行的走法總數。首先將左邊界點和上邊界點初始化為1，因為機器人起始與（0，0），左邊界點和上邊界點的走法只有1種。接下來的每一點（x,y），可以由（x-1，y）向右走或是（x,y-1）向下走來到達，因此在（x,y）這一點可到達的方法有ans[x-1][y]+ans[x][y-1]種，到達終點的方法則是ans最後一個點的資料。

c++程式碼如下

class Solution {
public:
    int uniquePaths(int m, int n) {
        if (m == 0 || n == 0) {
            return 0;
        }
        vector<vector<int>> path(m,vector<int>(n,0));
        for (int i = 0; i < m; i++)
            path[i][0] = 1;
        for (int i = 0; i < n; i++)
            path[0
 
][i] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                path[i][j] = path[i-1][j] + path[i][j-1];
            }
        }
        return path[m-1][n-1];
    }
};