參考論文：
《基於標籤傳播的社群挖掘演算法研究綜述》王庚等

參考部落格：
https://www.cnblogs.com/end/p/6364345.html

基礎概述

開始瞭解社群發現的時候，我以為這只是一種演算法。後來深入下去才知道，它的狀態是，上有老下有小的情況。
向上走：社群發現 $\in$ 複雜網路聚類 $\in$

\in 圖論
由於項上走實在知識面太廣，有待後期學習。所以決定先往下走。
向下走：各種相關演算法 如LPA、BMLPA、LPAm、LPAm+、Fast Unfolding……
雖然社群發現演算法的孩子也很多，但是它們兄弟之間都是有相關性的。各有優劣。下面我將首先對社群發現的相關概念做出論述後，再一一介紹社群發現演算法的孩子們的故事。

社群：我們認為一張圖中連線緊密的一組點構成的集合為一個社群。而社群與社群之間的連線是非常稀疏的。
社群發現：顧名思義，就是在關係圖中找社群的過程。需要注意的是，社群發現是一種半監督學習

。
隨機圖：一個圖中任何兩點之間邊的概率相等。首先，確定n個點，然後以固定概率去給圖中一對頂點連邊，形成隨機圖 (這個過程可以用過鄰接矩陣完成)

那麼隨機圖跟我們的社群發現有什麼關係呢？其實它就是一個參照。我們可以這樣認為，隨機圖就是一張底線圖，因為隨機圖中各節點的連線都是隨機的，且每兩個節點的連線概率都是相等的，因此認為隨機圖中基本沒有所謂社群可言。因此認為與隨機圖相差越大，社群結構約明顯。那麼如何來衡量區別大小呢，就是用Modularity係數 (Newman 和 Girvan於2004年提出的)。

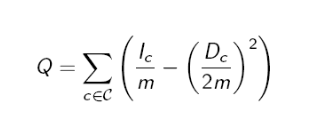
m,圖中總邊數；
$l_{}$

c l_{c} ：社群c中所有內部邊的條數
$D_{c}$：社群c中所有定點的度之和
公式理解：首先，計算每個社群，內部邊的條數佔圖中總條數的比例與社群中總度數佔圖中總度數的比例之差。然後計算所有劃分出的社群的這個值。
問題思考：根據概念，modularity 是與隨機圖有緊密關係的，怎麼體現出與隨機圖的緊密關係。
個人理解：如果是隨機圖情況，相較於社群結構較明顯的圖， $l_{c}/m$較小，而 $D_{c}/2m$較大，整體也就較小。所以Q越大，圖的社群結構越明顯。

開始我們的演算法之旅吧

社群發現的演算法分類方式：非同步演算法和同步演算法、重疊演算法和非重疊演算法
同步演算法：是指一次更新全部節點，本次每個節點標籤的更新結果只與之前的結果有關，與本次更新結果無關。
非同步演算法:是指本次對每個節點的更新不僅與之前的結果有關，還與本次已更新完的結果有關。假設節點 i 要依賴節點j進行更新，但節點 j 在本輪迭代中已經更新為了 j’ ，那麼在非同步演算法中，將使用 j’ 來更新節點 i 。
實驗研究表明，非同步更新策略相對同步更新來說可能需要更多的迭代次數，但是得到的社群結構也相對更加穩定。
非重疊演算法：每個節點標籤是唯一的。
重疊演算法：每個節點標籤是不唯一的。
好了，下面開始來我們的經典演算法吧。下面是我們的演算法講述流程圖。

LPA演算法

LPA演算法是2002年由zhu等提出的，在2007年被Usha、Nandini、Raghavan應用到了社群發現領域，提出了RAK演算法。但是大部分研究者稱RAK演算法為LPA演算法。
演算法思想：

1. 為所有節點指定一個唯一標籤
2. 逐輪重新整理所有節點的標籤，直到達到收斂要求為止。

重新整理規則：
以鄰域中出現最多的那一類為中心點label。
缺點：可能出現所有頂點被劃分到一個巨大社群的情況。為了防止這種情況發生，LPAm演算法被提出。

LPAm演算法

LPAm演算法，即模組化標籤傳播演算法。2009年由Lan X.Y提出。主要有Hop Attenuation(跳躍衰減)和Node Preference（節點傾向性選擇）兩部分組成。

• Hop Attenuation
  

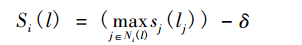
式中， $s( l)$ 表示的是節點 i 上標籤 l 的評分; $l_{j}$表示的是節點 j 的標籤; $N( l)$ 表示的是節點 i 的鄰接點中標籤為 $l$ 的節點集合; $δ$ 為衰減因子。初始化時節點的評分為 1，隨著標籤傳播的過程評分會逐漸地減小，當評分降低為 0 的時候， 這個標籤就無法再傳遞給其他節點，通過引入跳躍衰減的策略就能有效地避免大社群的形成。

• Node Preference
  通過後續的研究， 實驗結果發現跳躍衰減結合節點傾向性選擇將能取得更好的效果， 在這兩種策略結合的情況下，節點 i 的新標籤 $l^{'}_{i}$ 為:
  

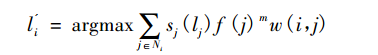
其中， $w( i，j)$ 表示節點 i 和節點 j 之間邊的權重; $f( j)$ 表示的是節點傾向性選擇函式; m 引數起到一個平衡因子的作用。Barber 等人在實驗中初始 $f( j) = 1$， 即表示節點的度數為 1。這樣的話， 如果取 $m ＞ 0$， 就表示演算法傾向於選擇鄰接點中度數較大的節點所帶有的標籤，若一開始取 m ＜ 0 則表示相反的選擇。在通常情況下，m 取 0.1。
缺點：可能會存在陷入區域性極大值情況。為了防止這種情況提出了LPAm+演算法。

LPAm+

LPAm+ 演算法實際上就是LPAm演算法與MSG演算法合併。
方法：通過MSG演算法，可有效合併多個相似社群。具體方法可以查閱資料，或等待後期更新。

COPRA演算法和BMLPA演算法

COPRA演算法，是一種重疊演算法。BMLPA 演算法（Balanced Multi-Label Propagation Algorithm），由北京交通大學武志昊於2012年提出的。它是一種重疊挖掘演算法，是對COPRA演算法的改進。

COPRA演算法：
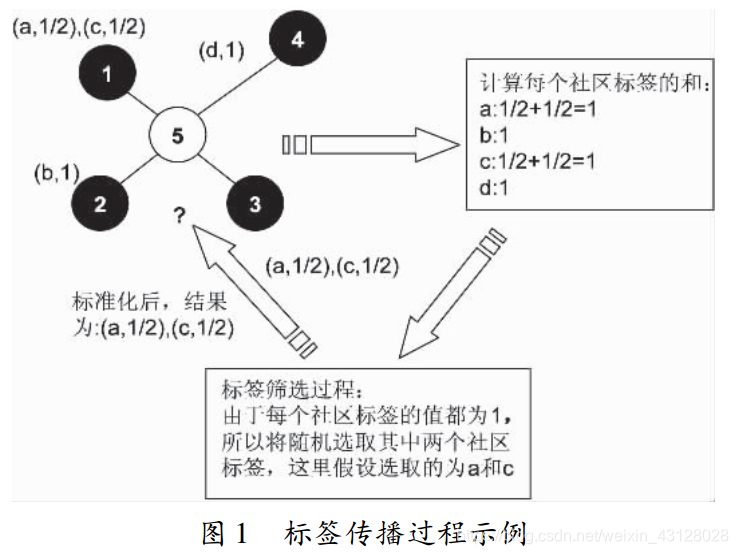
社群標籤計算（c,b）。

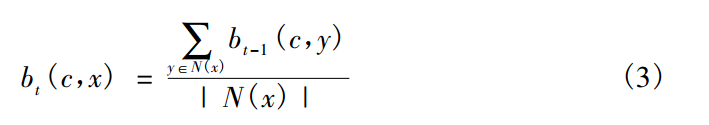
首先要計算其鄰接點中所存在的社群標籤的和， 接下來選擇 v個數值最大的標籤( v 表示設定的重疊社群個數， 圖中v 的值為 2) 。若存在多個可選標籤的話， 這時就需要進行標籤的隨機選擇， 最後再將所選的標籤進行標準化得到節點 5 的標籤更新結果。

BMLPA的條件是不再侷限於v個，而是通過更改閾值p來限制標籤數。

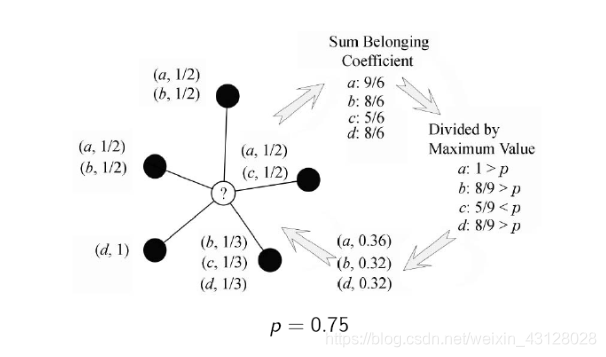
優缺點：
COPRA演算法,在遇到存在多個標籤可選的情況下，該演算法會隨機進行選擇，在這個過程中會導致該演算法不穩定性。
BMLPA演算法，不再需要初始化v的值，也就是說挖掘的重疊社群數目不再受引數v的限制。這樣做雖然增加了演算法的穩定性，但隨之帶來的是該演算法挖掘得到的社群結構比較固定，使得演算法的適應性有所下降。