A、B兩個矩陣均是nxn的矩陣，則兩個矩陣的乘法：

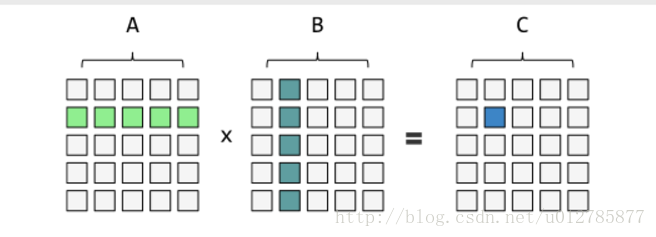
一般的矩陣乘法程式碼：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <unistd.h>
#include <time.h>

class SquareMatrix {
public:
    SquareMatrix(){}
    SquareMatrix( int row, int col ):
        mRow(row), mCol(col)
    {
        Init();
    }
    ~SquareMatrix()
    {
        for ( int i = 0; i < mRow; i++ ) {
            delete[] mElement[i];
            //printf("delete %d\n", i);
        }
        delete[] mElement;
    }
    void Init()
    {
        mElement = new int*[mRow];
        for ( int i = 0; i < mCol; i++ ) {
            mElement[i] = new int[i];
        }
    }
    void SetElement( int lowV, int upV )
    {
        int size = upV - lowV;

        for ( int i = 0; i < mRow; i++ ) {
            for ( int j = 0; j < mCol; j++ ) {
                mElement[i][j] = rand() % size + lowV;
            }
        }
    }
    void PrintElement()
    {
        printf("=========================================\n");
        for ( int i = 0; i < mRow; i++ ) {
            for ( int j = 0; j < mCol; j++ ) {
                printf("%d ", mElement[i][j]);
            }
            printf("\n");
        }
        printf("=========================================\n");
    }
public:
    int mRow;
    int mCol;
    int *(*mElement);
};
void SquareMatrixMultiply( 
    SquareMatrix &a, 
    SquareMatrix &b, 
    SquareMatrix &c )
{
    int n = a.mRow;

    c.mRow = c.mCol = n;
    c.Init();

    for ( int i = 0; i < n; i++ ) {
        for ( int j = 0; j < n; j++ ) {
            c.mElement[i][j] = 0;
            for ( int k = 0; k < n; k++ ) {
                c.mElement[i][j] += a.mElement[i][k] * b.mElement[j][k];
            }
        }
    }
}
int main( int argc, char **argv ) 
{

    if ( argc != 2 ) {
        printf("Usage:./binaryfile num\n");
        exit( 0 );
    }

    int n = atoi( argv[1] );

    SquareMatrix smA( n, n ), smB( n, n ), smC;
    smA.SetElement( 1, 10 );
    smA.PrintElement();

    smB.SetElement( 1, 10 );
    smB.PrintElement();

    SquareMatrixMultiply( smA, smB, smC );
    smC.PrintElement();

    printf("init square matrix finished\n");
    return 0;
}
 

演算法複雜度為O(n^3)，而Stranssen演算法通過分治法將大矩陣切分為小矩陣進行計算，演算法複雜度可以降低為O(n^2.81)，但是嘗試寫下程式碼，發現切割子矩陣時有點複雜，普通的切分會建立子矩陣並複製值，而用下標進行計算又比較複雜，下次有空再嘗試寫吧。