邏輯迴歸(Logistic Regression)分類器
阿新 • • 發佈:2018-12-14
目錄
吃了概率論的虧
邏輯迴歸(Logistic Regression)概述
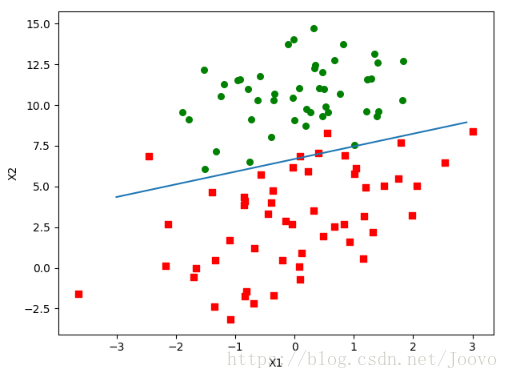
直觀來說,用一條直線對一些現有的資料點進行擬合的過程,就叫做迴歸。Logistic分類的主要思想:根據現有資料對分類邊界建立迴歸公式,並以此分類。建立擬合引數的過程中用到最優化演算法,這裡用到的是常用的梯度上升法。
一個直觀的圖片:
一般過程 (1) 收集資料:採用任意方法收集資料。 (2) 準備資料:由於需要進行距離計算,因此要求資料型別為數值型。另外,結構化資料 格式則最佳。 (3) 分析資料:採用任意方法對資料進行分析。 (4) 訓練演算法:大部分時間將用於訓練,訓練的目的是為了找到最佳的分類迴歸係數。 (5) 測試演算法:一旦訓練步驟完成,分類將會很快。 (6) 使用演算法:首先,我們需要輸入一些資料,並將其轉換成對應的結構化數值; 接著,基於訓練好的迴歸係數就可以對這些數值進行簡單的迴歸計算,判定它們屬於 哪個類別;在這之後,我們就可以在輸出的類別上做一些其他分析工作。
Logistic迴歸分類器,Sigmoid 函式
Logistic迴歸
優點:計算代價不高,易於理解和實現。
缺點:容易欠擬合,分類精度可能不高。
適用資料型別:數值型和標稱型資料。
我們想要一個函式,接受所有輸入並返回我們的預測值,sigmoid函式符合我們的要求。
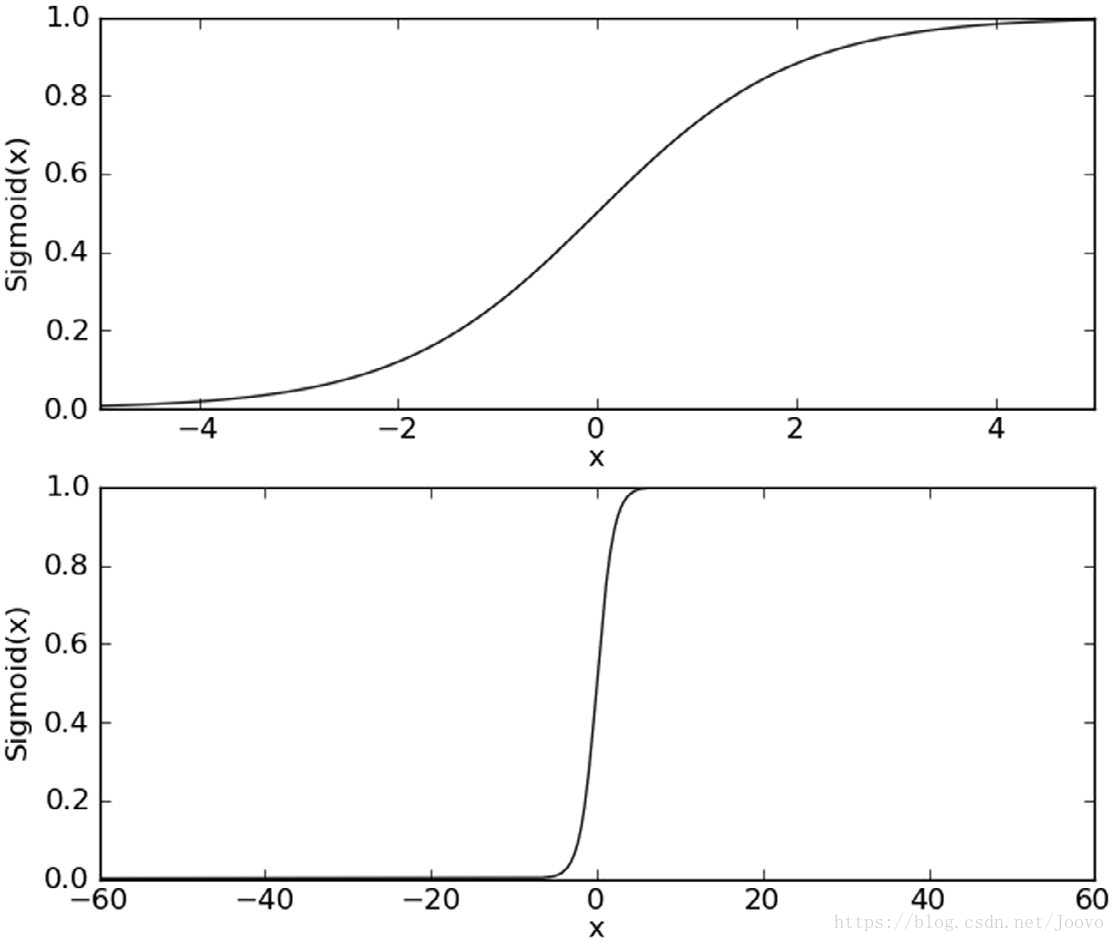
x
x乘上一個迴歸係數w,再求和,sum作為自變數代入sigmoid函式,就得到一個0-1範圍內的數了。接下來確定迴歸係數(weight)。
性質:
最優化理論確定迴歸係數(weight/θ)
迴歸係數即weight/θ,我們初始化迴歸係數為1,再不停用梯度上升法迭代,優化這個係數,直到最大迭代次數或是w達到誤差範圍內。
sigmoid的輸入記為z,那麼
所以sigmoid也可以寫為
梯度上升法
要找到某個函式的最大值,最好最快的方法就是沿著函式的梯度方向探尋。如果梯度記為▽(讀作“Nabla”),那麼函式f(x,y)的梯度由下式表示:
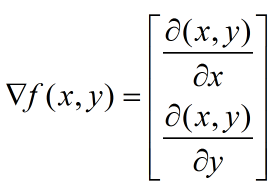
數學推導
定義 y 為根據g(z)來判斷類別的結果,為1或0。 首先 g(z) 就是它等於1的概率,即概率密度函式,那麼根據上述定義: 概率函式為 似然函式,聯合概率密度函式: 即 取對數似然函式: 其梯度運算元: 代入,求導:
所以:
畫出決策邊界
z=0時,g(z)=0.5 是兩個類別的分界。因此令 即為擬合直線的方程。
from numpy import *
import matplotlib.pyplot as plt
def sigmoid(inX):
return 1.0 / (1 + exp(-inX))
def load_dataset():
data_mat = []
label_mat = []
with open('testSet.txt', 'r')as file:
for line in file.readlines():
cur_line = line.strip().split()
data_mat.append([1.0, float(cur_line[0]), float(cur_line[1])])
label_mat.append(float(cur_line[-1]))
return data_mat, label_mat
# gradient ascent 梯度 上升
def grad_ascent(data_mat, label_mat):
data_mat = mat(data_mat) # convert to np matrix
label_mat = mat(label_mat).transpose()
m, n = shape(data_mat)
weights = ones((n, 1)) # init the weight
alpha = 0.001
max_cycles = 500
for k in range(max_cycles):
h = sigmoid(data_mat * weights) # m*1
error = (label_mat - h)
weights += alpha * data_mat.transpose() * error
return weights
def plot_best_fit(data_mat, label_mat, weights):
# 畫所有點,用綠色紅色標出
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
n = shape(data_mat