一、對映

設X，Y是兩個非空集合，如果存在一個法則f

·使得對x中每個元素x 按法則f

·在Y中有唯一確定的元素y與之對應，

·則稱f為從X到Y的對映 記作f:X->Y

·元素y稱為元素x的像，元素x稱為元素y的一個原像

舉例:照鏡子 鏡子中也有一個你 (像和原像

·定義域:集合X稱為對映f的定義域 記作Df 即Df=X

·值域:X中所有元素的像組成的集合稱為對映f的值域

     記作Rf或f(X) 即:

          Rf = f(X) = {f(x)|x∈X}

對映三要素

·集合X 即定義域Df=X

·集合Y 即值域的範圍 Rf⊂Y  （Y不是值域，Y包含Rf）

·對應法則f 使對每個x∈X 有唯一確定的y=f(x)與之對應

注意

·對每個x∈X 元素x的像y是唯一的

·對每個y∈Rf 元素y的原像不一定是唯一的

·對映f的值域Rf是Y的一個字集 即Rf⊂Y 不一定Rf=Y

·滿射 Rf=Y

·單射 任意x1 x2 ∈X x1≠x2 有f(x1)≠f(x2)
·一一對映:滿射+單射

·函式的概念

函式的定義(function)

·設數集D⊂R(實數集) 則稱對映f:D->R為定義在D上的函式 通常簡記為y=f(x) x∈D

·其中x稱為自變數，y稱為因變數 D稱為定義域 記作Df 即Df=D

·函式值:對每個x∈D 按對應法則f 總有唯一確定的值y與之對應 這個值稱為函式f在x處的函式值 記作f(x)

·函式關係:因變數y與自變數x之間的這種依賴關係稱為函式關係

·值域:函式值f(x)全體構成的集合稱為函式f的值域 記作Rf或f(D)

函式的兩要素

·定義域與對應法則

函式的定義域

·有實際意義背景的函式 根據實際背景中變數的實際意義確定

例:自由落體運動 s= 1/gt^2 t∈[0,T]

·抽象的用算式表達的函式 其定義域是自變數所能取的使算式有意義的一切實數值

y= D:[-1,1]

y= （分母不能為0 根號內也要大於0 所以使(-1,1)

函式的圖形表示方法

·座標平面上的點集{P(x,y)|y=f(x),x∈D},稱為函式y=f(x) x∈D的圖形

特殊函式舉例:

·符號函式

·y=sgnx = {1(當x>0    0(當x=0       -1(當x<0

（想象一下它的圖形）

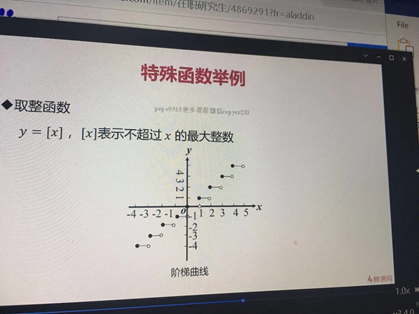
·取整函式

y=[x],[x]表示不超過x的最大整數

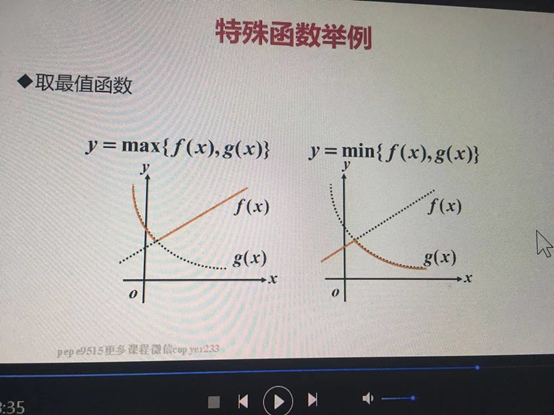
·取最值函式

y=max{f(x),g(x)}

·分段函式

·在自變數的不同變化範圍中，對應法則用不同的式子來表示的函式，稱為分段函式

三、函式的特性

函式的有界性

·若X⊂D 存在M>0 對任意x∈X 有|f(x)|<=M成立 則成f(x)在X上有界，否則稱無界

函式的單調增加性

·設函式f(x)的定義域為D 區間I⊂D

·如果對於區間I上任意兩點x1及x2

·當x1<x2 恆有f(x1)<f(x2)

則稱f(x)在區間I上是單調增加的

函式的單調減少性

…

函式的奇偶性

·設D關於原點對稱

·對於任意x∈D 有f(-x)=f(x)

則稱函式f(x)為偶函式

·設D關於原點對稱，

·對於任意x∈D 有f(-x)=-f(x)

則稱函式f(x)為奇函式

函式的週期性

·設函式f(x)的定義域為D 如果存在一個不為零的數l 使得對於任一x∈D (x+-l)∈D 且f(x+l)=f(x)恆成立，則稱f(x)為周期函式,l稱為f(x)的函式

四、初等函式

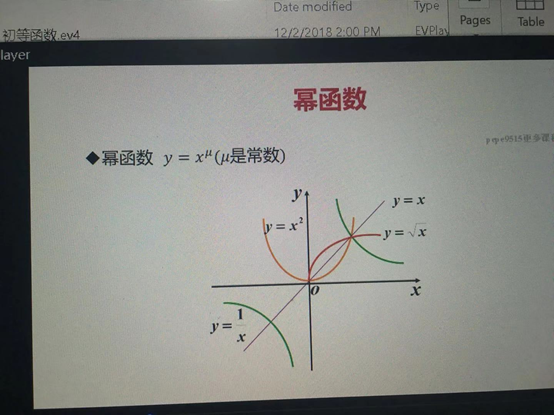
·冪函式 y=x^u

·指數函式 y=a^x

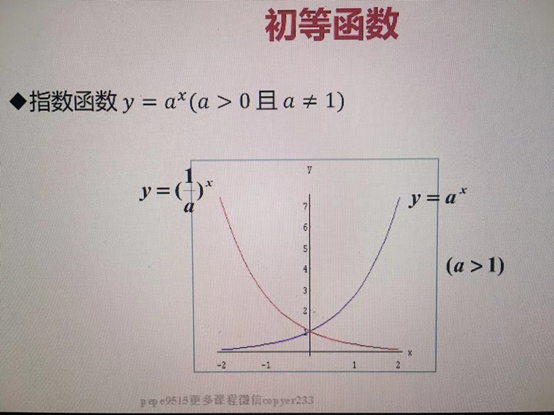
·對數函式 y = logax (a>0且a≠1)

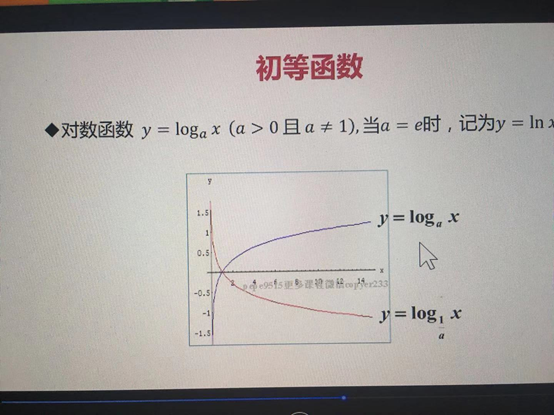
1) 當a=e時 記為y=lnx

·三角函式

  ·正弦函式 y = sinx

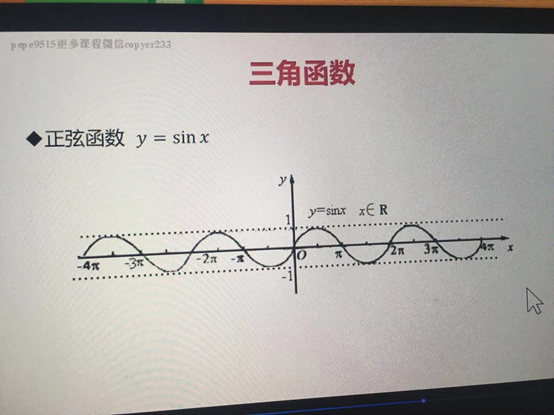
  ·餘弦函式 y = cosx

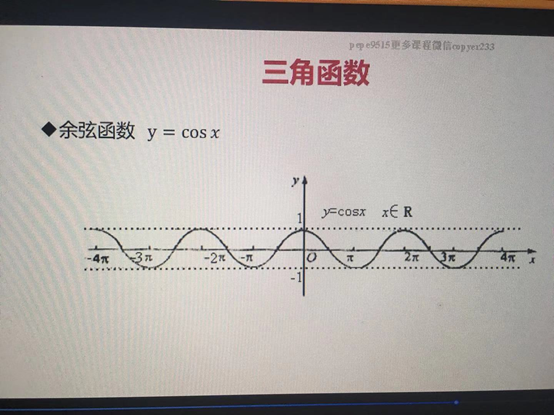
  ·正切函式 y = tanx

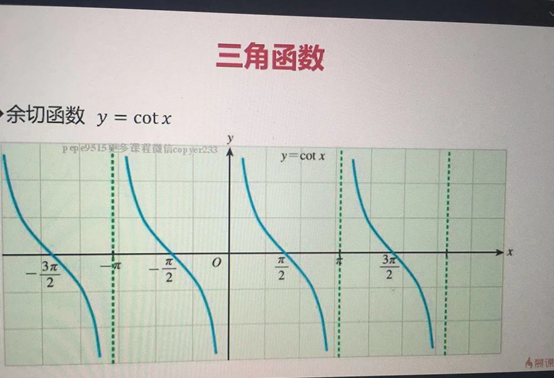
  ·餘切函式 y = cotx