高等數學(4) 數列與數列極限
一、數列與數列極限
劉徽——割圓術
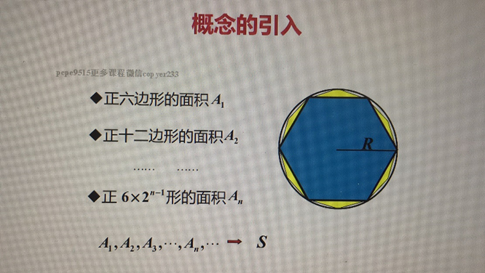

還可以表示為 xn= 1- 1/(2^n)
因為棒長是固定1 減去最後一天剩下的 也是擷取的總長
1-1/(2^n)無限趨近於1
數列的定義
·按自然數1,2,3,…編號依次排列的一列數 x1 x2 … xn … 稱為無窮數列 簡稱數列
·其中每個數稱為數列的項,xn稱為通項(一般項) 此數列可記為{xn}
例如 2 4 8 …2^n… {2^n}
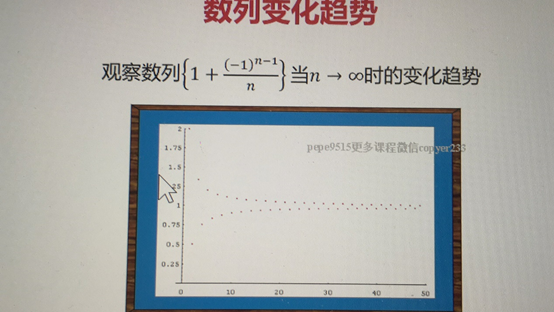
問題
·當n無限增大時 xn是否無限接近某一確定的數指
上面實驗 當n無限增大時 數列{1+ ( (-1)^(n-1) )/n
問題
·無限接近意味著什麼 如何用數學語言刻畫它

數列的極限
·如果對於任意給定的正數e(不論它多麼小)
·總存在正整數N,
·使得對於n>N時的一切xn
·不等式|xn-a|<e都成立,
那麼就稱常數a是數列xn的極限 或者稱數列xn收斂於a
記為lim n->∞ xn = a (或xn ->a(n->∞))
注意
·注1:如果數列沒有極限,就說數列是發散的(不收斂的
·注2:不等式|xn-a|<e 刻畫了xn與a無限接近
·注3:定義中正整數N與任意給定的正數e有關
數列極限的幾何解釋
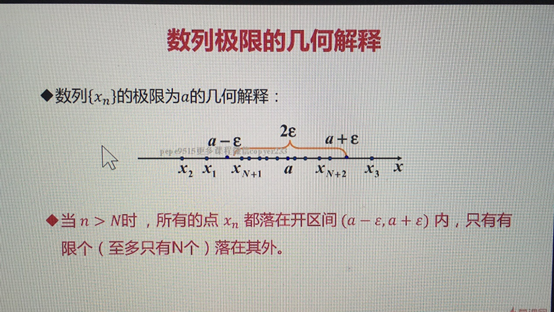
將a表示出來 然後做a的鄰域
當n>N的時候,所有的點都會落入到橘黃色的開區間內 只有有限個(至多有N個 不大於大N的)落在其外
e-N語言
任意符號(把A倒置過來
存在符號(把E反轉過來
·數列極限定義並未給出求極限的方法
例題1:

例題2:

例題3:

數列的極限
·如果對於任意給定的正數 (不論它多麼小)
·總存在正整數N,
·使得對於n>N時的一切xn
·不等式|xn-a|<都成立,
那麼就稱常數a是數列xn的極限 或者稱數列xn收斂於a
記為lim n->∞ xn = a (或xn ->a(n->∞))
二、收斂數列的性質
收斂:有極限
發散:無極限
收斂數列的性質:
1.有界性
·對數列xn 若存在正數M
·使得一切自然數n 恆有|xn|<M成立
則稱數列xn有界,否則,稱為無界
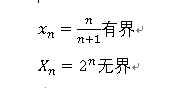
有界
無界
定理一 收斂的數列必定有界
證明: 
由定義,取
則 使得當n>N時 恆有|xn-a|<1 即有a-1<xn<a+1
記M= max{|x1|,…,|xn|,|a-1|,|a+1|}
則對一切自然數n,皆有|xn|<M,故{xn}有界
注:有界性是數列收斂的必要條件
2.唯一性
定理2 每個收斂的數列只有一個極限
3.保號性
如果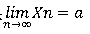
且a>0(或a<0) 那麼存在正整數N>0 當n>N時
都有xn>0(或xn<0)
4.收斂數列與其子數列間的關係
如果數列收斂於a,則它的任一子數列也收斂 且極限也是a
4.收斂數列與其子數列間的關係
如果數列收斂於a,則它的任一子數列也收斂 且極限也是a
