[大神貼]卷積:如何成為一個很厲害的神經網路
什麼是卷積神經網路?又為什麼很重要?
卷積神經網路(Convolutional Neural Networks, ConvNets or CNNs)是一種在影象識別與分類領域被證明特別有效的神經網路。卷積網路已經成功地識別人臉、物體、交通標誌,應用在機器人和無人車等載具。
 圖1
圖1
在上面的圖1當中,卷積網路能夠識別場景而系統可以自動推薦相關標籤如“橋”、“鐵路”、“網球”等。圖2則展示了卷積網路識別日常事物如人、動物的例子。最近,卷積網路也已經在自然語言處理上顯示出了威力(比如句子分類)。
 圖2
圖2
卷積網路,在今天的絕大多數機器學習應用中都是極重要的工具。但是,理解卷積網路並首次學著使用,這體驗有時並不友好。本文的主旨在於幫助讀者理解,卷積神經網路是如何作用於圖片的。
如果你對神經網路還是完全陌生的,建議閱讀9行Python程式碼搭建神經網路來掌握一些基本概念。在本文,多層感知機(Multi-Layer Perceptrons, MLP)也被記作全連線層(Fully Connected Layers)。
LeNet架構(1990年代)
LeNet是最早用於深度學習了領域的卷積神經網路之一。Yann LeCun的這一傑作LeNet5得名於他自1988年以來的系列成功迭代。彼時LeNet架構還主要被用於識別郵政編碼等任務。
下面我們將直觀地感受一下,LeNet是如何學習識別影象的。近幾年已經出現了很多建立在LeNet之上的新架構,但是基本概念還是來自於LeNet,並且理解了LeNet再學其他的也會更簡單。
 圖3:簡單的ConvNet
圖3:簡單的ConvNet
圖3的卷積神經網路與LeNet的原始架構十分接近,把圖片分入四個類別:狗,貓,船,鳥(LeNet最早主要就是用來做這些)。如上圖所示,當獲得一張船圖作為輸入的時候,網路正確的給船的分類賦予了最高的概率(0.94)。輸出層的各個概率相加應為1.
圖3的卷積神經網路主要執行了四個操作:
- 卷積
- 非線性(ReLU)
- 池化或下采樣
- 分類(全連線層)
這些操作也是所有卷積神經網路的基石,所以理解好這些工作對於理解整個神經網路至關重要。接下來我們將嘗試最直觀地理解以上操作。
圖片是畫素值的矩陣
本質上來講,每個圖片都可以表示為畫素值組成的矩陣
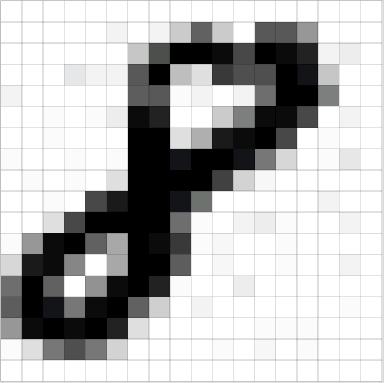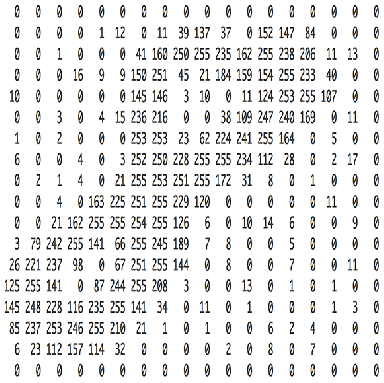 圖4:畫素值矩陣
圖4:畫素值矩陣
通道是代指圖片特定成分的習語。常見數碼相機拍出來的照片有三個通道——紅、綠、藍-可以想象為是三個2d矩陣(每種顏色對應一個)疊在一起,每個矩陣的值都在0-255之間。
另一方面,灰度影象只有單通道。本文為簡單起見只考慮灰度影象,這樣就是一個2d矩陣。矩陣中的每個畫素值還是0到255——0表示黑,255表示白。
卷積
卷積網路是因為“卷積”操作而得名的。卷積的根本目的是從輸入圖片中提取特徵。卷積用一個小方陣的資料學習影象特徵,可以保留畫素之間的空間關係。這裡不深入探討卷積的數學原理,重在理解工作過程。
如上所述,每個圖片都是畫素值矩陣。考慮一個5x5的影象,其畫素值為0和1,下面的綠色矩陣是灰度圖的特例(常規灰度圖的畫素值取值0-255),同時考慮如下的3x3矩陣:

然後,5x5影象和3x3矩陣之間的卷積計算,可由下圖的動畫所表示:
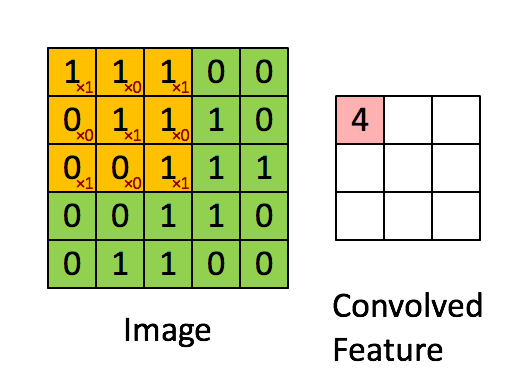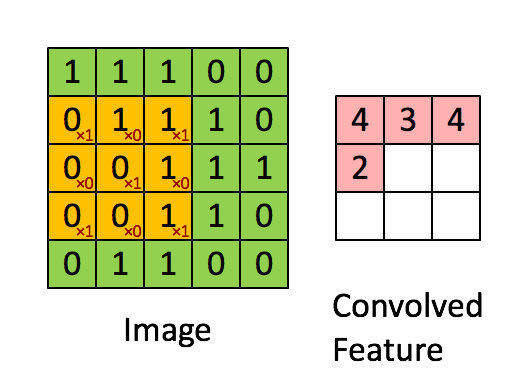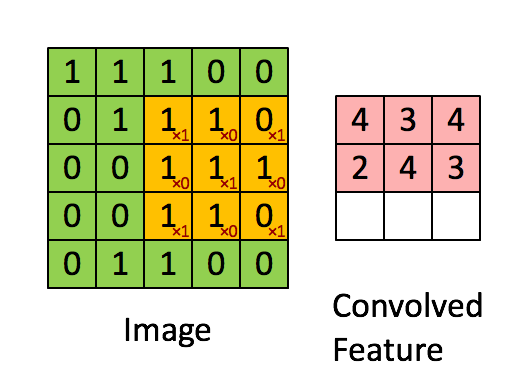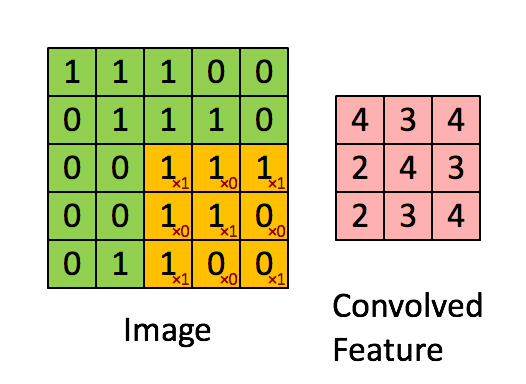 圖5:卷積操作。輸出矩陣叫卷積特徵或特徵對映
圖5:卷積操作。輸出矩陣叫卷積特徵或特徵對映
想一想以上操作是如何完成的,我們在原始圖片(綠色)上1畫素、1畫素地滑動橙色矩陣(也稱'stride'),並且在每個位置上,我們都對兩個矩陣的對應元素相乘後求和得到一個整數,這就是輸出矩陣(粉色)的元素。注意,3x3矩陣每次只“看見”輸入圖片的一部分。
3x3矩陣也叫“濾波器”、“核”或“特徵探測器”,在原圖上滑動濾波器、點乘矩陣所得的矩陣稱為“卷積特徵”、“激勵對映”或“特徵對映”。這裡的重點就是,理解濾波器對於原輸入圖片來說,是個特徵探測器。
對於同一張照片,不同的濾波器將會產生不同的特徵對映。比如考慮下面這張輸入圖片:

下表可見各種不同卷積核對於上圖的效果。只需調整濾波器的數值,我們就可以執行諸如邊緣檢測、銳化、模糊等效果——這說明不同的濾波器會從圖片中探測到不同的特徵,比如邊緣、曲線等。

另一種對卷積操作很好的理解方式就是觀察圖6的動畫:
 圖6:卷積操作
圖6:卷積操作
一個濾波器(紅框)在圖片上滑動(卷積)產生特徵對映。在同一個圖片上,另一個濾波器(綠框)的卷積產生了不同的特徵對映。須知,卷積操作捕捉的是原圖的區域性依賴性。另外,注意觀察兩個不同的濾波器怎樣產生不同的特徵對映。其實不管是圖片,還是兩個濾波器,本質上都不過是我們剛才看過的數值矩陣而已。
在實踐當中,卷積神經網路在訓練過程中學習濾波器的值,當然我們還是要在訓練之前需要指定一些引數:濾波器的個數,濾波器尺寸、網路架構等等。濾波器越多,從影象中提取的特徵就越多,模式識別能力就越強。
特徵對映的尺寸由三個引數控制,我們需要在卷積步驟之前就設定好:
- 深度(Depth): 深度就是卷積操作中用到的濾波器個數。如圖7所示,我們對原始的船圖用了三個不同的濾波器,從而產生了三個特徵對映。你可以認為這三個特徵對映也是堆疊的2d矩陣,所以這裡特徵對映的“深度”就是3。
 圖7
圖7
-
步幅(Stride):步幅是每次滑過的畫素數。當
Stride=1的時候就是逐個畫素地滑動。當Stride=2的時候每次就會滑過2個畫素。步幅越大,特徵對映越小。 -
補零(Zero-padding):有時候在輸入矩陣的邊緣填補一圈0會很方便,這樣我們就可以對影象矩陣的邊緣畫素也施加濾波器。補零的好處是讓我們可以控制特徵對映的尺寸。補零也叫寬卷積,不補零就叫窄卷積。
非線性
如圖3所示,每個卷積操作之後,都有一個叫ReLU的附加操作。ReLU的全稱是糾正線性單元(Rectified Linear Unit),是一種非線性操作,其輸出如下:
 圖8:ReLU
圖8:ReLU
ReLU是以畫素為單位生效的,其將所有負值畫素替換為0。ReLU的目的是向卷積網路中引入非線性,因為真實世界裡大多數需要學習的問題都是非線性的(單純的卷積操作時線性的——矩陣相乘、相加,所以才需要額外的計算引入非線性)。
圖9可以幫助我們清晰地理解,ReLU應用在圖6得到的特徵對映上,輸出的新特徵對映也叫“糾正”特徵對映。(黑色被抹成了灰色)
 圖9:ReLU
圖9:ReLU
其他非線性方程比如tanh或sigmoid也可以替代ReLU,但多數情況下ReLU的表現更好。
池化
空間池化(也叫亞取樣或下采樣)降低了每個特徵對映的維度,但是保留了最重要的資訊。空間池化可以有很多種形式:最大(Max),平均(Average),求和(Sum)等等。
以最大池化為例,我們定義了空間上的鄰域(2x2的窗)並且從糾正特徵對映中取出窗裡最大的元素。除了取最大值以額外,我們也可以取平均值(平均池化)或者把窗裡所有元素加起來。實際上,最大池化已經顯示了最好的成效。
圖10顯示了對糾正特徵對映的最大池化操作(在卷積+ReLU之後),使用的是2x2的窗。
 圖10:最大池化
圖10:最大池化
我們以2格的步幅(Stride)滑動2x2的窗,並且取每個區域的最大值。圖10同樣顯示了池化可以減少特徵對映的維度。
在圖11所示的網路中,池化操作分別應用於每個特徵對映(注意正因如此,我們從三個輸入對映得到了三個輸出對映)。
 圖11:對糾正特徵對映應用池化
圖11:對糾正特徵對映應用池化
圖12即為池化操作施加在圖9所得糾正特徵對映上的效果。
 圖12:池化
圖12:池化
池化的功能室逐步減少輸入表徵的空間尺寸。特別地,池化
- 使輸入表徵(特徵維度)更小而易操作
- 減少網路中的引數與計算數量,從而遏制過擬合
- 增強網路對輸入影象中的小變形、扭曲、平移的魯棒性(輸入裡的微小扭曲不會改變池化輸出——因為我們在區域性鄰域已經取了最大值/平均值)。
- 幫助我們獲得不因尺寸而改變的等效圖片表徵。這非常有用,因為這樣我們就可以探測到圖片裡的物體,不論那個物體在哪。
截至目前:
 圖13
圖13
至此我們已經瞭解了卷積、ReLU和池化是如何運轉的,這些層對於所有的卷積神經網路都是最基礎的單元。如圖13所示,我們有兩組“卷積+ReLU+池化”層——其中第二組對第一組的輸出施加了六個濾波器,產生了六個特徵對映。ReLU分別作用域這六個特徵對映,再對生成的糾正特徵對映使用最大池化。
這些層合力提取出有用的特徵,為網路引入了非線性並降低了維度,還使特徵對尺寸和平移保持不變性。
第二個池化層的輸出相當於全連線層的輸入,我們將在下一節繼續探討。
全連線層
全連線層(Fully Connected layer)就是使用了softmax激勵函式作為輸出層的多層感知機(Multi-Layer Perceptron),其他很多分類器如支援向量機也使用了softmax。“全連線”表示上一層的每一個神經元,都和下一層的每一個神經元是相互連線的。
卷積層和池化層呢個的輸出代表了輸入影象的高階特徵,全連線層的目的就是用這些特徵進行分類,類別基於訓練集。比如圖14所示的影象分類任務,有四種可能的類別。(注意,圖14沒有顯示出所有的神經元節點)
 圖14:全連線層——每個節點都與相鄰層的所有節點相連
圖14:全連線層——每個節點都與相鄰層的所有節點相連
除了分類以外,加入全連線層也是學習特徵之間非線性組合的有效辦法。卷積層和池化層提取出來的特徵很好,但是如果考慮這些特徵之間的組合,就更好了。
全連線層的輸出概率之和為1,這是由激勵函式Softmax保證的。Softmax函式把任意實值的向量轉變成元素取之0-1且和為1的向量。
聯合起來——反向傳播訓練
綜上,卷積+池化是特徵提取器,全連線層是分類器。
注意圖15,因為輸入圖片是條船,所以目標概率對船是1,其他類別是0.
- 輸入影象 = 船
- 目標向量 = [0, 0, 1 ,0]
 圖15:訓練卷積神經網路
圖15:訓練卷積神經網路
卷積網路的訓練過程可以概括如下:
- Step 1: 用隨機數初始化所有的濾波器和引數/權重
-
Step 2: 網路將訓練圖片作為輸入,執行前向步驟(卷積,ReLU,池化以及全連線層的前向傳播)並計算每個類別的對應輸出概率。
- 假設船圖的輸出概率是
[0.2, 0.4, 0.1, 0.3] - 因為第一個訓練樣本的權重都是隨機的,所以這個輸出概率也跟隨機的差不多
- 假設船圖的輸出概率是
-
Step 3: 計算輸出層的總誤差(4類別之和)
- 總誤差=∑12(目標概率−輸出概率)2總誤差=∑12(目標概率−輸出概率)2
-
Step 4: 反向傳播演算法計算誤差相對於所有權重的梯度,並用梯度下降法更新所有的濾波器/權重和引數的值,以使輸出誤差最小化。
- 權重的調整程度與其對總誤差的貢獻成正比。
- 當同一影象再次被輸入,這次的輸出概率可能是
[0.1, 0.1, 0.7, 0.1],與目標[0, 0, 1, 0]更接近了。 - 這說明我們的神經網路已經學習著分類特定圖片了,學習的方式是調整權重/濾波器以降低輸出誤差。
- 如濾波器個數、濾波器尺寸、網路架構這些引數,是在Step 1之前就已經固定的,且不會在訓練過程中改變——只有濾波矩陣和神經元突觸權重會更新。
以上步驟訓練了卷積網路——本質上就是優化所有的權重和引數,使其能夠正確地分類訓練集裡的圖片。
當一個新的(前所未見的)的圖片輸入至卷積網路,網路會執行前向傳播步驟並輸出每個類別的概率(對於新影象,輸出概率用的也是訓練過的權重值)。如果我們的訓練集足夠大,網路就有望正確分類新圖片,獲得良好的泛化(generalization)能力。
注意 1: 以上步驟已被極大簡化,且數學細節均以忽略,這是為了讓訓練過程更直觀。
注意 2: 上例中,我們用了兩組卷積+池化層,其實這些操作可以在一個卷積網路內重複無數次。如今有些表現出眾的卷積網路,都有數以十計的卷積+池化層!並且,不是每個卷積層後面都要跟個池化層。由圖16可見,我們可以有連續多組卷積+ReLU層,後面再加一個池化層。
 圖16
圖16
視覺化卷積神經網路
一般來說,卷積層越多,能學會的特徵也就越複雜。比如在影象分類中,一個卷積神經網路的第一層學會了探測畫素中的邊緣,然後第二層用這些邊緣再去探測簡單的形狀,其他層再用形狀去探測高階特徵,比如臉型,如圖17所示——這些特徵是Convolutional Deep Belief Network學得的。這裡只是一個簡單的例子,實際上卷積濾波器可能會探測出一些沒有意義的特徵。
 圖17:Convolutional
Deep Belief Network學習的特徵
圖17:Convolutional
Deep Belief Network學習的特徵
Adam Harley做了一個非常驚豔的卷積神經網路視覺化,這個網路是用MNIST手寫數字資料庫訓練而來的。我強烈推薦大家玩一玩,以便更深地理解卷積神經網路的細節。
如下我們將看到網路是如何識別輸入數字"8"的。注意,圖18沒有把ReLU過程單獨顯示出來。
 圖18:視覺化卷積神經網路
圖18:視覺化卷積神經網路
輸入影象有1024個畫素(32x32圖片),第一個卷積層(Convolution Layer 1)有六個不同的5x5濾波器(Stride = 1)。由圖可見,六個不同的濾波器產生了深度為6的特徵對映。
Convolutional Layer 1 後面跟著Pooling Layer 1, 對六個特徵對映分別進行2x2的最大池化(Stride = 2)。你可以在動態網頁中的每個畫素上活動滑鼠指標,觀察其在前一個卷積層裡對應的4x4網格(如圖19)。不難發現,每個4x4網格里的最亮的畫素(對應最大值)構成了池化層。
 圖19:視覺化池化操作
圖19:視覺化池化操作
之後我們有三個全連線(FC)層:
- FC 1: 120神經元
- FC 2: 100神經元
- FC 3: 10神經元,對應10個數字——也即輸出層
在圖20,輸出層10個節點中的每一個,都與第二個全連線層的100個節點相連(所以叫“全連線”)。
注意輸出層裡的唯一的亮點對應著8——這說明網路正確的識別了手寫數字(越亮的節點代表越高的概率,比如這裡8就擁有最高的概率)。
 圖20:視覺化全連線層
圖20:視覺化全連線層
該視覺化的3D版可見於這裡。
其他卷積網路架構
卷積神經網路始自1990年代起,我們已經認識了最早的LeNet,其他一些很有影響力的架構列舉如下:
-
1990s至2012:從90年代到2010年代早期,卷積神經網路都處於孵化階段。隨著資料量增大和計算能力提高,卷積神經網路能搞定的問題也越來越有意思了。
-
AlexNet(2012):2012年,Alex Krizhevsky釋出了AlexNet,是LeNet的更深、更寬版本,並且大比分贏得了當年的ImageNet大規模影象識別挑戰賽(ILSVRC)。這是一次非常重要的大突破,現在普及的卷積神經網路應用都要感謝這一壯舉。
-
ZF Net(2013):2013年的ILSVRC贏家是Matthew Zeiler和Rob Fergus的卷積網路,被稱作ZF Net,這是調整過架構超引數的AlexNet改進型。
-
GoogleNet(2014):2014的ILSVRC勝者是來自Google的Szegedy et al.。其主要貢獻是研發了Inception Module,它大幅減少了網路中的引數數量(四百萬,相比AlexNet的六千萬)。
-
VGGNet(2014):當年的ILSVRC亞軍是VGGNet,突出貢獻是展示了網路的深度(層次數量)是良好表現的關鍵因素。
-
ResNet(2015): Kaiming He研發的Residual Network是2015年的ILSVRC冠軍,也代表了卷積神經網路的最高水平,同時還是實踐的預設選擇(2016年5月)。
-
DenseNet(2016年8月): 由Gao Huang發表,Densely Connected Convolutional Network的每一層都直接與其他各層前向連線。DenseNet已經在五個高難度的物體識別基礎集上,顯式出非凡的進步。
(翻譯部分 完)
經過本文和之前的系列文章,您應該已經掌握了卷積神經網路的基本原理。接下來我們嘗試用流行的Python深度學習庫Keras,動手實地搭建一個LeNet。
實踐是神經網路的唯一標準
回顧LeNet的架構,補全第二組卷積+激勵+池化,搭建出經典的LeNet網路。
提示:
- 第二組卷積層有
16個濾波器,尺寸為8x8。 - 第二組激勵層使用
tanh函式 - 第二組最大池化層的尺寸和步幅均為
3x3
請在下方的Python開發環境中補全程式碼,並點選藍色按鈕執行檢查答案是否正確。
Python 3 LeNet with Keras 1# 匯入相關模組
2
from keras.models import Sequential
3
from keras.layers.convolutional import Convolution2D, MaxPooling2D
4
from keras.layers.core import Activation, Flatten, Dense
5
6
7
# 卷積網路搭建
8
model = Sequential()
9
10
# 第一組卷積+池化
11
model.add(Convolution2D(nb_filter=6, nb_row=5, nb_col=5,
12
input_shape=(32, 32, 1)))
13
model.add(Activation('relu'))
14
model.add(MaxPooling2D(pool_size=(2,2), strides=(2,2)))
15
16
17
# 第二組卷積+池化
18
# 程式碼補完
19
20
21
22
23
# 程式碼補完
24
25
26
# 全連線層
27
model.add(Flatten())
28
model.add(Dense(120))
29
model.add(Dense(100))
30
model.add(Dense(10))
31
model.add(Activation('softmax'))
