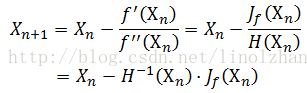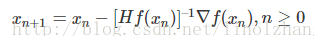牛頓法 主要有兩方面的應用：

1. 求方程的根；

2. 求解最優化方法；

一. 為什麼要用牛頓法求方程的根？

       問題很多，牛頓法 是什麼？目前還沒有講清楚，沒關係，先直觀理解為 牛頓法是一種迭代求解方法（Newton童鞋定義的方法）。

       假設 f(x) = 0 為待求解方程，利用傳統方法求解，牛頓法求解方程的公式：

f(x0+Δx) = f(x0) +f′(x0) Δx

即 f(x) = f(x0) + f′(x0) (x-x0)

       公式可能大家會比較熟悉，一階泰勒展式，f′(a) 表示 f(x) 在 x0 點的斜率 （這個很好理解），當X方向增量（Δx

x = x0 - f(x0) / f′(x0)    =>   xn+1 = xn - f(xn) / f′(n)

       通過逐次迭代，牛頓法 將逐步逼近最優值，也就是方程的解。

二. 擴充套件到最優化問題

       這裡的最優化 是指非線性最優化，解非線性最優化的方法有很多，比如 梯度下降法、共軛梯度法、變尺度法和步長加速法 等，這裡我們只講 牛頓法。

       針對上面問題進行擴充套件：

       解決 f(x) = 0 的問題

f(x) = f(x0) + f'(x0)*(x-x0) + o( (x-x0)^2 )

           去掉末位高階展開項，代入x = x0+Δx，得到：

f(x) = f(x0+Δx) = f(x0) + f′(x0) Δx

       那麼 要解決 f′(x) = 0 的問題，我們就需要二階泰勒展開：

f(x) = f(x0) + f'(x0)*(x-x0) + 0.5*f''(x0)*(x-x0)^2 + o( (x-x0)^3 )

           去掉末位高階展開項，代入x = x0+Δx，得到：

f(x) = f(x0+Δx) = f(x0) + f′(x0)Δx + 0.5 * f′′(x0) (Δx)^2

       求導計算： f′(x) = f'(x0+Δx) = 0，得到：

 [ f(x0) + f′(x0)(x−x0) + 0.5 f′′(x0)(x−x0)^2 ]′ = 0

       整理：

 f′(x0) + f′′(x0)(x−x0) = 0

x = x0 − f′(x0) / f′′(x0)   =>  xn+1 = xn - f'(xn) / f'′(xn)

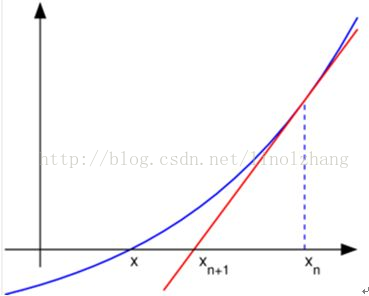
       牛頓法 一圖總結為：

三. 牛頓法 與 Hessian矩陣的關係

       以上牛頓法的推導 是針對 單變數問題，對於多變數的情況，牛頓法 演變為：

      與上面的單變量表示方式類似，需要用到變數的 一階導數 和 二階導數。

      其中 J 定義為 雅克比矩陣，對應一階偏導數。

      H 為 Hessian矩陣，對應二階偏導數。

       網上也能搜到類似的公式表達，也列出來：

       牛頓法 在多變數問題上仍然適用迭代求解，但Hessian矩陣的引入增加了複雜性，特別是當：

▪ Hessian 矩陣非正定（非凸）導致無法收斂；

▪ Hessian 矩陣維度過大帶來巨大的計算量。

       針對這個問題，在 牛頓法無法有效執行的情況下，提出了很多改進方法，比如 擬牛頓法（Quasi-Newton Methods）可以看作是牛頓法的近似。

       擬牛頓法 只需要用到一階導數，不需要計算Hessian矩陣 以及逆矩陣，因此能夠更快收斂，關於 擬牛頓法 這裡不再具體展開，也有更深入的 DFP、BFGS、L-BFGS等演算法，大家可以自行搜尋學習。

       總體來講，擬牛頓法 都是用來解決 牛頓法 本身的 複雜計算、難以收斂、區域性最小值等問題。

原地址：http://blog.csdn.net/linolzhang/article/details/60151623