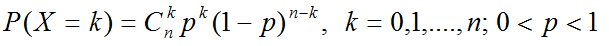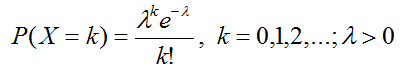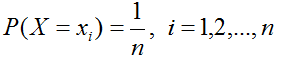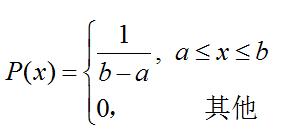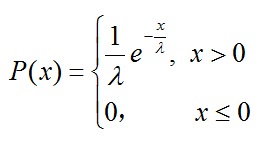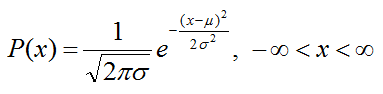3 概率分佈與隨機函式
更多MATLAB資料分析視訊請點選，或者在網易雲課堂上搜索《MATLAB資料分析與統計》 http://study.163.com/course/courseMain.htm?courseId=1003615016
隨著計算機技術的快速發展，隨機數在越來越多的領域得到了廣泛應用，例如資訊保安，網路遊戲，計算機模擬和模擬計算，這一章將介紹常用的概率分佈及概率計算、利用MATLAB生成隨機數。
1.概率分佈及概率計算
1.1 概率分佈的定義
設X為一隨機變數，對任意實數x，定義
F（x）=P（X<=x）
為X的分佈函式。根據隨機變數取值的特定，隨機變數分為離散型和連續型兩種。P為X的概率函式
1.2 幾種常見的概率分佈
（1）二項分佈
若隨機變數X的概率函式為
則稱X服從二項分佈，記為X~B（n，p）。其期望E（X）=np，方差var（X）=np（1-p）。
（2）泊松分佈
若隨機變數X的概率函式為
則稱X服從引數為λ的泊松分佈，記為X~P（λ）。其期望E（x）=λ，方差var（X）=λ。
（3）離散均勻分佈
若隨機變數X的概率函式為
則稱X服從離散的均勻分佈
（4）連續均勻分佈
若隨機變數X的概率密度函式為
則稱X服從區間[a,b]上的連續均勻分佈，記為X~U（a，b）。其期望E（X）=（a+b）/2，方差var(X)=(b-a)^2/12.
（5）指數分佈
若隨機變數X的概率密度函式為
其中λ>0為引數，則稱X服從指數分佈，記為X~Exp（λ）。其期望E（X）=λ，方差var（x）=λ^2
（6）正態分佈
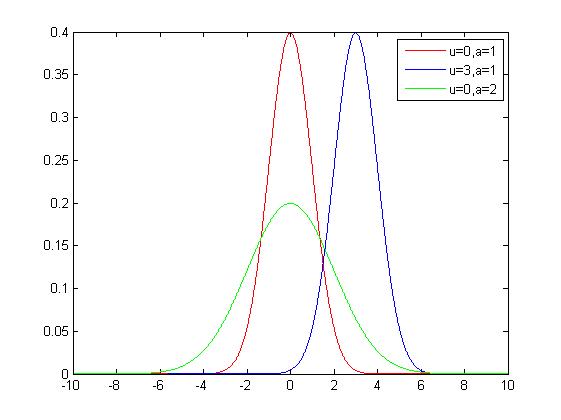
若隨機變數X的概率密度函式為
其中，σ>0,μ為分佈引數，則稱X服從正態分佈，記為X~N（μ，σ^2）,其期望E（X）=μ，方差var（X）=σ^2。特別地，當μ=0，σ=1時，稱X服從標準正態分佈，記為X~N（0,1）。
（7）卡方分佈
若n個相互獨立的隨機變數ξ₁、ξ₂、……、ξn ，均服從標準正態分佈（也稱獨立同分佈於標準正態分佈），則這n個服從標準正態分佈的隨機變數的平方和
構成一新的隨機變數，其
卡方分佈
分佈規律稱為
分佈（chi-square distribution），其中引數n稱為自由度，正如正態分佈中均值或方差不同就是另一個正態分佈一樣，自由度不同就是另一個
分佈。記為
或者
.
卡方分佈是由正態分佈構造而成的一個新的分佈，當自由度n很大時，
分佈近似為正態分佈（8）t分佈
設隨機變數X與Y相互獨立，X服從N(0,1)分佈，Y服從自由度為k的卡方分佈，則稱隨機變數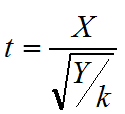
（9）F分佈
設隨機變數X和Y相互獨立，分別服從自由度為k1,和k2的卡方分佈，則稱隨機變數
1.3 概率密度、分佈函式和逆概率分佈函式值的計算
MATLAB統計工具箱中有這樣一系列函式，函式名以pdf三個字元結尾的函式用來計算常見連續分佈的密度函式值或離散分佈的概率函式值，函式名以cdf三個字串結尾的函式用來計算常見分佈的分佈函式值，函式名以inv三個字串結尾的函式用來計算常見分佈的逆概率分佈函式值。
MATLAB中常見分佈函式列表
離散分佈
二項分佈（bino）
負二項分佈（nbin）
幾何分佈（geo）
超幾何分佈（hyge）
泊松分佈（poiss）
離散均勻分佈（unid）
多項分佈（mn）
連續分佈
正態分佈（norm）
對數正態分佈（logn）
多元正態分佈（mvn）
連續均勻分佈（unif）
指數分佈（exp）
卡方分佈（chi2）
非中心卡方分佈（ncx2）
t分佈（t）
非中心t分佈（nct）
多元t分佈（mvt）
F分佈（F）
非中心F分佈（ncf）
威爾分佈（wbl）
瑞利分佈（rayl）
極值分佈（ev）
廣義極值分佈（gev）
.....
在列出的上面這些常見分佈名英文縮寫後面加上pdf，cdf ，inv 就可得到計算常見分佈的概率密度，分佈函式值和逆概率分佈函式值。
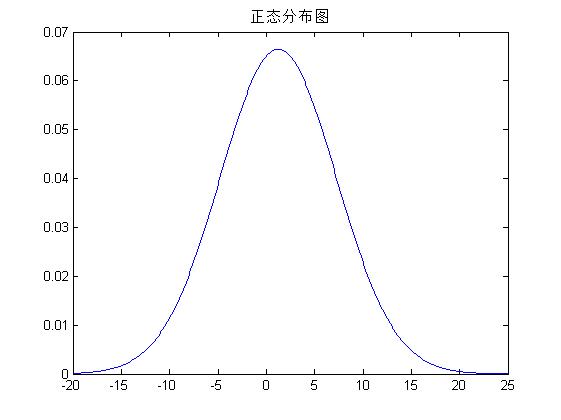
例：求服從均值為1.2345，標準差為6的正態分佈隨機變數X在x=0,1,2，.....，10處的密度函式值與分佈函式值，並求概率P（-2<X<=5）
%--首先畫出這個正態分佈圖
X=-20:0.1:25;
Y=normpdf(X,1.2345,6);
plot(X,Y);
title('正態分佈圖');
%定義一個x向量，然後求該向量對應處的概率密度值
x=0:10;
y=normpdf(x,1.2345,6)
%求x向量處所對應的分佈函式值
F=normcdf(x,1.2345,6)
%求概率P（-2<X<=5）
P=normcdf(5,1.2345,6)-normcdf(-2,1.2345,6)
y =
0.0651 0.0664 0.0660 0.0637 0.0598 0.0546 0.0485 0.0419 0.0352 0.0288 0.0229
F =
0.4185 0.4844 0.5508 0.6157 0.6776 0.7349 0.7865 0.8317 0.8703 0.9022 0.9280
P =
0.4399
2. 生成一元分佈隨機數
2.1 rand函式生成在 [0 ,1] 均勻分佈隨機數
呼叫格式： 說明
Y=rand（n） 生成nxn的隨機數矩陣
Y=rand（m，n） 生成mxn的隨機矩陣
Y=rand（[m n]） 生成mxn的隨機矩陣
Y=rand（m，n，p，....） 生成mxnxpx.....的隨機矩陣或陣列
Y=rand（[m n p ......]） 生成mxnxpx.....的隨機矩陣或陣列
Y=rand（size（A）） 生成與矩陣或陣列A具有相同大小的隨機數矩陣或陣列
其中，輸入引數m，n，p.....應為正整數，如果輸入負整數，則被認為是0，此時輸出一個空矩陣
例：呼叫rand函式生成10x10的隨機數矩陣，並將隨機數矩陣按列拉長，然後呼叫hist函式畫出頻數直方圖。
x=rand(10) %生成10行10列的隨機數矩陣，其元素在[0,1]上均勻分佈
x =
0.1427 0.8200 0.3579 0.7047 0.5575 0.5716 0.4143 0.6480 0.0531 0.7017
0.4089 0.3180 0.6729 0.3311 0.4346 0.8517 0.9439 0.3242 0.8149 0.6110
0.5818 0.3585 0.5933 0.5549 0.0934 0.6910 0.9925 0.4040 0.5675 0.3736
0.1233 0.7055 0.2608 0.2878 0.2139 0.8443 0.2135 0.7093 0.5351 0.7440
0.3646 0.7524 0.8828 0.3466 0.5959 0.2218 0.2759 0.9617 0.8090 0.0683
0.7368 0.9677 0.9340 0.7834 0.0744 0.8586 0.5181 0.6870 0.6267 0.3361
0.0374 0.0283 0.3005 0.2080 0.9345 0.3674 0.7654 0.8172 0.7334 0.0073
0.7945 0.7229 0.1999 0.5652 0.4904 0.5276 0.1047 0.1634 0.9903 0.5088
0.1943 0.8625 0.3562 0.4075 0.4936 0.7261 0.2309 0.9519 0.6459 0.0931
0.2711 0.6464 0.2895 0.1919 0.2751 0.0182 0.3102 0.3679 0.7707 0.2398
>> y=x(:); %將x按列拉長成一個了列向量
>> hist(y) %繪製頻數直方圖
>> xlabel('[0,1]上均勻分佈隨機數');
>> ylabel('頻數');
2.2 常見一元分佈隨機數
（1） MATLAB統計工具箱中函式名以rnd三個字串結尾的函式用來生成常見分佈的隨機數。如下表
函式名 說明
binornd 二項分佈隨機數
chi2rnd 卡方分佈隨機數
exprnd 指數分佈隨機數
frnd F分佈隨機數
lognrnd 對數分佈隨機數
mnrnd 多項分佈隨機數
normrnd 正態分佈隨機數
..................
例：
呼叫normrnd函式生成1000x3的正態分佈隨機函式，其中均值u=75，標準差為8，並畫出各列頻數直方圖
%呼叫normrnd函式生成1000行3列的隨機數矩陣x，其元素服從均值為75，標準差為8的正態分佈
>> x=normrnd(75,8,1000,3);%呼叫-rnd函式，需要傳遞給它分佈函式的引數，和生成矩陣的維數
>> figure;
>> hist(x); %繪製矩陣x每列的頻數直方圖
>> xlabel('正態分佈隨機數(\mu=75,\sigma=8)');
>> ylabel('頻數');
>> legend('第一列','第二列','第三列');
（2）random函式
random函式是一種通用的求各分佈的隨機數的函式，格式如下：
y=random（‘name’，A1，A2，A3，m，n）
name指定是那種分佈函式，取值為1.3中的 MATLAB中常見分佈函式列表
A1，A2，A3是分佈函式的引數
m，n用來指定生成隨機數的行和列
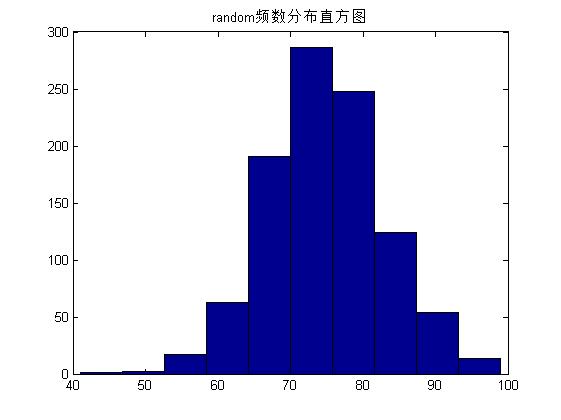
例：用normrnd和random函式分佈生成1000x1的正態分佈隨機函式，其中均值u=75，標準差為8，並畫出頻數直方圖
x=normrnd(75,8,1000,1); %normrnd函式生成均值u=75，標準差為8的正態隨機數
xx=random('norm',75,8,1000,1);%random函式生成均值u=75，標準差為8的正態隨機數
figure;
hist(x),title('normrnd頻數分佈直方圖');
>> figure;
>> hist(xx),title('random頻數分佈直方圖');
例：呼叫random函生成1000x1的二項分佈隨機數向量，然後做出頻率直方圖。二項分佈的引數為n=10，p=0.3
注意：如何計算頻率直返圖，首先呼叫ecdf函式就算出經驗累積概率分佈函式值，然後呼叫ecdfhist函式繪製頻率直方圖，其引數是ecdf函式的返回值
%呼叫random函式生成1000行1列的隨機數向量x，其元素服從二項式分佈B（10,0.3）
x=random('bino',10,0.3,1000,1);
[fp,xp]=ecdf(x);
ecdfhist(fp,xp,20);%50表示柱狀圖的個數，預設是10
>> xlabel('二項分佈（n=10，p=0.3）隨機數');
>> ylabel('f(x)');
2.3 任意一元分佈隨機數
（1）離散分佈隨機數
任給一個只取有限個值的離散總體X的分佈列
X x1 x2 ...... xn
P p1 p2 ........ pn
由函式randsample函式可以生成服從該分佈的隨機數。
y = randsample(n,k,true,w)
n表示取值向量
k生成隨機數的數量
true：用true表示有放回抽樣，false表示不放回抽樣
w：取值向量n所對應的概率，與n維度相同
例：設離散總體X的分佈列為
X -2 -1 0 1 2
P 0.05 0.2 0.5 0.2 0.05
呼叫randsample函式生成100個服從該分佈的隨機數，並呼叫tabulate函式統計各數字出現的頻數和頻率
xvalue=[-2 -1 0 1 2]; %定義取值向量
>> xp=[0.05 0.2 0.5 0.2 0.05]; %定義概率向量，與取值向量一一對應
>> %呼叫randsample函式生成100個服從指定離散分佈的隨機數
x=randsample(xvalue,100,true,xp);%用true表示有放回抽樣，false表示不放回抽樣
>> reshape(x,[10,10]) %把向量x裝換成10行10列的矩陣，便於觀察
ans =
2 0 1 2 1 0 1 0 1 0
0 1 -1 0 0 -2 2 -1 0 0
1 0 0 0 2 0 0 -1 -2 1
1 1 1 1 0 0 0 0 0 0
0 -1 1 -2 1 0 -1 0 2 0
1 0 1 -1 0 -1 -1 0 0 1
0 2 -1 1 -1 -1 -1 0 0 0
0 0 1 0 0 0 1 0 -1 -1
0 0 0 0 -2 0 0 -1 -2 -1
1 0 -1 0 0 -2 0 0 2 1
>> tabulate(x) %呼叫tabulate函式統計各數字出現的頻數和頻率
Value Count Percent
-2 6 6.00%
-1 17 17.00%
0 49 49.00%
1 21 21.00%
2 7 7.00%
從統計結果看， 隨機數的頻率分佈與真實分佈差距不大，但並不是完全一樣，當生成足夠多的隨機數時，會越來越接近真實分佈。
函式randsrc和randi也可以實現類似的功能。
（2）連續分佈隨機數
MATLAB統計工具箱中提供了slicesample函式，用來生成任意指定分佈隨機數
rand=slecesample（initial，nasample，‘pdf’，pdffun）
initial：指定一個初始值
nasample：產生隨機數的個數
‘pdf’：概率分佈函式
pdffun： 概率分佈函式的控制代碼
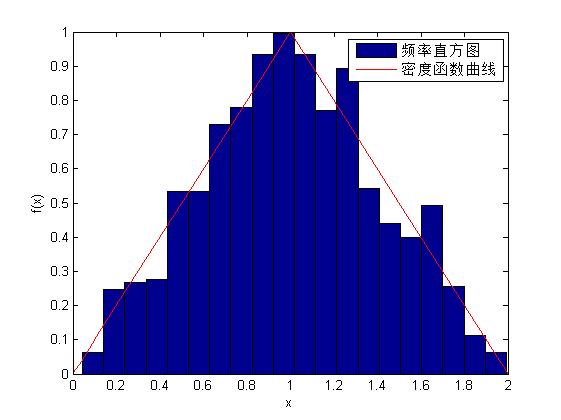
例：總體X服從拋物線分佈，其概率密度函式為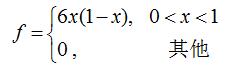
[email protected](x)6*x*(1-x); %用匿名函式方式定義密度函式,[email protected](x)6*x*(1-x)*(x>0&x<1)
%由於對於x>1或x<0的時候，pdffun<0,密度函不可能小於0，MATLAB會直接
%把pdffun=0，所以不需要寫成[email protected](x)6*x*(1-x)*(x>0&x<1)，但是對於
%其它情況下，還是需要指定x的範圍的，比如下一個例子
%呼叫slicesample函式生成1000個服從指定密度函式的隨機數
x=slicesample(0.5,1000,'pdf',pdffun);%指定初始值為0.5，需要{pdffun（0.5）>0}
[fp,xp]=ecdf(x); %計算經驗累積概率分佈函式值
ecdfhist(fp,xp,20); %繪製頻率直方圖
hold on;
fplot(pdffun,[0 1],'r'); %fplot用來繪製數學函式，plot是針對向量或矩陣的列來繪製曲線的
xlabel('x');
ylabel('f(x)');
legend('頻率直方圖','密度函式曲線');
例：總體X服從三角分佈，其概率密度函式為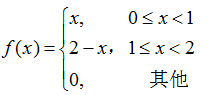
[email protected](x)x*(x>=0&x<1)+(2-x)*(x>=1&x<2); %密度函式
%呼叫slicesample函式生成1000個服從該分佈的隨機數
x=slicesample(1.5,1000,'pdf',pdffun);
[fp,xp]=ecdf(x); %計算經驗累積概率分佈函式值
ecdfhist(fp,xp,20); %繪製頻率直方圖
hold on;
fplot(pdffun,[0 2],'r'); %繪製真實密度函式曲線
xlabel('x');
ylabel('f(x)');
legend('頻率直方圖','密度函式曲線');
更多MATLAB資料分析視訊請點選，或者在網易雲課堂上搜索《MATLAB資料分析與統計》 http://study.163.com/course/courseMain.htm?courseId=1003615016