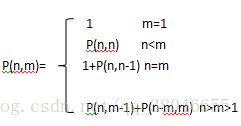問題描述：

問題描述 ：將一正整數劃分成一系列的正整數之和。
N=n1+n2+……+nk(n1>=n2>=n3….>=nk)
被稱為正整數n的一個劃分，一個正整數存在著不同的劃分。例如6
6=6

6=5+1

6=4+2 6=4+1+1

6=3+3 6=3+2+1 6=3+1+1+1

6=2+2+2 6=2+2+1+1 6=2+1+1+1+1

6=1+1+1+1+1+1

演算法分析：

若設P(n,m)表示正整數n的所有不同的劃分中，最大加數不大於m的劃分個數。
則可以建立一下遞迴：

(1)、P(n,1)=1，n>=1;

(2) P(n,m)=p(n,n),m>=n;

(3) P(n,n)=1+P(n,n-1);

(4)P(n,m)=P(n,m-1) + P(n-m,m), n>m>1

其上三種大家均可以理解，可唯獨第四個卻半懂非懂的，解釋一下第四個的分析：
“正整數n的最大加數不大於m的劃分數”可以理解成“n的最大加數不大於m-1的劃分數P(n,m-1)”和“n的最大加數為m的劃分數”之和。

舉例說明：P(6,4)等於“6的最大加數不大於3的劃分數P(6,3)”和“6的最大加數為4的劃分數”的和。而“6的最大加數為4的劃分數”為2，從上述例子也可以看出，也就是“6-4的最大加數不大於4的劃分數”，即為2，也就是P(6-4,4)=P(2,4)=2.

簡單來看，n的最大加數為m的劃分數不就是P(n-m,n-m),可以這樣理解，但這僅僅是一個特例，不可代表全部，如最大加數為2的劃分數呢，可以去試試。就會驚奇的發現結果就不是啦。
根據上述分析，可得到遞迴函式式：

#include<stdio.h>

int P(int n,int m){
    if(m==1 || n==1) return 1;
    if(m>n) return P(n,n);
    if(m==n) return 1+P(n,n-1);
    return P(n,m-1)+P(n-m,m);
} 
int main(){
    int
 
 n,s;
    printf("Please input a integer for getting the number of division\n");
    scanf("%d",&n);
    s = P(n,n);
    printf("The number is division of %d is %d\n",n,s);
    return 0;
}