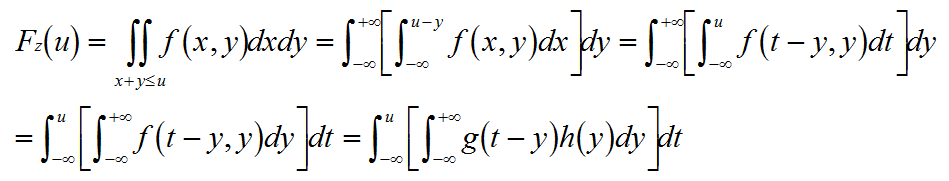中心極限定理是作為概率論的基礎定理，然而很多教科書都沒有給出完整證明或引證出處，嚴重影響到了學習的樂趣。通過在網上查詢資料，感謝網友的分享，最終根據傅立葉變換證明該定理，過程很簡短，也不要求有太深的數學知識面，下面給出定理的完整證明，首先介紹中心極限定理的定義
中心極限定理:
設隨機變數x1,x2,x3…xn相互獨立且滿足同一分佈，則隨機變數Yn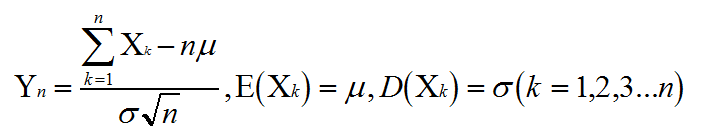
Yn的分佈函式Fn(x)

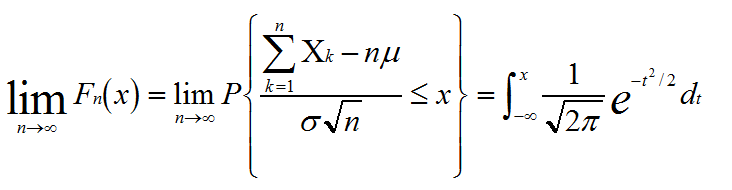
為了證明該定理設(X,Y)是二維連續隨機變數，且X,Y相互獨立其分佈函式分別為:

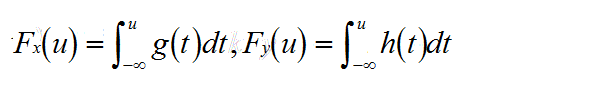
則(X,Y)的概率密度函式f(x,y)=g(x)h(y)，若隨機變數Z=X+Y，則Z的分佈函式Fz(u)=P{Z<=u}=P{X+Y<=u}

則Z的概率密度fz(u)為

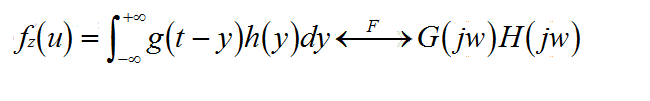
上式有兩點結論:1兩個獨立連續的隨機變數的和的概率密度函式是各自概率密度函式的卷積。2由卷積定理知道，和的概率密度函式的傅立葉變換等於各自概率密度函式的傅立葉變換的乘積。
設a,b為實數則(X+b)/a的分佈函式為

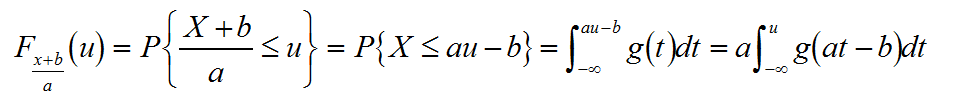
其概率密度以及對應的傅立葉變換為

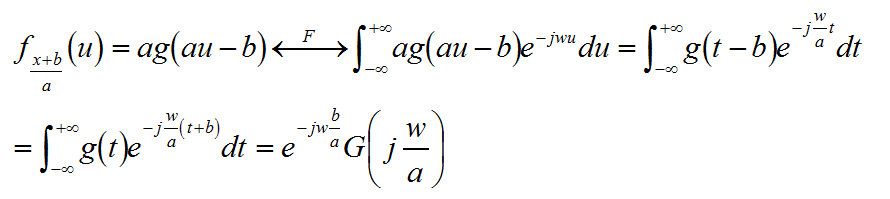
再根據中心極限定理的條件

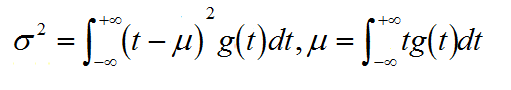
以及Yn

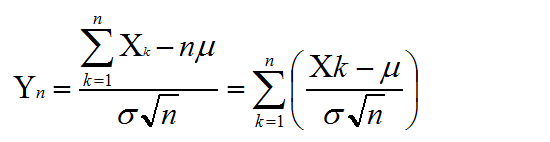
結合前面所得出的結論得到Yn的概率密度及其傅立葉變換

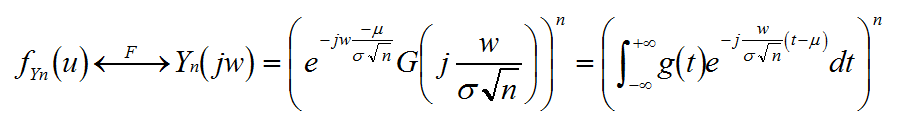
針對上式擴號中的被積函式進行泰勒分解

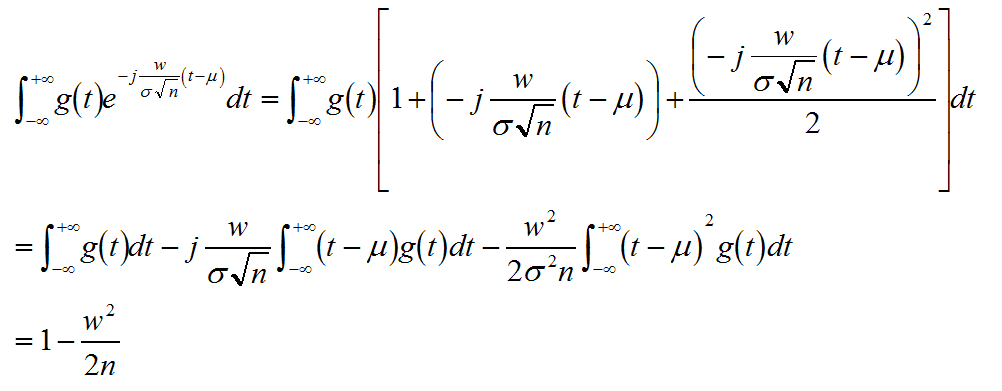
當n趨於無窮，根據傅立葉逆變換求Yn的概率密度

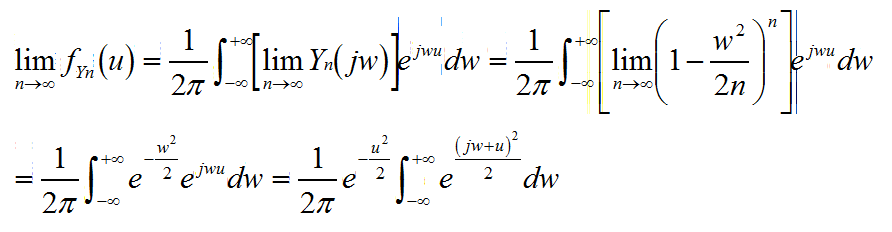
又因為

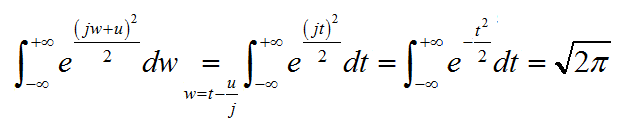
所以得到Yn的概率密度函式

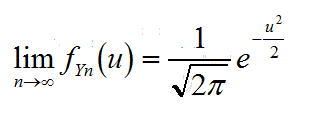
最終得到Yn的分佈

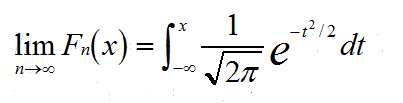
上面的證明非常簡短，在學習中心極限定理時確實被它震撼到了，它非常的強大。