Harris Corner Detector 公式推導以及具體含義
在做影象匹配時,常需要對兩幅影象中的特徵點進行匹配。為了保證匹配的準確性,所選擇的特徵必須有其獨特性,角點可以作為一種不錯的特徵。
那麼為什麼角點有其獨特性呢?角點往往是兩條邊緣的交點,它是兩條邊緣方向變換的一種表示,因此其兩個方向的梯度變換通常都比較大並且容易檢測到。
這裡我們理解一下Harris Corner 一種角點檢測的演算法
角點檢測基本原理:
人們通常通過在一個小的視窗區域內觀察點的灰度值大小來識別角點,如果往任何方向移動視窗都會引起比較大的灰度變換那麼往往這就是我們要找的角點。
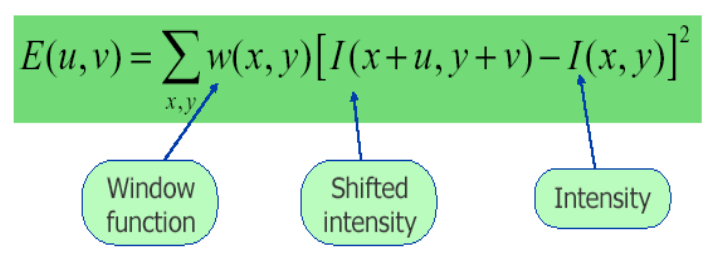
下面我們看一下Harris的數學公式,對於[x,y]平移[u,v]個單位後強度的變換有下式,I(x+u,y+v)是平移後的強度,I(x,y)是原影象畫素。對於括號裡面的值,如果是強度恆定的區域,那麼它就接近於零,反之如果強度變化劇烈那麼其值將非常大,所以我們期望E(u,v)很大。
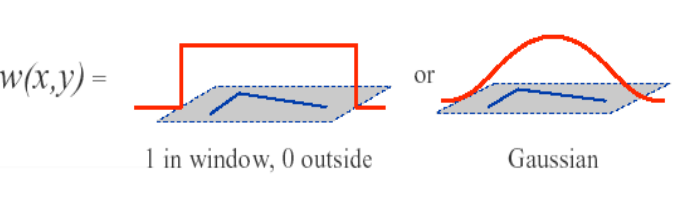
其中w是窗函式,它可以是加權函式,也可以是高斯函式
利用二維泰勒展開式我們有

所以其中一階可以近似為
![]()
於是我們可以給出Harris Corner的如下推導,其中Ix,Iy是x,y方向的Gradient模,乘以位移得到位移後的量

對於小的位移,我們可以用雙線性插值方法近似:
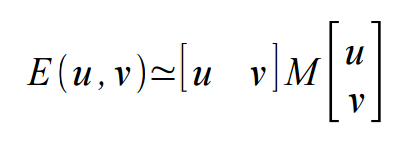
其中M為2*2矩陣如下
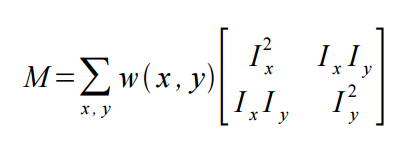
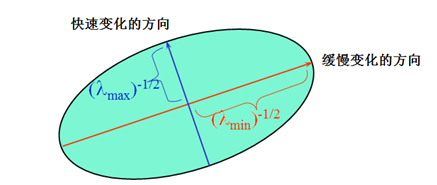
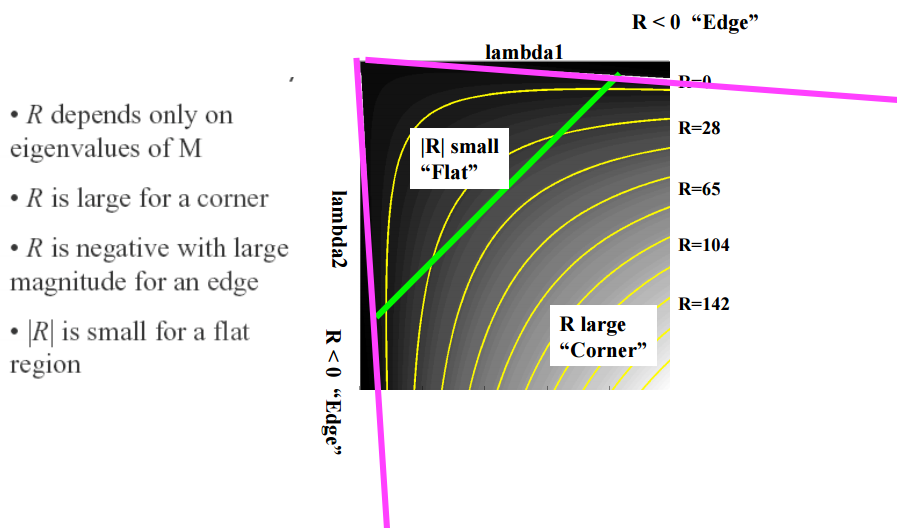
在本質上我們可以把二次項看成一個橢圓函式,我們對M進行特徵值分析有λ1,λ2
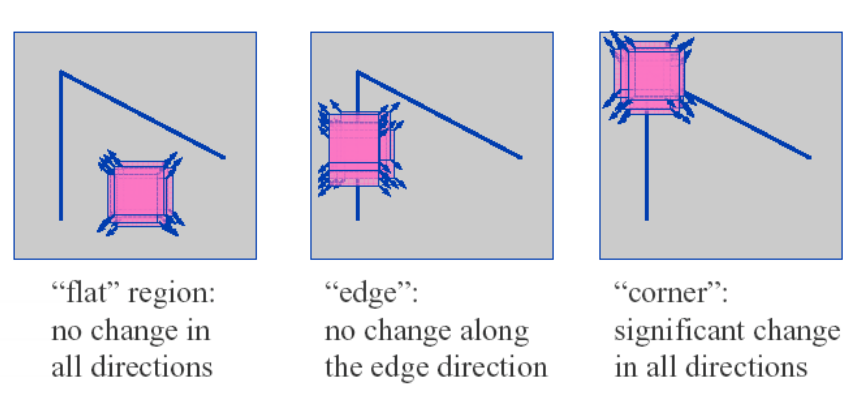
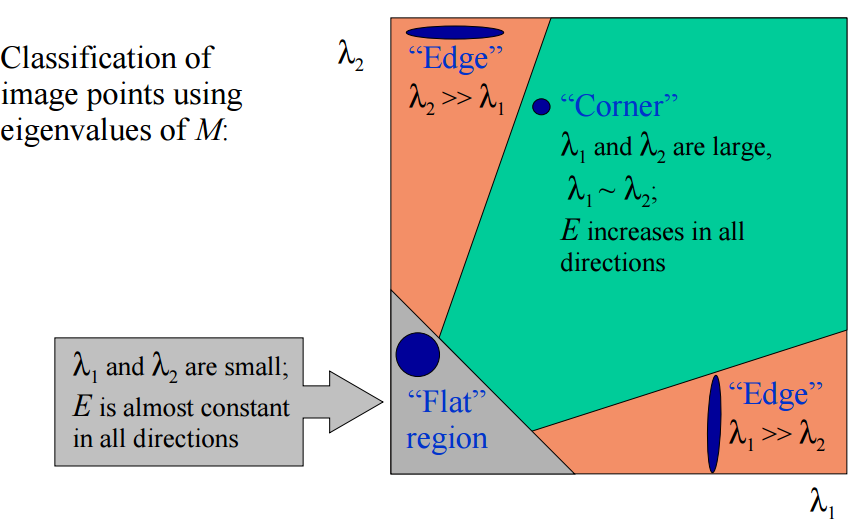
根據λ1,λ2的值我們可以把其分為三類:
1.λ1,λ2都很小且近似,E在所以方向接近於常數;
2.λ1>>λ2,或者λ2>>λ1, E將在某一方向上很大;
3.λ1,λ2都很大且近似,E將在所有方向上很大;
如圖所示:
最後我們通過計算角點響應值R來判斷其屬於哪個區間
![]()
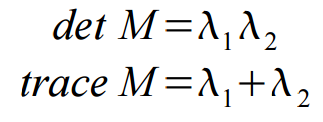
其中k一般為常數取在0.04-0.06間。
演算法步驟:
1.計算影象x,y方向的梯度Ix,Iy
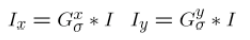
2.計算每個畫素點的梯度平方
![]()
3.計算梯度在每個畫素點的和
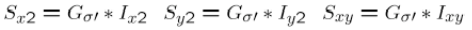
4.定義在每個畫素點的矩陣H,也就是前面的M
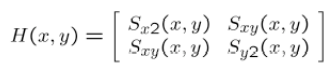
5.計算每個畫素的角點響應
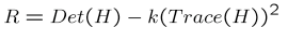
6.設定閾值找出可能點並進行非極大值抑制
程式碼:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
相關推薦Harris Corner Detector 公式推導以及具體含義在做影象匹配時,常需要對兩幅影象中的特徵點進行匹配。為了保證匹配的準確性,所選擇的特徵必須有其獨特性,角點可以作為一種不錯的特徵。 那麼為什麼角點有其獨特性呢?角點往往是兩條邊緣的交點,它是兩條邊緣方向變換的一種表示,因此其兩個方向的梯度變換通常都比較大並且容易 理解final static的使用場景以及具體含義public class TestStaticFinal { private static final String strStaticFinalVar = "aaa"; private static String strStaticVar = null; react中constructor( )和super( )的具體含義以及如何使用react中這兩個API出鏡率超級高,但是一直不太懂這到底是幹嘛的,有什麼用;今天整理一下,方便自己檢視同時方便大家。 1.constructor( )-----super( )的基本含義 constructor( )——構造方法 這是ES6對 根據經緯度計算兩點之間的距離的公式推導過程以及google.maps的測距函式首先,你要想了解清楚經緯度的具體定義,看完後再往下看,便會一目瞭然。 將地球看成一個球體,A(WA,JA)、B(WB,JB)兩點分別為兩個點的位置,其中W為緯度,J為經度,O為球心,球半徑為R,過A點畫出A的緯度圈並與B所在的經度相交與點C,分別過B、C兩點做球心O所在直線 POJ 2140 Herd Sums 公式推導cpp true typedef 因數 固定 ostream highlight ring sum 題意:給出n<=1e7 求有多少個連續數之和等於k x+x+1+....x+k=n (k+1)k/2+(k+1)x=n (k+1)k+(k+1)2x=2*n (k vijos - P1543極值問題(斐波那契數列 + 公式推導 + python)找到 span add gin python3 abi pri n) fill P1543極值問題 Accepted 標簽:[顯示標簽] 背景 小銘的數學之旅2。 描寫敘述 已知m、n為整數,且滿足下列兩個條件: ① vijos - P1302連續自然數和 (公式推導 + python).net ble tags ucid stat down bsp z-index fontsize P1302連續自然數和 Accepted 標簽:[顯示標簽] 描寫敘述 對一個給定的自然數M,求出所有的連續的自然數段(連續個數大於1) 解釋一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推導過程(轉載)線性不可分 itl 專註 out center forest 測試 重要 原因 KPCA,中文名稱”核主成分分析“,是對PCA算法的非線性擴展,言外之意,PCA是線性的,其對於非線性數據往往顯得無能為力,例如,不同人之間的人臉圖像,肯定存在非線性關系,自己做的基於ORL數據 SVM公式推導筆記svm width org sin .org 參考資料 zhang www http 參考資料: 對偶函數-http://blog.pluskid.org/?p=702 KTT和拉格朗日乘子-http://www.cnblogs.com/zhangchaoyan 反向傳播算法(過程及公式推導)不能 簡化 會有 geo 之前 代碼 求和 不同 eof 一、反向傳播的由來 在我們開始DL的研究之前,需要把ANN—人工神經元網絡以及bp算法做一個簡單解釋。關於ANN的結構,我不再多說,網上有大量的學習資料,主要就是搞清一些名詞:輸入層/輸入神經元,輸出層/輸出神經元, 機器學習之支持向量機(一):支持向量機的公式推導根據 監督式 art 通用 利用 哪些 這就是 在線 方法 註:關於支持向量機系列文章是借鑒大神的神作,加以自己的理解寫成的;若對原作者有損請告知,我會及時處理。轉載請標明來源。 序: 我在支持向量機系列中主要講支持向量機的公式推導,第一部分講到推出拉格朗日對偶函數的對偶因 ps -ef |grep 輸出的具體含義終端 出行 apache 擁有 兩個 字符串 ps命令 系統啟動 查找 轉載: 比如:[root@localhost ~]# ps -ef | grep ApacheJetspeedroot 18887 18828 0 08:09 pts/0 00:00:0 文章閱讀:計算機體系-計算機將代碼編譯和持續運行過程中需要考慮的問題,以及具體的實現原理講解body ext ont 計算機 display convert pan 數據 borde 文章太棒,我無法理解和評價,備份一下。1、編程漫遊 - Mr.Riddler‘s Puzzle http://blog.mrriddler.com/2016/12/15/%E7%BC Harris Cornerarr 不變性 大小 偏移量 求和 尺度 找到 亮度 nbsp Harris Corner網上已經有很多的資料了,但它也是我讀研究生後讀的第一篇論文,對我有一種特別的意義。 這篇文章我想從幾個方面來講解Harris Corner,一是Harris Corner的思想,二是H 最速降線問題公式推導關系 工作 第一個 int sub dash calc quad 證明 以前對物理特別感興趣的時候就專門研究過一段時間的變分法,記得當時閱讀了一本十分不錯的書籍,其作者名挺有趣的—老大中先生的《變分法基礎》(真的很不錯的一本講變分法的書,有興趣的同學可以去看 機器學習 LR中的參數叠代公式推導——極大似然和梯度下降jpg blog 我們 應該 圖片 最大似然 gpo 機器學習實戰 pos 機器學習 LR中的參數叠代公式推導——極大似然和梯度下降 Logistic本質上是一個基於條件概率的判別模型(DiscriminativeModel)。 線性回歸 及 正則化 公式推導tail 損失函數 csdn .net net nbsp art 公式推導 模型 基礎公式: ?BA/?A = BT ?ATB/?A = B ?ATBA/?A = 2BA 模型函數: hθ(x) = xθ 無正則化損失函數: J(θ) = 1/2(Xθ-Y)2 點到超平面距離公式 推導idt ima .net || mage sub detail eight 技術 公式: d = |wx0 + b|/||w||2 推導: 參考文獻: https://blog.csdn.net/yutao03081/article/details/7 貝葉斯公式推導樣本 條件樣式 區別 str 假設 分享 們的 圖片 繼續 基本概念 樣本空間:{試驗所有可能結果}-->一個試驗所有可能結果的集合,用 Ω 表示。所以P(Ω) = 1 事件:樣本空間的一個子集。用A、B、C表示。 條件概率 其實 基於角色權限管理:rbac設計分析以及具體細節兩個文件 圖片 session creat 記得 ret back 現在 中間 權限管理---設計分析以及具體細節 說起權限我們大家都知道,不一樣的角色會有不一樣的權限。 比如就像學生管理系統一樣,管理員,老師,學生之間的權限都是不一樣的,那麽展示的頁面也是不一樣的。 |
