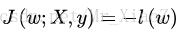L1、L2正則化來源推導

L1L2的推導可以從兩個角度：

• 帶約束條件的優化求解（拉格朗日乘子法）
• 貝葉斯學派的：最大後驗概率

1.1 基於約束條件的最優化

對於模型權重係數w的求解釋通過最小化目標函式實現的，也就是求解：

首先，模型的複雜度可以用VC來衡量。通常情況下，模型VC維與係數w的個數成線性關係：即：

w數量越多，VC越大，模型越複雜

為了限制模型的複雜度，我們要降低VC，自然的思路就是降低w的數量，即：

讓w向量中的一些元素為0或者說限制w中非零元素的個數。我們可以在原優化問題上加入一些優化條件：

其中約束條件中的||w||0是指L0範數，表示的是向量w中非零元素的個數，讓非零元素的個數小於某一個C，就能有效地控制模型中的非零元素的個數，但是這是一個NP問題，不好解，於是我們需要做一定的“鬆弛”。為了達到我們想要的效果（權重向量w中儘可能少的非零項），我們不再嚴格要求某些權重w為0，而是要求權重w向量中某些維度的非零引數儘可能接近於0，儘可能的小，這裡我們可以使用L1L2範數來代替L0範數，即：

注意哈：這裡使用L2範數的時候，為了後續處理（其實就是為了優化），可以對進行平方，只需要調整C的取值即可。

然後我們利用拉式乘子法求解：

其中這裡的是拉格朗日系數，>0，我們假設的最優解為，對拉格朗日函式求最小化等價於：

上面和

等價。所以我們這裡得到對L1L2正則化的第一種理解：

L1正則化  在原優化目標函式中增加約束條件

L2正則化  在原優化目標函式中增加約束條件

1.1 基於最大後驗概率估計

在最大似然估計中，是假設權重w是未知的引數，從而求得對數似然函式（取了log）：

從上式子可以看出：假設的不同概率分佈，就可以得到不同的模型。

若我們假設：

的高斯分佈，我們就可以帶入高斯分佈的概率密度函式：

上面的C為常數項，常數項和係數不影響我們求解的解，所以我們可以令

我們就得到了Linear Regursion的代價函式。

在最大化後驗概率估計中，我們將權重w看做隨機變數，也具有某種分佈，從而有：

同樣取對數：

可以看出來後驗概率函式為在似然函式的基礎上增加了logP(w)，P（w）的意義是對權重係數w的概率分佈的先驗假設，在收集到訓練樣本{X，y}後，則可根據w在{X，y}下的後驗概率對w進行修正，從而做出對w的更好地估計。

若假設的先驗分佈為0均值的高斯分佈，即

則有：

可以看到，在高斯分佈下

的效果等價於在代價函式中增加L2正則項。

若假設服從均值為0，引數為a的拉普拉斯分佈，即：

則有：

可以看到，在拉普拉斯分佈下logP(w)的效果等價在代價函式中增加L1正項。

故此，我們得到對於L1，L2正則化的第二種理解：

L1正則化可通過假設權重w的先驗分佈為拉普拉斯分佈，由最大後驗概率估計匯出。

L2正則化可通過假設權重w的先驗分佈為高斯分佈，由最大後驗概率估計匯出。