算術基本定理“質數分解唯一性的證明”:古典方法與現代方法
算術基本定理的最早證明是由歐幾里得給出的。
每一個比1大的自然數N只能有一種方式分解成質數的乘積。
推論:若一個質數p是乘積ab的因子,則p不是a的因子就是b的因子。
大於1的自然數必可寫成質數之積
用反證法:假設存在大於1的自然數不能寫成質數的乘積,把最小的那個稱為n。
自然數可以根據其可除性(是否能表示成兩個不是自身的自然數的乘積)分成3類:質數、合數和1。首先,按照定義,n 大於1。其次,n 不是質數,因為質\數p可以寫成質數乘積:p=p,這與假設不相符合。因此n只能是合數,但每個合數都可以分解成兩個嚴格小於自身而大於1的自然數的積。設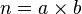 ,其中a 和b 都是介於1和n 之間的自然數,因此,按照n
,其中a 和b 都是介於1和n 之間的自然數,因此,按照n
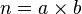 也可以寫成質數的乘積。由此產生矛盾。因此大於1的自然數必可寫成質數的乘積。
也可以寫成質數的乘積。由此產生矛盾。因此大於1的自然數必可寫成質數的乘積。
唯一性
歐幾里得《幾何原本》的證明方法
先證明推論:對應於《幾何原本》第7卷第30命題,設(7-30)
命題描述:以現在的數學語言,若質數p|ab,則不p|a就p|b
設c=ab;p為質數,若p量盡a,得證;若p量不盡a(即p不是a的因子),證明p量盡b即得證。
根據(7-29),因為p為質數,且p量不盡a,所以p、a互質。
用反證法證明如下:設p、a不互質,將有公因子m,因為m是a的因子,p不是a的因子,所以m不等於p,而m是p的因子,這是不可能的。
根據(7-定義15),c/p=t,得到c=pt,又c=ab,根據(7-19)得到p/a=b/t
根據(7-21),因為p、a互質,p、a是具有相同比的數對中最小的一對。
再根據(7-20),大小兩數a、p分別量盡具有同比的大小兩數t、b,所得的次數相同,即前項量盡前項、後項量盡後項,所以p量盡b,即得證。
最後一條定理(7-20)證明的難度較大,特證明如下:
命題:設a、b是與a/b有相同比的數對中最小的一對數,如果a/b=c/d,則a=(1/n)*c;b=(1/n)*d。
證明:因為a<c,所以a=(1/n)*c或者a=(m/n)*c,[1<m<n]
根據(7-13和定義20),若a=(m/n)*c,那麼也有b=(m/n)*d
這樣a、b均有(1/m)的部分
根據(7-12),(1/m)*a : (1/m)*b = a : b
但是(1/m)*a 、 (1/m)*b 分別小於 a 、b,這與假設矛盾,所以僅有a=(1/n)*c
根據(7-13和定義20),有a=(1/n)*c,b=(1/n)*d,故得證。
證明算術基本定理“質數分解唯一性”
命題:幾何原本描述,“如果一個數是被一些質數能量盡的最小者,那麼,除原來量盡它的質數外,任何另外的質數量不盡這個數。”
換句話說:一個數僅一種方法被分解為質因數之積。
設a是被質數b c d ... k的每一個整除的最小數,如果可能,假設a有一個不同與b c d ... k的質因數p,設a=p*m。根據(7-30),因為b c d ... k整除a,那麼它們必然整除兩因子p、m之一。而由假設,他們不整除p,所以他們必然整除小於a的數m,這與假設矛盾(假設a是最小的),因而a除b c d ... k外再無其他質因子。
現代證明方法,直接證明質數分解唯一性。
證明:反證法,設存在一個能分解為兩種根本不同的質數乘積的正整數,則其中必有一最小的(最小數原理),設m=p1p2...pr=q1q2...qs,從小到大排序。p1不等於q1,否則可消去,不滿足最小假設。設p1<q1。構造一整數m'=m-(p1q2...qs)=(p1p2...pr)-(p1q2...qs)=p1(p2...pr-q2...qs)
=(q1q2...qs)-(p1q2...qs)=(q1-p1)q2...qs
由於p1<q1,m'是一個正整數,且<m。因此m'的質數分解,除了因子次序外,必須是唯一的(m是最小數假設)。從上面表示式可看出,p1是m'的因子,再根據m'質數分解的唯一性得出(推論、用反證法很容易得到),p1必須是(q1-p1)或者q2...qs的因子,由於q都比p1大,這後一情形是不可能的,這樣就有某個整數h,使q1-p1=p1*h或q1=p1(h+1)。這表明p1是q1的一個因子,與q1是質數相矛盾。故得證。
