閔可夫斯基和

Tags：高階演算法

一、概述

學習此內容需一定計算幾何基礎，出門右拐：https://www.cnblogs.com/xzyxzy/p/10033130.html
官方定義：兩個圖形\(A,B\)的閔可夫斯基和\(C=\{a+b|a\in A,b\in B\}\)
通俗一點：從原點向圖形A內部的每一個點做向量，將圖形\(B\)沿每個向量移動，所有的最終位置的並便是閔可夫斯基和

由於博主太菜，本文只討論凸包的閔可夫斯基和
如下圖，粉色區域便是三角形和一個不規則四邊形的閔可夫斯基和

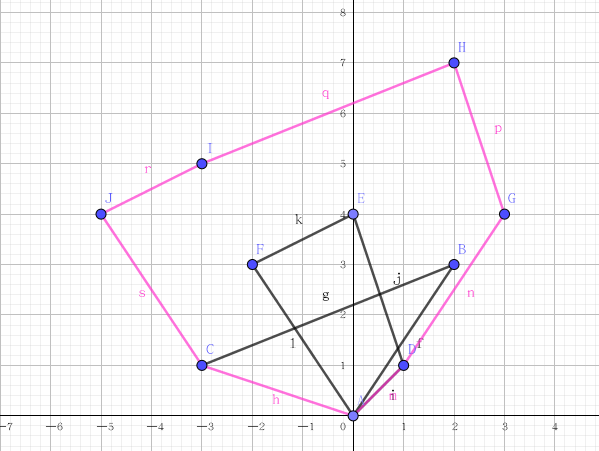
二、怎麼求

利用瞪眼法得，閔可夫斯基和的邊是由兩凸包構成的
也就是說把兩凸包的邊極角排序後直接順次連起來就是閔可夫斯基和

由於凸包的優美性質，直接歸併排序就好了
但是需要注意的是可能會有三點共線的情況，於是再扔過去重新求一次凸包就好了

三、應用舉例

題目

[JSOI2018]戰爭
兩個凸包\(A,B\)，移動\(B\)，問是否還有交點。\(n\le10^5,q\le10^5\)

正解

令\(a\in A,b\in B\)則移動向量\(w\)使得存在\(b+w=a\)
那麼\(w\)需要滿足\(w=a-b\)
構造閔可夫斯基和\(C=\{a+(-b)\}\)
在輸入\(B\)的時候橫縱座標都取反即可
餘下問題便是判斷輸入的移動向量是否在\(C\)內，計算幾何有講

樣例靚照

原圖

取反

閔可夫斯基和

用題目意思去理解閔可夫斯基和:
橙色的向量是\(B\)可以移動的範圍的邊界，也就是說在綠色框之內的向量都滿足條件
這些向量拖到以原點為起點，就是上面的閔可夫斯基和的粉色區域

程式碼

我覺得這題值這個黑色標籤
不是很好轉換，有點策不清

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#define ll long long
using namespace std;
const ll N=1e5+10;
struct Node
{
    ll x,y;
    Node operator - (Node A) {return (Node){x-A.x,y-A.y};}
    Node operator + (Node A) {return (Node){x+A.x,y+A.y};}
    ll operator * (Node A) const {return x*A.y-y*A.x;}
    ll len() const {return x*x+y*y;}
}A[N],C1[N],C2[N],s1[N],s2[N],bs;
ll cmp1(const Node&A,const Node&B) {return A.y<B.y||(A.y==B.y&&A.x<B.x);}
ll cmp2(const Node&A,const Node&B) {return A*B>0||(A*B==0&&A.len()<B.len());}
ll n,m,sta[N],top,q,tot;
void Convex(Node *A,ll &n)
{
    sort(A+1,A+n+1,cmp1);
    bs=A[1];sta[top=1]=1;
    for(ll i=1;i<=n;i++) A[i]=A[i]-bs;
    sort(A+2,A+n+1,cmp2);
    for(ll i=2;i<=n;sta[++top]=i,i++)
        while(top>=2&&(A[i]-A[sta[top-1]])*(A[sta[top]]-A[sta[top-1]])>=0) top--;
    for(ll i=1;i<=top;i++) A[i]=A[sta[i]]+bs;
    n=top;A[n+1]=A[1];
}
void Minkowski()
{
    for(ll i=1;i<n;i++) s1[i]=C1[i+1]-C1[i];s1[n]=C1[1]-C1[n];
    for(ll i=1;i<m;i++) s2[i]=C2[i+1]-C2[i];s2[m]=C2[1]-C2[m];
    A[tot=1]=C1[1]+C2[1];
    ll p1=1,p2=1;
    while(p1<=n&&p2<=m) ++tot,A[tot]=A[tot-1]+(s1[p1]*s2[p2]>=0?s1[p1++]:s2[p2++]);
    while(p1<=n) ++tot,A[tot]=A[tot-1]+s1[p1++];
    while(p2<=m) ++tot,A[tot]=A[tot-1]+s2[p2++];
}
ll in(Node a)
{
    if(a*A[1]>0||A[tot]*a>0) return 0;
    ll ps=lower_bound(A+1,A+tot+1,a,cmp2)-A-1;
    return (a-A[ps])*(A[ps%tot+1]-A[ps])<=0;
}
int main()
{
    cin>>n>>m>>q;
    for(ll i=1;i<=n;i++)
        scanf("%lld%lld",&C1[i].x,&C1[i].y);
    Convex(C1,n);
    for(ll i=1;i<=m;i++)
    {
        scanf("%lld%lld",&C2[i].x,&C2[i].y);
        C2[i].x=-C2[i].x;C2[i].y=-C2[i].y;
    }
    Convex(C2,m);
    Minkowski();
    Convex(A,tot);
    bs=A[1];for(ll i=tot;i>=1;i--) A[i]=A[i]-A[1];
    while(q--)
    {
        scanf("%lld%lld",&A[0].x,&A[0].y);
        printf("%lld\n",in(A[0]-bs));
    }
    return 0;
}