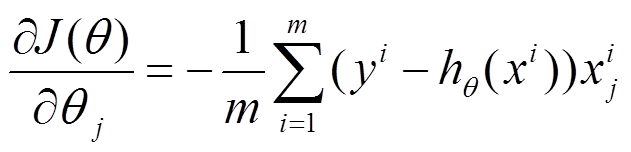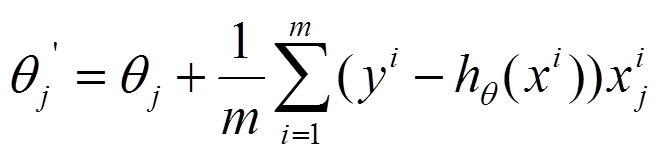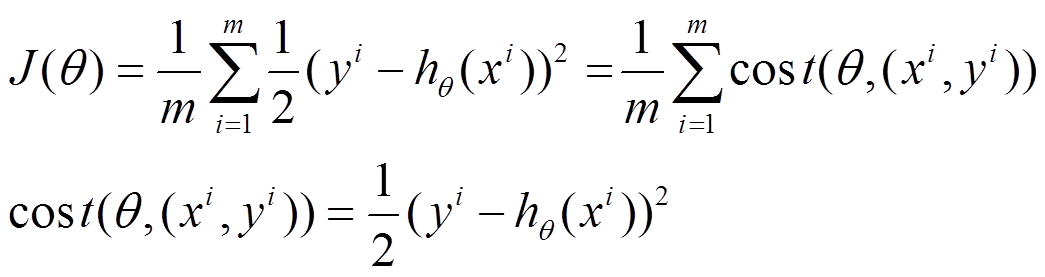在應用機器學習演算法時，我們通常採用梯度下降法來對採用的演算法進行訓練。其實，常用的梯度下降法還具體包含有三種不同的形式，它們也各自有著不同的優缺點。

　　下面我們以線性迴歸演算法來對三種梯度下降法進行比較。

　　一般線性迴歸函式的假設函式為：

h θ =∑ n j=0 θ j x j  hθ=∑j=0nθjxj

　　對應的能量函式（損失函式）形式為：

J train (θ)=1/(2m)∑ m i=1 (h θ (x (i) )−y (i) ) 2  Jtrain(θ)=1/(2m)∑i=1m(hθ(x(i))−y(i))2

　　下圖為一個二維引數（θ 0  θ0和θ 1  θ1）組對應能量函式的視覺化圖：

回到頂部

1. 批量梯度下降法BGD

 　　批量梯度下降法（Batch Gradient Descent，簡稱BGD）是梯度下降法最原始的形式，它的具體思路是在更新每一引數時都使用所有的樣本來進行更新，其數學形式如下：

　　(1) 對上述的能量函式求偏導：

　　(2) 由於是最小化風險函式，所以按照每個引數θ θ的梯度負方向來更新每個θ θ：

　　具體的虛擬碼形式為：

　　repeat{

　　　　　　

　　　　　　　　（for every j=0, ... , n）

　　}

　　從上面公式可以注意到，它得到的是一個全域性最優解，但是每迭代一步，都要用到訓練集所有的資料，如果樣本數目m m

很大，那麼可想而知這種方法的迭代速度！所以，這就引入了另外一種方法，隨機梯度下降。

　　優點：全域性最優解；易於並行實現；

　　缺點：當樣本數目很多時，訓練過程會很慢。

　　從迭代的次數上來看，BGD迭代的次數相對較少。其迭代的收斂曲線示意圖可以表示如下：

回到頂部

2. 隨機梯度下降法SGD

　　由於批量梯度下降法在更新每一個引數時，都需要所有的訓練樣本，所以訓練過程會隨著樣本數量的加大而變得異常的緩慢。隨機梯度下降法（Stochastic Gradient Descent，簡稱SGD）正是為了解決批量梯度下降法這一弊端而提出的。

　　將上面的能量函式寫為如下形式：

　　利用每個樣本的損失函式對θ

 θ求偏導得到對應的梯度，來更新θ θ：

　　具體的虛擬碼形式為：

　　1. Randomly shuffle dataset；

　　2. repeat{

　　　　for i=1, ... , m m{

　　　　　　

 　　　　　　(for j=0, ... , n n)

　　　　}

　　}

　　隨機梯度下降是通過每個樣本來迭代更新一次，如果樣本量很大的情況（例如幾十萬），那麼可能只用其中幾萬條或者幾千條的樣本，就已經將theta迭代到最優解了，對比上面的批量梯度下降，迭代一次需要用到十幾萬訓練樣本，一次迭代不可能最優，如果迭代10次的話就需要遍歷訓練樣本10次。但是，SGD伴隨的一個問題是噪音較BGD要多，使得SGD並不是每次迭代都向著整體最優化方向。

　　優點：訓練速度快；

　　缺點：準確度下降，並不是全域性最優；不易於並行實現。

　　從迭代的次數上來看，SGD迭代的次數較多，在解空間的搜尋過程看起來很盲目。其迭代的收斂曲線示意圖可以表示如下：

回到頂部

3. 小批量梯度下降法MBGD

　　有上述的兩種梯度下降法可以看出，其各自均有優缺點，那麼能不能在兩種方法的效能之間取得一個折衷呢？即，演算法的訓練過程比較快，而且也要保證最終引數訓練的準確率，而這正是小批量梯度下降法（Mini-batch Gradient Descent，簡稱MBGD）的初衷。

　　MBGD在每次更新引數時使用b個樣本（b一般為10），其具體的虛擬碼形式為：

　　Say b=10, m=1000.

　　Repeat{

　　　　for i=1, 11, 21, 31, ... , 991{

　　　　

　　　　(for every j=0, ... , n n)

　　　　}

　　}

4.具體實現描述

(1)線性迴歸的定義

(2)單變數線性迴歸

(3)cost function：評價線性迴歸是否擬合訓練集的方法 (4)梯度下降：解決線性迴歸的方法之一 (5)feature scaling：加快梯度下降執行速度的方法

(6)多變數線性迴歸

Linear Regression 注意一句話：多變數線性迴歸之前必須要Feature Scaling！
方法：線性迴歸屬於監督學習，因此方法和監督學習應該是一樣的，先給定一個訓練集，根據這個訓練集學習出一個線性函式，然後測試這個函式訓練的好不好（即此函式是否足夠擬合訓練集資料），挑選出最好的函式（cost function最小）即可； 注意： (1)因為是線性迴歸，所以學習到的函式為線性函式，即直線函式； (2)因為是單變數，因此只有一個x； 我們能夠給出單變數線性迴歸的模型： 我們常稱x為feature，h(x)為hypothesis； 從上面“方法”中，我們肯定有一個疑問，怎麼樣能夠看出線性函式擬合的好不好呢？ 我們需要使用到Cost Function（代價函式），代價函式越小，說明線性迴歸地越好（和訓練集擬合地越好），當然最小就是0，即完全擬合；

舉個實際的例子： 我們想要根據房子的大小，預測房子的價格，給定如下資料集： 根據以上的資料集畫在圖上，如下圖所示： 我們需要根據這些點擬合出一條直線，使得cost Function最小；

雖然我們現在還不知道Cost Function內部到底是什麼樣的，但是我們的目標是：給定輸入向量x，輸出向量y，theta向量，輸出Cost值； 以上我們對單變數線性迴歸的大致過程進行了描述； Cost Function Cost Function的用途：對假設的函式進行評價，cost function越小的函式，說明擬合訓練資料擬合的越好； 下圖詳細說明了當cost function為黑盒的時候，cost function 的作用；
但是我們肯定想知道cost Function的內部構造是什麼？因此我們下面給出公式： 其中： 表示向量x中的第i個元素； 表示向量y中的第i個元素； 表示已知的假設函式； m為訓練集的數量；

比如給定資料集(1,1)、(2,2)、(3,3) 則x = [1;2;3]，y = [1;2;3]     （此處的語法為Octave語言的語法，表示3*1的矩陣） 如果我們預測theta0 = 0，theta1 = 1，則h(x) = x，則cost function： J(0,1) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0； 如果我們預測theta0 = 0，theta1 = 0.5，則h(x) = 0.5x，則cost function： J(0,0.5) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0.58；

如果theta0 一直為 0， 則theta1與J的函式為： 如果有theta0與theta1都不固定，則theta0、theta1、J 的函式為：
當然我們也能夠用二維的圖來表示，即等高線圖；
注意：如果是線性迴歸，則costfunctionJ與的函式一定是碗狀的，即只有一個最小點； 以上我們講解了cost function 的定義、公式； Gradient Descent（梯度下降） 但是又一個問題引出了，雖然給定一個函式，我們能夠根據cost function知道這個函式擬合的好不好，但是畢竟函式有這麼多，總不可能一個一個試吧？ 因此我們引出了梯度下降：能夠找出cost function函式的最小值； 梯度下降原理：將函式比作一座山，我們站在某個山坡上，往四周看，從哪個方向向下走一小步，能夠下降的最快； 當然解決問題的方法有很多，梯度下降只是其中一個，還有一種方法叫Normal Equation； 方法： (1)先確定向下一步的步伐大小，我們稱為Learning rate； (2)任意給定一個初始值：； (3)確定一個向下的方向，並向下走預先規定的步伐，並更新； (4)當下降的高度小於某個定義的值，則停止下降； 演算法： 特點： (1)初始點不同，獲得的最小值也不同，因此梯度下降求得的只是區域性最小值； (2)越接近最小值時，下降速度越慢； 問題：如果初始值就在local minimum的位置，則會如何變化？ 答：因為已經在local minimum位置，所以derivative 肯定是0，因此不會變化； 如果取到一個正確的值，則cost function應該越來越小； 問題：怎麼取值？ 答：隨時觀察值，如果cost function變小了，則ok，反之，則再取一個更小的值； 下圖就詳細的說明了梯度下降的過程： 從上面的圖可以看出：初始點不同，獲得的最小值也不同，因此梯度下降求得的只是區域性最小值； 注意：下降的步伐大小非常重要，因為如果太小，則找到函式最小值的速度就很慢，如果太大，則可能會出現overshoot the minimum的現象； 下圖就是overshoot minimum現象： 如果Learning rate取值後發現J function 增長了，則需要減小Learning rate的值； Integrating with Gradient Descent & Linear Regression 梯度下降能夠求出一個函式的最小值； 線性迴歸需要求出，使得cost function的最小； 因此我們能夠對cost function運用梯度下降，即將梯度下降和線性迴歸進行整合，如下圖所示：
梯度下降是通過不停的迭代，而我們比較關注迭代的次數，因為這關係到梯度下降的執行速度，為了減少迭代次數，因此引入了Feature Scaling； Feature Scaling 此種方法應用於梯度下降，為了加快梯度下降的執行速度； 思想：將各個feature的值標準化，使得取值範圍大致都在-1<=x<=1之間； 常用的方法是Mean Normalization，即 或者： [X-mean(X)]/std(X);

舉個實際的例子， 有兩個Feature： (1)size，取值範圍0~2000； (2)#bedroom，取值範圍0~5； 則通過feature scaling後，

練習題 我們想要通過期中開始成績預測期末考試成績，我們希望得到的方程為：
給定以下訓練集：

midterm exam	(midterm exam)2	final exam
89	7921	96
72	5184	74
94	8836	87
69	4761	78

我們想對(midterm exam)^2進行feature scaling，則經過feature scaling後的值為多少？ max = 8836,min=4761,mean=6675.5，則x=(4761-6675.5)/(8836-4761) = -0.47； 多變數線性迴歸 前面我們只介紹了單變數的線性迴歸，即只有一個輸入變數，現實世界不可能這麼簡單，因此此處我們要介紹多變數的線性迴歸； 舉個例子： 房價其實由很多因素決定，比如size、number of bedrooms、number of floors、age of home等，這裡我們假設房價由4個因素決定，如下圖所示：

我們前面定義過單變數線性迴歸的模型： 這裡我們可以定義出多變數線性迴歸的模型： Cost function如下： 如果我們要用梯度下降解決多變數的線性迴歸，則我們還是可以用傳統的梯度下降演算法進行計算：
總練習題： 1.我們想要根據一個學生第一年的成績預測第二年的成績，x為第一年得到A的數量，y為第二年得到A的數量，給定以下資料集：

x	y
3	4
2	1
4	3
0	1

(1)訓練集的個數是多少？  4個； (2)J(0,1)的結果是多少？ J(0,1) = 1/(2*4)*[(3-4)^2+(2-1)^2+(4-3)^2+(0-1)^2] = 1/8*(1+1+1+1) = 1/2 = 0.5； 我們也可以通過vectorization的方法快速算出J(0,1)：
回到頂部