如何通俗地解釋 PID 引數整定?
阿新 • • 發佈:2019-01-07
作者:忘川孤帆
連結:https://www.zhihu.com/question/23088613/answer/23942834
來源:知乎
著作權歸作者所有,轉載請聯絡作者獲得授權。
由於PID屬於無模型控制,調節三個環節的引數會產生什麼影響根據控制物件的不同也會有很大差別。你提到的這些結論其實都是根據經驗總結出來的。
既然你說是從來沒有接觸過PID,那我就舉例儘量說明一下PID控制是怎麼一回事。
1)假設我們面對的系統是一個簡單的水箱的液位,要從空箱開始注水直到達到某個高度,而你能控制的變數是注水籠頭的開關大小。那麼這個簡單的數學模型就是

對於這個簡單的系統,我們甚至只需要一個比例環節

就能將其控制住。
說白了,也就是水箱液位離預定高度遠的時候就開大點,離的近的時候就開小點,隨著液位逐步接近預定高度逐漸關掉水龍頭。
此時,
<img src="https://pic2.zhimg.com/1bf9717813a61536a354d075804f58c1_b.jpg" data-rawheight="420" data-rawwidth="561" class="origin_image zh-lightbox-thumb" width="561" data-original="https://pic2.zhimg.com/1bf9717813a61536a354d075804f58c1_r.jpg">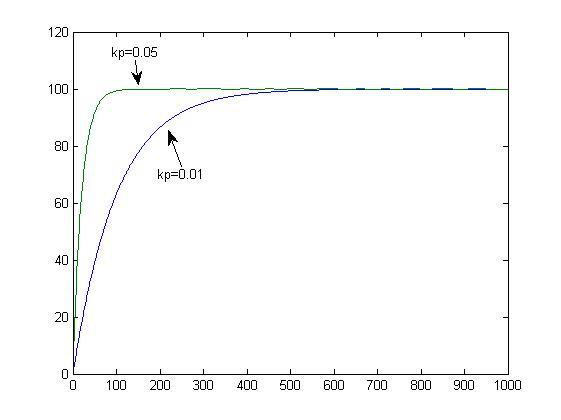
2)假設咱們這個水箱不僅僅是裝水的容器了,還需要持續穩定的給使用者供水。
那這個系統的數學模型就需要增加一項:
 ,這裡這個
,這裡這個 是個正的常數。
是個正的常數。
這時候我們發現如果控制器只有一個比例環節,那麼當系統穩定,也就是 的時候,恰好
的時候,恰好 。
。 在系統穩定時不為0,液位離我們想要的高度總是差那麼一點,這也就是所謂的穩態誤差,或者叫靜差。
在系統穩定時不為0,液位離我們想要的高度總是差那麼一點,這也就是所謂的穩態誤差,或者叫靜差。
這時候 是固定的,那麼當然
是固定的,那麼當然 越大,
越大, 就越小。這也就是所謂的增大比例係數P在有靜差的情況下有利於減小靜差。如下圖:
就越小。這也就是所謂的增大比例係數P在有靜差的情況下有利於減小靜差。如下圖:
<img src="https://pic2.zhimg.com/a51fc3b348843992aa4344afdf95c6c9_b.jpg" data-rawheight="420" data-rawwidth="561" class="origin_image zh-lightbox-thumb" width="561" data-original="https://pic2.zhimg.com/a51fc3b348843992aa4344afdf95c6c9_r.jpg">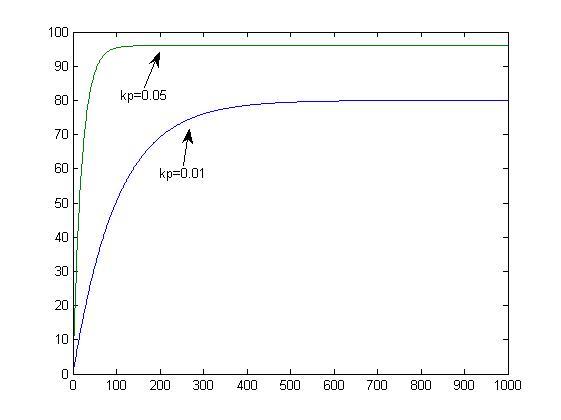
3) 從上面的式子 大家可以看出來,
大家可以看出來, 再大那也只是個分母,不可能把
再大那也只是個分母,不可能把 變成0的。老是調不到預定位置老闆是會罵人的,這可咋辦?
變成0的。老是調不到預定位置老闆是會罵人的,這可咋辦?
然後有人就想到,第二小節裡頭那個水箱跟第一小節的相比,不就是多了一個漏水的窟窿麼。它漏多少我給它補多少,那不就成了第一小節裡的簡單系統了麼。靠誰補呢?積分環節這時候就派上用場了。
我們把之前的控制器變成比例環節+積分環節:
積分環節的意義就相當於你增加了一個水龍頭,這個水龍頭的開關規則是水位比預定高度低就一直往大了擰,比預定高度高就往小了擰。如果漏水速度不變,那麼總有一天這個水龍頭出水的速度恰好跟漏水的速度相等了,系統就和第一小節的那個一樣了。那時,靜差就沒有了。這就是所謂的積分環節可以消除系統靜差。
4)啥叫積分時間常數呢?一般PID控制裡,表示積分環節敏感度的那個係數 , 這個
, 這個 就是積分時間常數。從這個式子我們可以看出,積分時間常數越大,積分環節係數就越小,積分環節就越不敏感(也就是第二個水龍頭越細)。
就是積分時間常數。從這個式子我們可以看出,積分時間常數越大,積分環節係數就越小,積分環節就越不敏感(也就是第二個水龍頭越細)。
當咱們只有一個比例環節的水龍頭注水的時候,是不會注水注多的,因為離得越近水龍頭關的越小啊。
但是當咱們用倆水龍頭注水的時候,在沒到預定高度前第二個積分環節的水龍頭可以一直在往大了擰的,那當到達預定高度的時候它恰好擰到最大,自然而然就會注水注多了。而多出去的這部分水就叫做“超調”。第二個水龍頭越粗,多注的水就會越多,它調到恰好等於漏水速度的時間就會越快,但同時會多更多波折。
於是,老師告訴我們增大積分時間I有利於減小超調,減小振盪,使系統的穩定性增加,但是系統靜差消除時間變長。如下圖:
<img src="https://pic4.zhimg.com/7d20a7bb08b55a6e4003011ecde23623_b.jpg" data-rawheight="420" data-rawwidth="561" class="origin_image zh-lightbox-thumb" width="561" data-original="https://pic4.zhimg.com/7d20a7bb08b55a6e4003011ecde23623_r.jpg">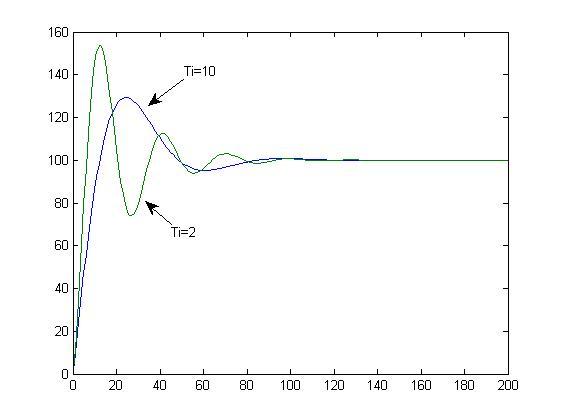
5)接下來我們來看點有意思的東西。還是上面這個系統,假如我們選用相同的積分時間常數,但是選擇不同的比例係數會如何呢?
<img src="https://pic1.zhimg.com/a224805640cbca84abe63225e4106758_b.jpg" data-rawheight="420" data-rawwidth="561" class="origin_image zh-lightbox-thumb" width="561" data-original="https://pic1.zhimg.com/a224805640cbca84abe63225e4106758_r.jpg">看到上面這幅圖,一些記性好的童鞋可能就有疑問了。因為老師明明說過”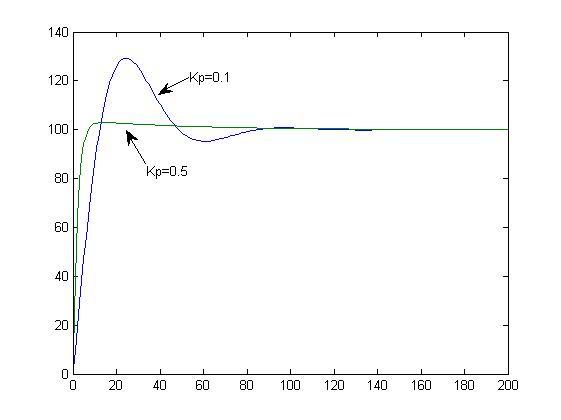 看到上面這幅圖,一些記性好的童鞋可能就有疑問了。因為老師明明說過”過大的比例係數會使系統有比較大的超調,併產生振盪,使穩定性變壞“,但是上面這幅圖裡怎麼比例大的反而超調小呢?
看到上面這幅圖,一些記性好的童鞋可能就有疑問了。因為老師明明說過”過大的比例係數會使系統有比較大的超調,併產生振盪,使穩定性變壞“,但是上面這幅圖裡怎麼比例大的反而超調小呢?
其實上面這幅圖很好解釋,小節4裡我們說明了PI控制器超調出現原因是積分這個水龍頭在到達目標液位時也恰好開到了最大。而比例這個水龍頭越粗,那麼它在超出目標液位時對超調的抑制也就越明顯。
這裡,我想再強調的是:PID引數整定的結論是根據普遍經驗總結的,但是針對某個具體的系統不一定完全適用。
6) 在上面的系統中,我們假設使用者用水的固定的一個值,但是實際情況中使用者的用水量往往是變化的。假如我們的系統是 呢?
呢?
來分析一下:
我們的控制目標是讓 ,系統誤差的定義是:
,系統誤差的定義是: ;
;
那麼誤差狀態方程就是
上面我們設定的控制目標是個常數,所以 ;
;
那麼
從上面這個式子我們可以看出,當 時,
時, 不再變化,而
不再變化,而 是始終變化的。
是始終變化的。
那麼此時 不恆為零,也就是說
不恆為零,也就是說 不恆為零。
不恆為零。
也就是說,當 變成
變成 的時候,
的時候, 就不再是系統的穩定平衡點了,經典意義上系統不再穩定。
就不再是系統的穩定平衡點了,經典意義上系統不再穩定。
7)這裡加一個微分環節D變成PID控制會不會讓系統重新穩定呢?
當加入微分環節,
那麼
對於任意 (
( ),微分環節都讓
),微分環節都讓 的變化減慢了,這也就是
的變化減慢了,這也就是
“微分環節主要作用是在響應過程中抑制偏差向任何方向的變化”
“微分常數不能過大,否則會使響應過程提前制動,延長調節時間”
而至於“微分環節會降低系統的抗干擾性能”,更多指的是大多數細微測量噪聲造成的 很小,但瞬時的
很小,但瞬時的 較大,微分環節相對於PI環節更容易收到這些細微噪聲的影響。
較大,微分環節相對於PI環節更容易收到這些細微噪聲的影響。
但是,
無論如何選取微分引數 ,PID控制都不能使系統穩定。
,PID控制都不能使系統穩定。
從這裡,我們可以看到PID控制的侷限。
——————————————————————————————————————————
微分環節想了很久,最後還是覺得想到的例子都不夠清楚準確,還是用式子更順手一些。
希望大家不要死記口訣,多用所學到的控制理論來針對具體問題具體分析。
——————————————————————————————————————————
2015-9-26:謝 @大頭菠蘿 指正。第7小節那個結論的準確說法應該是“微分環節會提高系統抗擾動能力,降低系統抗噪聲能力”。
連結:https://www.zhihu.com/question/23088613/answer/23942834
來源:知乎
著作權歸作者所有,轉載請聯絡作者獲得授權。
由於PID屬於無模型控制,調節三個環節的引數會產生什麼影響根據控制物件的不同也會有很大差別。你提到的這些結論其實都是根據經驗總結出來的。
既然你說是從來沒有接觸過PID,那我就舉例儘量說明一下PID控制是怎麼一回事。
1)假設我們面對的系統是一個簡單的水箱的液位,要從空箱開始注水直到達到某個高度,而你能控制的變數是注水籠頭的開關大小。那麼這個簡單的數學模型就是
對於這個簡單的系統,我們甚至只需要一個比例環節
就能將其控制住。
說白了,也就是水箱液位離預定高度遠的時候就開大點,離的近的時候就開小點,隨著液位逐步接近預定高度逐漸關掉水龍頭。
此時,
<img src="https://pic2.zhimg.com/1bf9717813a61536a354d075804f58c1_b.jpg" data-rawheight="420" data-rawwidth="561" class="origin_image zh-lightbox-thumb" width="561" data-original="https://pic2.zhimg.com/1bf9717813a61536a354d075804f58c1_r.jpg">

2)假設咱們這個水箱不僅僅是裝水的容器了,還需要持續穩定的給使用者供水。
那這個系統的數學模型就需要增加一項:
這時候我們發現如果控制器只有一個比例環節,那麼當系統穩定,也就是
這時候
<img src="https://pic2.zhimg.com/a51fc3b348843992aa4344afdf95c6c9_b.jpg" data-rawheight="420" data-rawwidth="561" class="origin_image zh-lightbox-thumb" width="561" data-original="https://pic2.zhimg.com/a51fc3b348843992aa4344afdf95c6c9_r.jpg">

3) 從上面的式子
然後有人就想到,第二小節裡頭那個水箱跟第一小節的相比,不就是多了一個漏水的窟窿麼。它漏多少我給它補多少,那不就成了第一小節裡的簡單系統了麼。靠誰補呢?積分環節這時候就派上用場了。
我們把之前的控制器變成比例環節+積分環節:
積分環節的意義就相當於你增加了一個水龍頭,這個水龍頭的開關規則是水位比預定高度低就一直往大了擰,比預定高度高就往小了擰。如果漏水速度不變,那麼總有一天這個水龍頭出水的速度恰好跟漏水的速度相等了,系統就和第一小節的那個一樣了。那時,靜差就沒有了。這就是所謂的積分環節可以消除系統靜差。
4)啥叫積分時間常數呢?一般PID控制裡,表示積分環節敏感度的那個係數
當咱們只有一個比例環節的水龍頭注水的時候,是不會注水注多的,因為離得越近水龍頭關的越小啊。
但是當咱們用倆水龍頭注水的時候,在沒到預定高度前第二個積分環節的水龍頭可以一直在往大了擰的,那當到達預定高度的時候它恰好擰到最大,自然而然就會注水注多了。而多出去的這部分水就叫做“超調”。第二個水龍頭越粗,多注的水就會越多,它調到恰好等於漏水速度的時間就會越快,但同時會多更多波折。
於是,老師告訴我們增大積分時間I有利於減小超調,減小振盪,使系統的穩定性增加,但是系統靜差消除時間變長。如下圖:
<img src="https://pic4.zhimg.com/7d20a7bb08b55a6e4003011ecde23623_b.jpg" data-rawheight="420" data-rawwidth="561" class="origin_image zh-lightbox-thumb" width="561" data-original="https://pic4.zhimg.com/7d20a7bb08b55a6e4003011ecde23623_r.jpg">

5)接下來我們來看點有意思的東西。還是上面這個系統,假如我們選用相同的積分時間常數,但是選擇不同的比例係數會如何呢?
<img src="https://pic1.zhimg.com/a224805640cbca84abe63225e4106758_b.jpg" data-rawheight="420" data-rawwidth="561" class="origin_image zh-lightbox-thumb" width="561" data-original="https://pic1.zhimg.com/a224805640cbca84abe63225e4106758_r.jpg">看到上面這幅圖,一些記性好的童鞋可能就有疑問了。因為老師明明說過”
 看到上面這幅圖,一些記性好的童鞋可能就有疑問了。因為老師明明說過”過大的比例係數會使系統有比較大的超調,併產生振盪,使穩定性變壞“,但是上面這幅圖裡怎麼比例大的反而超調小呢?
看到上面這幅圖,一些記性好的童鞋可能就有疑問了。因為老師明明說過”過大的比例係數會使系統有比較大的超調,併產生振盪,使穩定性變壞“,但是上面這幅圖裡怎麼比例大的反而超調小呢?其實上面這幅圖很好解釋,小節4裡我們說明了PI控制器超調出現原因是積分這個水龍頭在到達目標液位時也恰好開到了最大。而比例這個水龍頭越粗,那麼它在超出目標液位時對超調的抑制也就越明顯。
這裡,我想再強調的是:PID引數整定的結論是根據普遍經驗總結的,但是針對某個具體的系統不一定完全適用。
6) 在上面的系統中,我們假設使用者用水的固定的一個值,但是實際情況中使用者的用水量往往是變化的。假如我們的系統是
來分析一下:
我們的控制目標是讓
那麼誤差狀態方程就是
上面我們設定的控制目標是個常數,所以
那麼
從上面這個式子我們可以看出,當
那麼此時
也就是說,當
7)這裡加一個微分環節D變成PID控制會不會讓系統重新穩定呢?
當加入微分環節,
那麼
對於任意
“微分環節主要作用是在響應過程中抑制偏差向任何方向的變化”
“微分常數不能過大,否則會使響應過程提前制動,延長調節時間”
而至於“微分環節會降低系統的抗干擾性能”,更多指的是大多數細微測量噪聲造成的
但是,
無論如何選取微分引數
從這裡,我們可以看到PID控制的侷限。
——————————————————————————————————————————
微分環節想了很久,最後還是覺得想到的例子都不夠清楚準確,還是用式子更順手一些。
希望大家不要死記口訣,多用所學到的控制理論來針對具體問題具體分析。
——————————————————————————————————————————
2015-9-26:謝 @大頭菠蘿 指正。第7小節那個結論的準確說法應該是“微分環節會提高系統抗擾動能力,降低系統抗噪聲能力”。
