決策樹的部分理解

• 決策樹

  • 是表示基於特徵對例項進行分類的樹形結構

  • 從給定的訓練資料集中，依據特徵選擇的準則，遞迴的選擇最優劃分特徵，並根據此特徵將訓練資料進行分割，使得各子資料集有一個更好的分類的過程

• 決策樹演算法的三要素：

  • 特徵選擇

  • 決策樹生成

  • 決策樹剪枝（暫時沒接觸到）

• 關於決策樹生成：

  • 決策樹的生成過程就是使用滿足劃分準則的特徵不斷的將資料集劃分為純度更高，不確定性更小的子集的過程

  • 對於當前資料集D的每一次的劃分，都希望根據某特徵劃分之後的各子集的純度更高，不確定性更小

• 而如何度量劃分資料集前後的資料集的純度以及不確定性呢？

  • 答案是：特徵選擇準則

    • 比如：資訊增益，資訊增益率，基尼指數

  • 特徵選擇準則的目的

    • 使用某特徵對資料集進行劃分之後，各資料子集的純度要比劃分前的資料集D的純度高（不確定性要比劃分前資料集D的不確定性低）

• 我們使用的特徵選擇準則是：基尼指數（CART演算法---分類樹）

  • 基尼指數（基尼不純度），表示在樣本集合中一個隨機選中的樣本被分錯的概率

  • PS： 基尼指數越小表示集合中被選中的樣本被分錯的概率越小，也就是說集合的純度越高，反之，集合越不純

  • 即：

    • 基尼指數（基尼不純度） = 樣本被選中的概率 * 樣本分錯的概率

  • 書中公式：

    • 

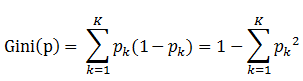
    • 說明：

    • 1、Pk表示選中的樣本屬於k類別的概率，則這個樣本被分錯的概率是（1 - Pk）

    • 2、樣本集合有K個類別，一個隨機選中的樣本可以屬於這K個類別中的任意一個，因而就K個類別的概率進行相加

  • 比如樣本集合D的Gini指數

    • 假設集合中有K個類別，則：

    • 

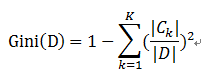
• January 8, 2019