傳送門

題面：

Werewolf

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 559    Accepted Submission(s): 123

 

Problem Description

"The Werewolves" is a popular card game among young people.In the basic game, there are 2 different groups: the werewolves and the villagers.

Each player will debate a player they think is a werewolf or not. 

Their words are like "Player x is a werewolf." or "Player x is a villager.".

What we know is :

1. Villager won't lie.

2. Werewolf may lie. 

Of cause we only consider those situations which obey the two rules above. 

It is guaranteed that input data exist at least one situation which obey the two rules above.

Now we can judge every player into 3 types :

1. A player which can only be villager among all situations, 

2. A player which can only be werewolf among all situations.

3. A player which can be villager among some situations, while can be werewolf in others situations.

You just need to print out the number of type-1 players and the number of type-2 players. 

No player will talk about himself.

Input

The first line of the input gives the number of test cases T.Then T test cases follow.

The first line of each test case contains an integer N,indicating the number of players.

Then follows N lines,i-th line contains an integer x and a string S,indicating the i-th players tell you,"Player x is a S."

limits:

1≤T≤10

1≤N≤100,000

1≤x≤N

S∈ {"villager"."werewolf"}

Output

For each test case,print the number of type-1 players and the number of type-2 players in one line, separated by white space.

Sample Input

1 2 2 werewolf 1 werewolf

Sample Output

0 0

Source

題目描述：

    有n個人在玩狼人殺，每個人有兩種身份，狼或者村民，村民必須要將真話，而狼可能講假話。現在每個人都會說出一個除了自己外的一個人身份，現在問你有多少個人確定是村民，有多少個人確定是狼人。

題目分析：

    因為題目不排斥所有玩家都是狼人的情況（這一點都不符合遊戲規則好吧），因此題目中所有的人說的所有的話均有可能是假的。因此我們完全無法確定是否有人是村民。但是存在一定是狼人的情況。

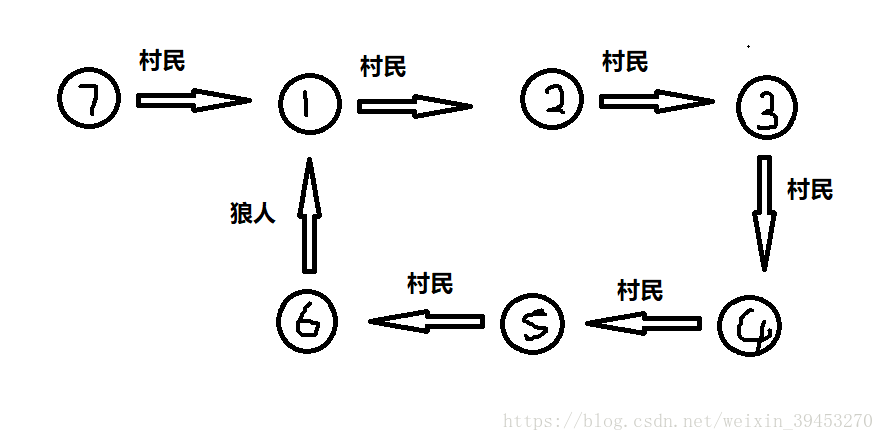
    當出現一種類似下圖的情況：

    當我們發現有連續個點是有村民的邊，如點1，點2，點3，點4，點5，點6；而這些個連續的其中一個點（如圖中的點6）有一條狼人邊連到了這些個連續的其他的點（如上圖練到了點1）。

    此時，我們用反證法可以證明，倘若1號點是村民，則根據村民不會說謊的性質可以判斷出1到6號點全是村民，而根據村民不會說謊的性質，只能證明出1號點必為狼人。此時我們同時也可以發現，倘若1號點是狼人，則根據狼人會說謊的性質可知，指向1號點的村民邊則必定是狼人。

    因此我們的演算法雛形就初步顯現出來了。

    因為我們要維護一些連續的村民點，因此我們可以用一個並查集進行維護。我們可以將村民邊上的兩個點不斷的用並查集去合併，而當我們遍歷狼邊的時候，倘若我們發現狼邊上的兩個點都在一個集合中，則說明必定滿足上述的情況，則我們不斷遍歷這條狼人邊所指向的那個結點（如上圖的1號點），判斷有多少條指向它的村民邊即可。（此處我們可以將村民邊反向建立，這樣可以讓我們高效的查詢）。

程式碼：

#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
typedef pair<int,int>PLL;
vector<int>human[maxn];
vector<PLL>wolf;
int Far[maxn];
int n;
void init(){//初始化
    for(int i=1;i<=n;i++){
        Far[i]=i;
    }
    wolf.clear();
    for(int i=0;i<=n;i++){
        human[i].clear();
    }
}
int Find_F(int x){//並查集找爸爸
    if(Far[x]==x) return x;
    else return Far[x]=Find_F(Far[x]);
}
void unit(int x,int y){//並查集合並
    x=Find_F(x);
    y=Find_F(y);
    if(x==y) return ;
    else Far[x]=y;
}
bool same(int x,int y){//判斷是否在一個集合
    return Find_F(x)==Find_F(y);
}
int ans=0;
void dfs(int x){//dfs找指向該點的村民邊
    int len=human[x].size();
    for(int i=0;i<len;i++){
        ans++;
        dfs(human[x][i]);
    }
}
int main()
{
    int t;
    cin>>t;
    while(t--){
        scanf("%d",&n);
        init();
        for(int i=1;i<=n;i++){
            char str[20];
            int op;
            scanf("%d%s",&op,str);
            if(str[0]=='v'){
                human[op].push_back(i);//反向建邊
                unit(op,i);
            }
            else{
                wolf.push_back(make_pair(i,op));
            }
        }
        ans=0;
        int sz=wolf.size();
        for(int i=0;i<sz;i++){
            int from=wolf[i].first;
            int to=wolf[i].second;
            if(same(from,to)){
                ans++;
                dfs(to);
            }
        }
        cout<<"0 "<<ans<<endl;
    }
}