哈夫曼編碼的實現
哈夫曼編碼雖然在acm上用到的似乎很少,但其經常作為一種基礎演算法出現在計算機類的書籍上。
而我對哈夫曼編碼的理解也僅僅侷限在其用於編碼領域,可以提高資料傳輸效率,或者是用於壓縮檔案?這些可能並不準確,我沒有細細的去查證。
哈夫曼編碼可以通過構建哈夫曼樹來得到。
舉例
我們用一個簡單的例子,來簡單描述下哈夫曼編碼是什麼?有什麼好處?
場景:X地區需要向Y地區傳送一些文字,兩地之間通過電纜(或者通過電報)連線,要求用最少的二進位制流傳遞資訊:ABACDAAB
可以看到該資訊中一共出現4個A,2個B,C、D各1個
1. 如果用常見的二進位制形式編碼,那麼A:00,B:01,C:10,D:11;資訊轉二進位制流為:0001001011000001,一共是16位。
2. 如果用哈夫曼編碼,則其的一種為A:1,B:01,C:000,D:001;資訊轉二進位制流為:10110000011101,一共是14位,比普通的少2位。
這時,我們可能就明白了哈夫曼編碼不就是頻率出現越高,其編碼越短嗎?
我們嘗試這樣來賦值,A:0,B:1,C:01,D:10;二進位制流為:0100110001,這個只有10位,比哈夫曼還少呢!
上面的說法似乎有道理,但是我們忽略了哈夫曼的用途可能是資訊傳輸和壓縮。當我們把編碼規則和二進位制流告訴接收方時,他們需要把這些二進位制流還原為看得懂的資訊。普通編碼和哈夫曼編碼都可以順利還原,而第三種則不可能還原,0100....到底是ABAA....還是CAA....呢?
所以哈夫曼編碼必須是字首碼,而且還是最優字首碼
因此,必須達到以上兩點構造出的編碼才是哈夫曼碼。
求解
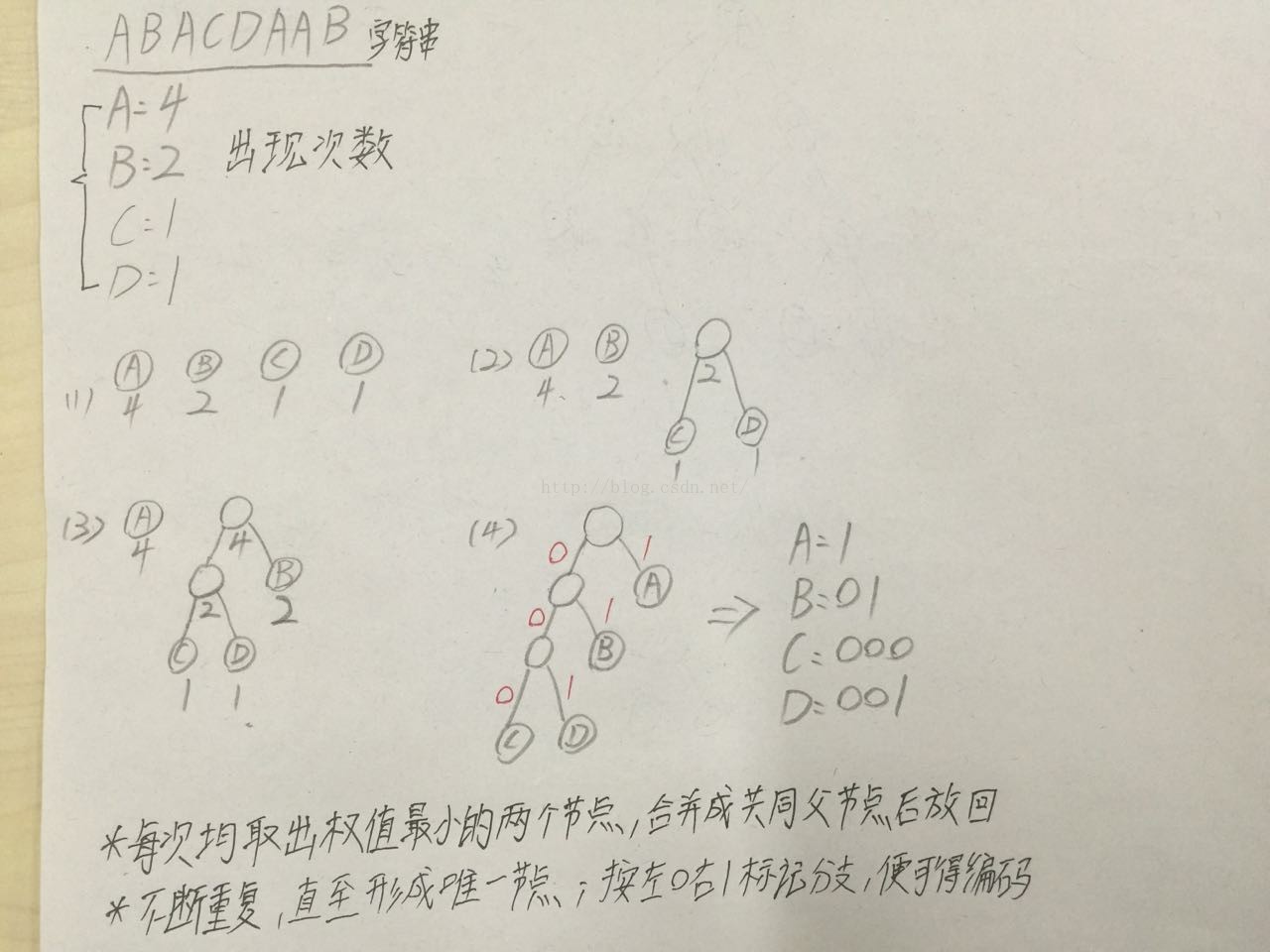
下面我們還是通過這個例子,簡單來看看當獲得ABACDAAB時,如何通過構建哈夫曼樹求每個字元的哈夫曼編碼:
步驟一:獲得每個字元出現的次數作為該字元節點的權值;
步驟二:每次選取權值最小的兩個節點,合併成有共同的父節點後放回;不斷重複,直至只剩下一個節點;此時按照左分支為0,右分支為1進行編碼;
具體的過程詳見下圖:
程式碼的實現
步驟一可以通過雜湊遍歷來獲得每個字母的出現次數;
步驟二可用二叉連結串列模擬建樹來實現;
步驟二中每次從集合中彈出兩權值最小的節點合併為同一父節點後還要放回,顯然需要在普通佇列上加段每次插入後都排序的程式碼;如果自己造輪子想必還要費點時間,好在C++標準庫提供了“優先佇列
下面我們來看下具體的程式碼:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<queue>
using namespace std;
typedef struct node{
char ch; //儲存該節點表示的字元,只有葉子節點用的到
int val; //記錄該節點的權值
struct node *self,*left,*right; //三個指標,分別用於記錄自己的地址,左孩子的地址和右孩子的地址
friend bool operator <(const node &a,const node &b) //運算子過載,定義優先佇列的比較結構
{
return a.val>b.val; //這裡是權值小的優先出佇列
}
}node;
priority_queue<node> p; //定義優先佇列
char res[30]; //用於記錄哈夫曼編碼
void dfs(node *root,int level) //列印字元和對應的哈夫曼編碼
{
if(root->left==root->right) //葉子節點的左孩子地址一定等於右孩子地址,且一定都為NULL;葉子節點記錄有字元
{
if(level==0) //“AAAAA”這種只有一字元的情況
{
res[0]='0';
level++;
}
res[level]='\0'; //字元陣列以'\0'結束
printf("%c=>%s\n",root->ch,res);
}
else
{
res[level]='0'; //左分支為0
dfs(root->left,level+1);
res[level]='1'; //右分支為1
dfs(root->right,level+1);
}
}
void huffman(int *hash) //構建哈夫曼樹
{
node *root,fir,sec;
for(int i=0;i<26;i++) //程式只能處理全為大寫英文字元的資訊串,故雜湊也只有26個
{
if(!hash[i]) //對應字母在text中未出現
continue;
root=(node *)malloc(sizeof(node)); //開闢節點
root->self=root; //記錄自己的地址,方便父節點連線自己
root->left=root->right=NULL; //該節點是葉子節點,左右孩子地址均為NULL
root->ch='A'+i; //記錄該節點表示的字元
root->val=hash[i]; //記錄該字元的權值
p.push(*root); //將該節點壓入優先佇列
}
//下面迴圈模擬建樹過程,每次取出兩個最小的節點合併後重新壓入佇列
//當佇列中剩餘節點數量為1時,哈夫曼樹構建完成
while(p.size()>1)
{
fir=p.top();p.pop(); //取出最小的節點
sec=p.top();p.pop(); //取出次小的節點
root=(node *)malloc(sizeof(node)); //構建新節點,將其作為fir,sec的父節點
root->self=root; //記錄自己的地址,方便該節點的父節點連線
root->left=fir.self; //記錄左孩子節點地址
root->right=sec.self; //記錄右孩子節點地址
root->val=fir.val+sec.val;//該節點權值為兩孩子權值之和
p.push(*root); //將新節點壓入佇列
}
fir=p.top();p.pop(); //彈出哈夫曼樹的根節點
dfs(fir.self,0); //輸出葉子節點記錄的字元和對應的哈夫曼編碼
}
int main()
{
char text[100];
int hash[30];
memset(hash,0,sizeof(hash)); //雜湊陣列初始化全為0
scanf("%s",text); //讀入資訊串text
for(int i=0;text[i]!='\0';i++)//通過雜湊求每個字元的出現次數
{
hash[text[i]-'A']++; //程式假設執行的全為英文大寫字母
}
huffman(hash);
return 0;
}因為在其被合併時,需要將自己的地址傳遞給父節點的孩子指標。而我們每次壓入佇列的是一個節點變數,並不是該節點的地址,所以必須有域記錄該節點的地址。那如果我們改一下優先佇列的定義,讓其中儲存的從變數改成地址呢?
priority_queue<struct node *> p;
p.push(root);
答案仍然是否定的,優先佇列的比較函式過載時不能接受地址,原因詳見“liuzhanchen1987”的部落格,感謝這位博主的分享。
演示程式
之前我有用VC6寫過兩個小程式,分別用哈夫曼編碼實現編碼傳送資訊和解碼還原資訊。
如果有需要可以“點選下載”,程式目前還只能傳輸大寫英文字元,數字和少量標點;如果要傳輸更多的字元,擴大雜湊陣列的長度即可。
程式只提供原始碼和執行的截圖,見諒^_^