基於Graham掃描線演算法的更加強大的凸包演算法——Melkman演算法
大家好,這裡是蒟蒻霞客,thewalker88
今天我來給大家講解一種OI中很少有人使用,然而在我看來比常用的Graham掃描線演算法更為強大的演算法——Mlekman演算法
為了學習這個新演算法,你需要如下前置技能:
1),會計算幾何基礎,尤其是叉積
2),掌握Graham掃描線演算法求凸包
如果你不會如上前置技能,網上各路神犇的關於此的講解很多,如果能夠先點亮這些前置技能,理解這篇部落格無疑會更加輕鬆
那麼,如果現在你們已經點亮了上述前置技能……
我們開始吧!!!
對於點集求凸包,Graham掃描線是可以在O(nlogn)的時間內完美解決的,而且很容易可以知道點集求凸包的時間複雜度下界是O(nlogn)。
但是,如果是求簡單多邊形的凸包呢?
簡單多邊形:沒有自交邊的多邊形即為簡單多邊形(凸多邊形,凹多邊形皆可)
問題:
平面上有一個簡單多邊形,沿著多邊形的邊,按照逆時針的順序給出多邊形的頂點的座標,要求你求出此多邊形的凸包。
如果你還記得對於點集的凸包我們是如何解決的的話,我們先是將點按照某種順序排序(水平序或極角序),再從某個一定在凸包上的點上的開始掃描。
但是我們注意到,對於按順序給出的簡單多邊形上的點,他們本身就帶著一個序!!!(感性理解一下)
因此,我們求簡單多邊形的凸包,只需要從某個必在凸包上的點開始用Graham掃描線計算一圈,就可以求出此多邊形的凸包了。。。。。
看起來是這樣,其實並不是
因為Graham 無法處理如下圖的簡單多邊形!
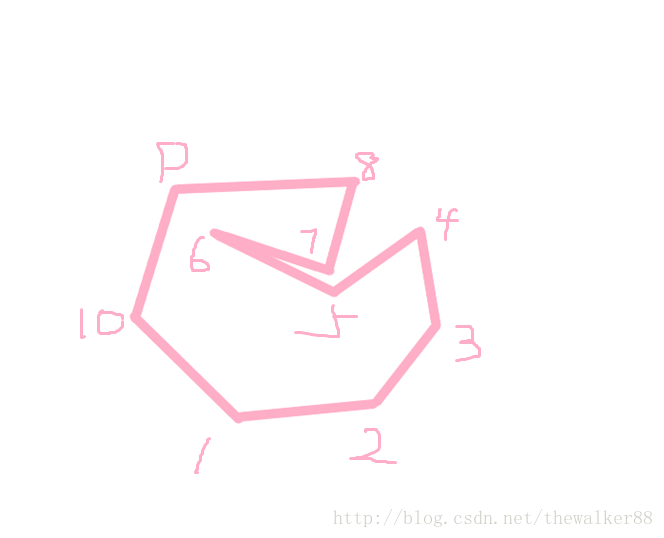
對於這個多邊形,我們從一號頂點開始掃描,從1一直到6都是沒有問題的,此時棧裡面從底到頂的頂點編號是1、2、3、4、6
此時考慮點7,我們驚訝的發現,線段46到線段67是逆時針旋轉的,這意味著點7不會造成彈棧 ,最後,我們求出的凸包將是,下圖中的紅色部分
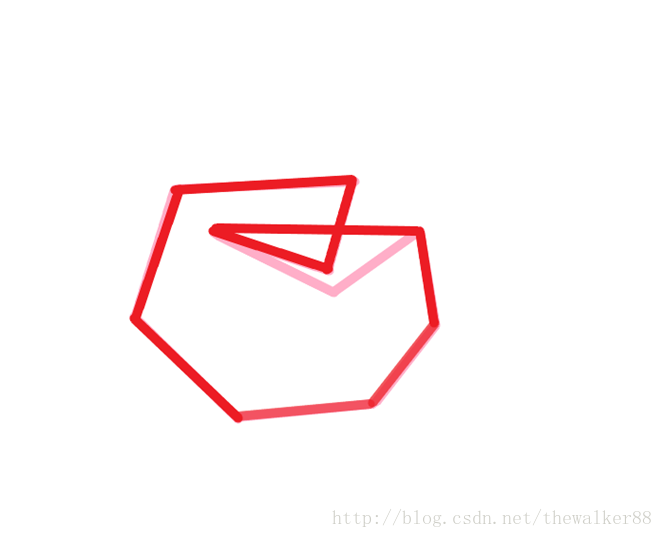
可見,Graham對於此類多邊形求得的凸包將是一個複雜多邊形,顯然錯誤
因此,我們只能將其像處理點集一樣,先排序再搞。
然而,這樣不僅沒利用上簡單多邊形自帶的序,而且複雜度還是O(nlogn)的,很不好
因此,我現在來介紹一種由Melkman在1987年發明的,可以在O(n)的時間複雜度下求出正確的,簡單多邊形的凸包的Melkman演算法
這個演算法是基於Graham掃描線演算法的,他們的大體思路相同,但是不同之處在於,Graham使用一個棧來維護凸包,而Melkman使用一個雙頭佇列來維護凸包,每次不僅僅維護佇列頭的凸性,也維護佇列尾的凸性,因此,它得到每時每刻都包含當前考慮過的所有的點的凸包
下面我們模擬一下
對於一個n個點的多邊形,我們開一個大小為2*n的deque(即雙頭佇列),設bot為佇列尾,top為佇列頭,bot初始值為n-1,top初始值為n
我們把點1從前插入佇列,同時top++,接下來,由於佇列裡只有一個點1,我們可以直接把2從佇列頭插入和把2從佇列尾插入注意,從現在起每時每刻,佇列頭和佇列尾的點總是同一個,也就是當前凸包裡的最後考慮的點
接下來我們插入點3
我們說過,要在佇列頭和佇列尾都維護凸性,如果佇列頭不是凸的,在佇列頭彈棧(top–),如果佇列尾不是凸的,我們在佇列尾彈棧(bot++),我們寫程式的時候,在佇列頭維護一下,然後入棧,之後在佇列尾維護一下,然後入棧,所以最後,我們的佇列會是3 1 2 3或者3 2 1 3
這是頭三個點
我們現在來考慮點4,我們看,佇列頭和佇列正數第二個點所連成的直線,佇列尾和佇列倒數第二個點所連成的直線,以及剩下的凸包上的邊們,會把平面分為5個部分,看圖
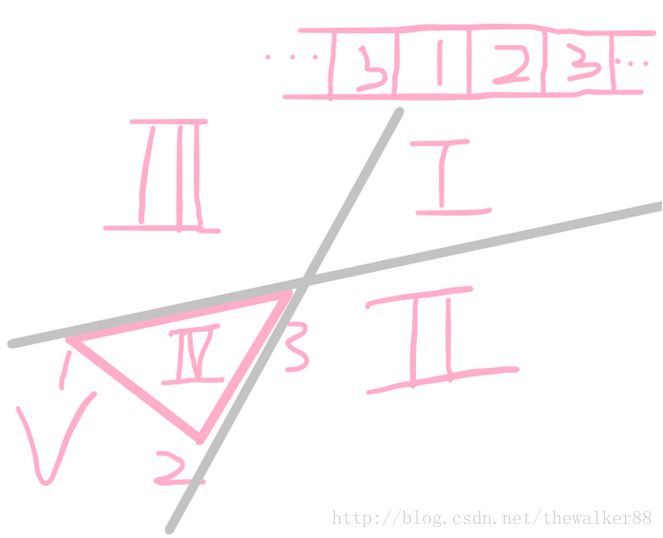
如果第四個點落在區域II,說明對列頭不合法了,在佇列頭彈棧,如果在區域III,我們要在佇列尾進行維護,如果在區域I,我們要把佇列的頭和尾一起進行維護,如果在區域IV說明這個點是當前所求得的凸包內部的點,明顯對答案沒有貢獻,我們此時直接忽略這個點去看第五個點(上次用Graham跑凸包時的錯誤可被此情況排除)
那麼,如果點落在區域V呢???
並不會落在區域V!
因為我們是個簡單多邊形,如果在區域V有點,則必然產生自交邊,這是違背簡單多邊形的定義的。
如此進行下去,直到我們將所有的點考慮一遍,此時bot+1到top-1就是凸包上的點
時間複雜度很明顯是線性的,因為每個點最多進棧出棧一次
而且此演算法還是個線上演算法,可以隨時接收新的點,並且我最開始塞入佇列中的點不必非得在凸包上,相比之下,這個演算法比Graham妙得多
來看一下蒟蒻醜到不行的程式碼
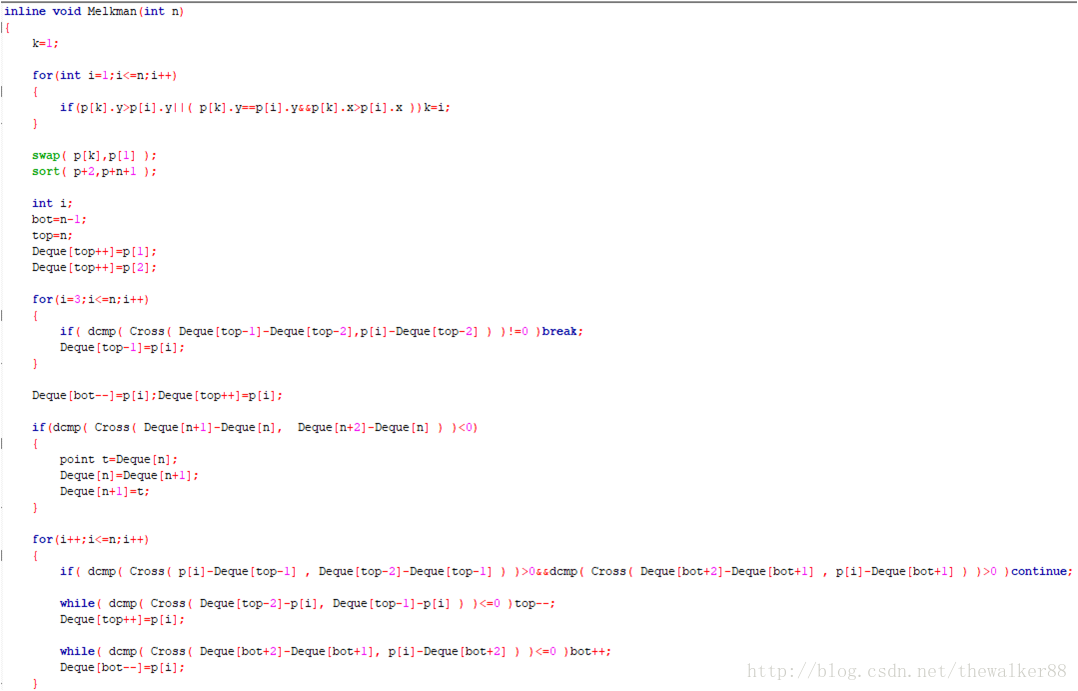
實現細節:判斷在什麼區域時,只需要先排除IV區,接著佇列頭佇列尾分別判斷即可,無需細究究竟是什麼區域
那麼就是這樣,通過對此部落格的閱讀,您:
1),明白了求簡單多邊形凸包時Graham錯誤的原因
2),學會了目前最優的凸包演算法——Melkman演算法
3),明白了這個部落格創作者是個蒟蒻
如果您第二條收穫並沒有,建議您再仔細看看,因為我的部落格可能是最詳細的講授Melkman演算法的了
就是這樣希望您有收穫
我的QQ號是1145101354 ,歡迎大家加我來討論問題(請註明來自CSDN)
以上
(還不快誇我可愛QwQ
注:本文中貼出的程式碼與文中的程式碼實現並不是完全一樣
此程式碼是先將點1,2入隊,如果1,2,3時逆時針的,則直接入3(結束後佇列為:”3,1,2,3“),否則將1,2調換位置,然後入3(結束後佇列為:”3,2,1,3“)
然而18.03.09晚在我正在給東北的眾神犇口胡的時候,神犇Camouflager 提出,2也如同之後的點一樣前後都加入佇列,然後再慢慢彈棧,這樣對正確性沒有影響,而且程式碼似乎能好寫點,經過思考覺得神犇就是神犇,說的話挺有道理,因此本文中對演算法描述的時候採用了Camouflager的想法。這是與原論文不一樣的地方
