機器學習---迴歸預測---向量、矩陣求導
梯度
對於 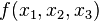 ,可以通過下面的向量方程來表示梯度:
,可以通過下面的向量方程來表示梯度:
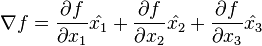

佈局約定
向量關於向量的導數:即 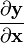 ,如果分子y 是m維的,而分母x 是n維的:
,如果分子y 是m維的,而分母x 是n維的:
- 分子佈局(Jacobian 形式),即按照y列向量和x橫向量. (得到m×n矩陣:橫向y1/x1 y1/x2 y1/x3 縱向y1/x1 y2/x1 y3/x1)
- 分母佈局(Hessian 形式)(梯度),即按照y橫向量和x列向量,是Jacobian形式的轉置。(得到n×m矩陣:橫向y1/x1 y2/x1 y3/x1 縱向y1/x1 y1/x2 y1/x3
分子佈局下的向量求導(分母佈局=分子佈局轉置)
標量/向量(橫):
![\frac{\partial y}{\partial \mathbf{x}} =\left[\frac{\partial y}{\partial x_1}\frac{\partial y}{\partial x_2}\cdots\frac{\partial y}{\partial x_n}\right].](https://upload.wikimedia.org/math/0/5/8/058a849a9a78fddbf1e59bcc4fa1f47c.png)
向量(列)/標量:
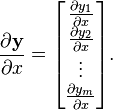
向量/向量:
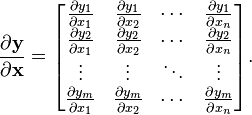
標量/矩陣:
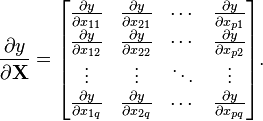
矩陣/標量:
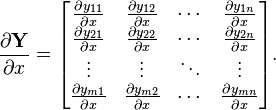
性質
- 鏈式規則:
- 乘積規則:
- 求和規則:
相關推薦
機器學習---迴歸預測---向量、矩陣求導
梯度 對於 ,可以通過下面的向量方程來表示梯度: 佈局約定 向量關於向量的導數:即 ,如果分子y 是m維的,而分母x 是n維的: 分子佈局(Jacobian 形式),即按照y列向量和x橫向量. (得到m×n矩陣:橫向y1/x1 y1/x2 y1/x3
機器學習線性迴歸中,用矩陣求導方法求最小二乘法的方法
在我們推導最小二乘法的時候,Andrew提供了兩種方法,一個是梯度下降法則,另一個是矩陣求導法則。後來在《機器學習實戰裡》面看線性迴歸程式碼的時候,裡面就是用了矩陣求導法則。要看懂矩陣求導法則,是需要一些矩陣論的知識的,還記得今年夏天我在苦逼地到處求矩陣論地速成
3 Spark機器學習 spark MLlib 矩陣向量、矩陣運算Breeze庫-1
機器學習裡矩陣是必不可少的,無論Python、Java能做機器學習的語言,都會提供比較優質的矩陣庫。 spark mllib中提供的矩陣庫是Breeze,可以簡單看看Breeze庫的情況。 ScalaNLP是一套機器學習和數值計算的庫,主要是關於科學計算、機器學習和自
機器學習實戰——預測數值型資料:迴歸 實現記錄
關於利用資料集繪圖建立模型 >>> import regression >>> xArr, yArr= regression.loadDataSet('ex0.txt') >>> ws= regression.standRegres(xAr
吳恩達機器學習中協方差矩陣的向量表示推導
一、多維隨機變數的協方差矩陣 對多維隨機變數列向量,我們往往需要計算各維度之間的協方差,這樣協方差就組成了一個n×nn×n的矩陣,稱為協方差矩陣。協方差矩陣是一個對角矩陣,對角線上的元素是各維度上隨機變數的方差。 我們定義協方差為, 矩陣內的元素為 協方差矩陣為
CSDN機器學習筆記一 概述、線性迴歸
一、課程知識點 講師:唐宇迪 本次課程 1.系列課程環境配置 2.機器學習概述 3.線性迴歸演算法原理推導 4.邏輯迴歸演算法原理 5.最優化問題求解 6.案例實戰梯度下降 一、機器學習處理問題過程及常用庫 1. 機
機器學習之區域性加權、嶺迴歸和前向逐步迴歸
都說萬事開頭難,可一旦開頭,就是全新的狀態,就有可能收穫自己未曾預料到的成果。記錄是為了更好的監督、理解和推進,學習過程中用到的資料集和程式碼都將上傳到github 迴歸是對一個或多個自變數和因變數之間的關係進行建模,求解的一種統計方法,之前的部落格中總結了線上性迴歸中使用最小二乘法推導最優引
機器學習之支援向量機迴歸(機器學習技法)
核函式山脊迴歸Represent Theorem表達理論就是指如果一個模型是帶有L2正則化的線性模型,那麼它在最佳化的時候的權重引數值W*將能夠用Z空間的資料的線性組合來表示。它的推論就是L2的正則化線性模型能夠核函式化如下圖所示:現在我們的目標就是用核函式的方式去解決迴歸問
機器學習常見的矩陣求導總結
常見求導公式 1.∂(xTAx)∂x=(AT+A)x,x為向量 2.∂tr(XTX)∂X=2X,X為矩陣 3. ∂tr(XTAX)∂X=(A+AT)X,X為向量 4. ∂tr(ATB)∂A=B,X為向量 5. ∂tr(X)X=I,X為向量 6. ∂
機器學習中向量函式的求導問題
在機器學習演算法的學習過程中,經常會遇到對向量函式的求導問題,閱讀一些文章之後,對於機器學習演算法中經常用到的這些求導問題做一些說明,方便在不明白的時候可以進行查詢。 (一)對標量求導1)向量對
【機器學習筆記】二、 Regression迴歸
一、基礎 這裡面,輸入變數x有兩個,一個是居住面積(living area),一個是房間數目(bedrooms)。 所以x 是一個二維向量。表示第i組資料中的居住面積(living area)。表示第i組資料中的房間數目。 我們假設輸入和輸出呈線性關係,那麼便有下面的公式
機器學習---支持向量機(SVM)
行處理 off 距離 又是 分類器 libs 自己的 cos 一個 非常久之前就學了SVM,總認為不就是找到中間那條線嘛,但有些地方模棱兩可,真正編程的時候又是一團漿糊。參數任意試驗,毫無章法。既然又又一次學到了這一章節,那就要把之前沒有搞懂的地方都整明確,嗯~
numpy數組、向量、矩陣運算
bool zip github 詳細 spa one num 切片 rod 可以來我的Github看原文,歡迎交流。 https://github.com/AsuraDong/Blog/blob/master/Articles/%E6%9C%BA%E5%99%A8%E5%A
python大戰機器學習——支持向量機
高斯 方法 技術 擴展 -1 ges 分時 nts 提高 支持向量機(Support Vector Machine,SVM)的基本模型是定義在特征空間上間隔最大的線性分類器。它是一種二類分類模型,當采用了核技巧之後,支持向量機可以用於非線性分類。 1)線性可分支持向
4. 向量、矩陣和數組
函數類 pic 官方 peter 適合 開始 長度 索引數組 mes 4.1 向量 4.1.1 序列 除了使用冒號運算符之外,R還支持其他函數創建更為通用的序列。其中,seq函數最為常見,能以許多不同的方式指定序列。在平常使用中針對不同的場景,我們有以下三類函數可供使用
機器學習-支持向量機算法實現與實例程序
training mage 線性 opts 線性可分 tps gist 填充 rain 一. SMO算法基礎 支持向量就是離分隔超平面最近的那些點。分隔超平面是將數據集分開來的決策邊界。 支持向量機將向量映射到一個更高維的空間裏,在這個空間裏建立有一個最大間隔超
線性迴歸 矩陣求導
一種方便區別是概率還是似然的方法是,根據定義,"誰誰誰的概率"中誰誰誰只能是概率空間中的事件,換句話說,我們只能說,事件(發生)的概率是多少多少(因為事件具有概率結構從而刻畫隨機性,所以才能談概率);而"誰誰誰的似然"中的誰誰誰只能是引數,比如說,引數等於 時的似然是多少
機器學習系列之偏差、方差與交叉驗證
一、偏差與方差 在機器學習中,我們用訓練資料集去訓練(學習)一個model(模型),通常的做法是定義一個Loss function(誤差函式),通過將這個Loss(或者叫error)的最小化過程,來提高模型的效能(performance)。然而我們學習一個模型的目的是為了解決實際的問題(或者說是
[機器學習]svm支援向量機介紹
1 什麼是支援向量機 支援向量機是一種分類器,之所以稱為 機 是因為它會產生一個二值決策結果,即它是一個決策機。 Support Vector Machine, 一個普通的SVM就是一條直線罷了,用來完美劃分linearly separable的兩類。但這又不是一條
機器學習之支援向量機(四)
引言: SVM是一種常見的分類器,在很長一段時間起到了統治地位。而目前來講SVM依然是一種非常好用的分類器,在處理少量資料的時候有非常出色的表現。SVM是一個非常常見的分類器,在真正瞭解他的原理之前我們多多少少都有接觸過他。本文將會詳細的介紹SVM的原理、目標以及計算過程和演算法步驟。我們針對線性可分資





