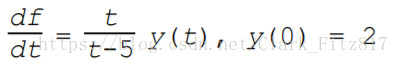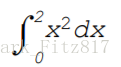《matlab揭祕》求極限,導數,微分方程,積分筆記
第六章基本符號演算和微分方程
主要內容:
- 計算極限
- 求導數
- 求常微分方程(ODE)的解析解和數值解
- 求積分
計算極限
命令一般形式:limit(f,m,direction)
f : 需要計算極限的表示式,f中的變數必須使用syms定義,否則會因為無法識別而報錯
m: 指明計算f趨近於m時的極限,如果不填,預設是0
direction: 是一個字串,值有’left’,'right’和不填 ,分別代表求左極限,右極限,和預設求極限
計算導數
命令:diff(f,n)
f : 需要求的原函式 ,必須將變數宣告為 syms
n : 要求的幾階導
解常微分方程的解析解
命令一般形式:dsolve(f1,f2,…fn,‘cond1’,‘cond2’,…‘condn’)
fn : 一個字串, 內容是方程的表示式 ,
f1到fn 表示求解方程組
condn : 字串,內容是初始條件的表示式
例:
dsolve(‘Dy = y*t/(t-5)’,‘y(0)=2’);
二階導用 D2表示
注意 預設地,dsolve 使用 t 作為獨立變數。我們可以告訴它使用其它變數——在命令列的 末尾附帶上我們要使用的獨立變數
解常微分方程的數值解
這個需要說明解析解和數值解的區別:
解析解意思是解可以用表示式具體的寫出來,而數值解是隻能得到點對,無法得到解析式,因為不是所有的常微分方程都有解析解,大部分只能得到數值解
解數值解用到的命令是
ode23()和ode45()兩種
這兩個函式都使用(龍格-庫塔)法來數值解,區別是ode45比ode23階數更高,對應的ode45的精度也比ode23高
兩個函式的呼叫方式完全相同
[t,y] = ode23(‘func_name’, [start_time, end_time], y(0))
func_name 是在單獨的.m檔案中定義的方程函式
[start_time, end_time] 是求解區間
y(0)是初值
如果要求解二階的常微分方程,需要將二階方程通過換元轉換為一階方程組
% 例如 求方程 y'' + 16y = sin(4.3t)當 y(0) = y'(0) = 0 時的解。 % 換元:令x1 = y; % x2 = y'; % 定義微分方程函式 %建立陣列儲存資料 xdot = zerot(2,1); % 列方程組 xdot(2) = sin(4.3*t)-16*x(1); xdot(1) = x(2); % 呼叫函式 [t,x] = ode23('fun',[0 2*PI],[0,0]); % x(:,1) 是 y 的解 % x(:,2) 是 y' 的解 plot(t,x(:,1)); % 畫出數值解的影象
求積分
一般形式的命令:
int(f,v)
f 需要求積分的表示式,可以是字串,也可以是變量表達式
v(可選) 是指定的變數,如果表示式中有多個變元,沒有指定時會預設其中的一個符號為變數
注意matlab給出的積分省略了常數部分,在寫結果時需要加上
求定積分
一般形式的命令:
int(f,v,end,start)
f : 同求積分
v: 同求積分
end 定積分的上界
start 定積分的下界
注意這裡的上下界的順序
求多重積分
int()命令可以進行巢狀,即在單重積分的基礎上巢狀int命令就可以求多重積分
求數值積分
數值積分是指已知了數值,但是沒有關係式
使用命令: trapz(x,y)
例:計算
x = linspace(0,2,10); % 將區間[0,2]分成10等份
f = x.^2;
trapz(x,f); % 就得到了積分結果
% 相對於int()求定積分存在一定的誤差
求正交積分
使用命令quad()和quadl()都可以,使用方法同int()
美化表示式的顯示
命令:pretty(f) 可以將表示式展示成日常手寫的形式,方便觀察
f: 需要美化的表示式
設定多個圖的屬性
設定屬性的命令是 set(h,key,value)
h 是一個指標,指向圖的例項
那麼如何獲得圖的物件呢?
就需要使用 get(gca,'children')命令了
返回的是一個數組,元素是每一個圖物件,這樣就可以指定每一個圖的屬性了,比如顏色,線條等